Le Funzioni: Definizione e Caratteristiche

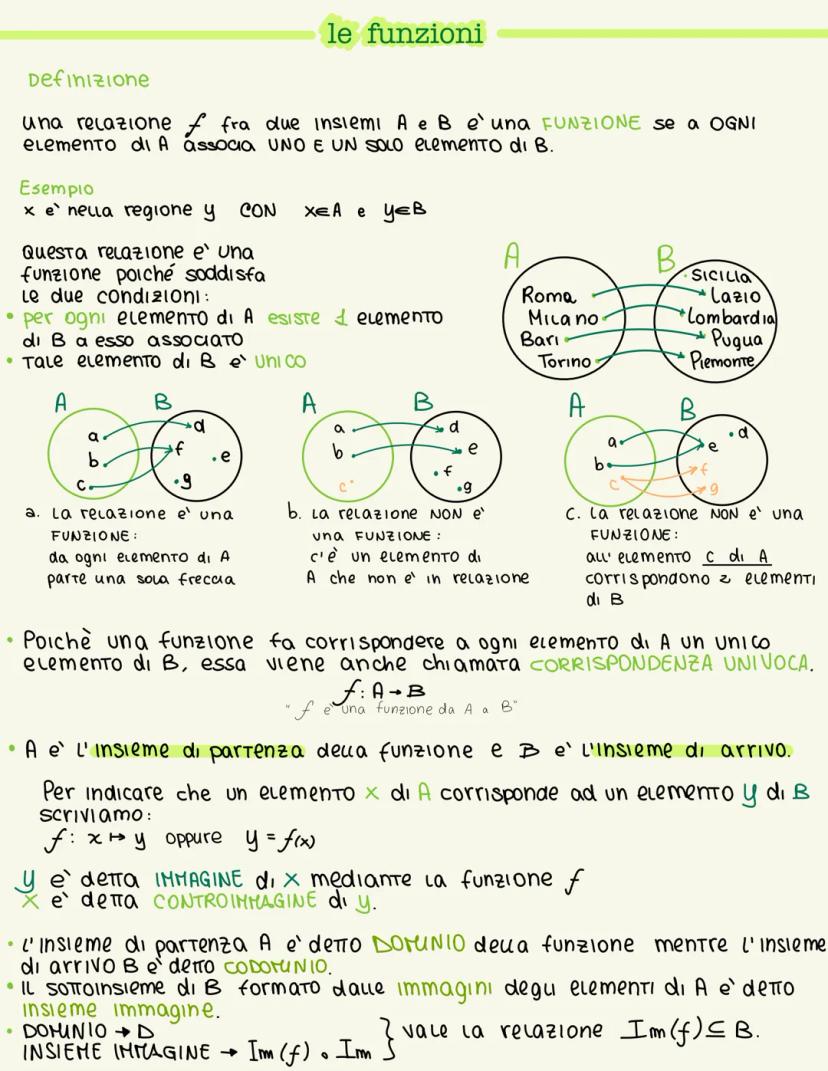
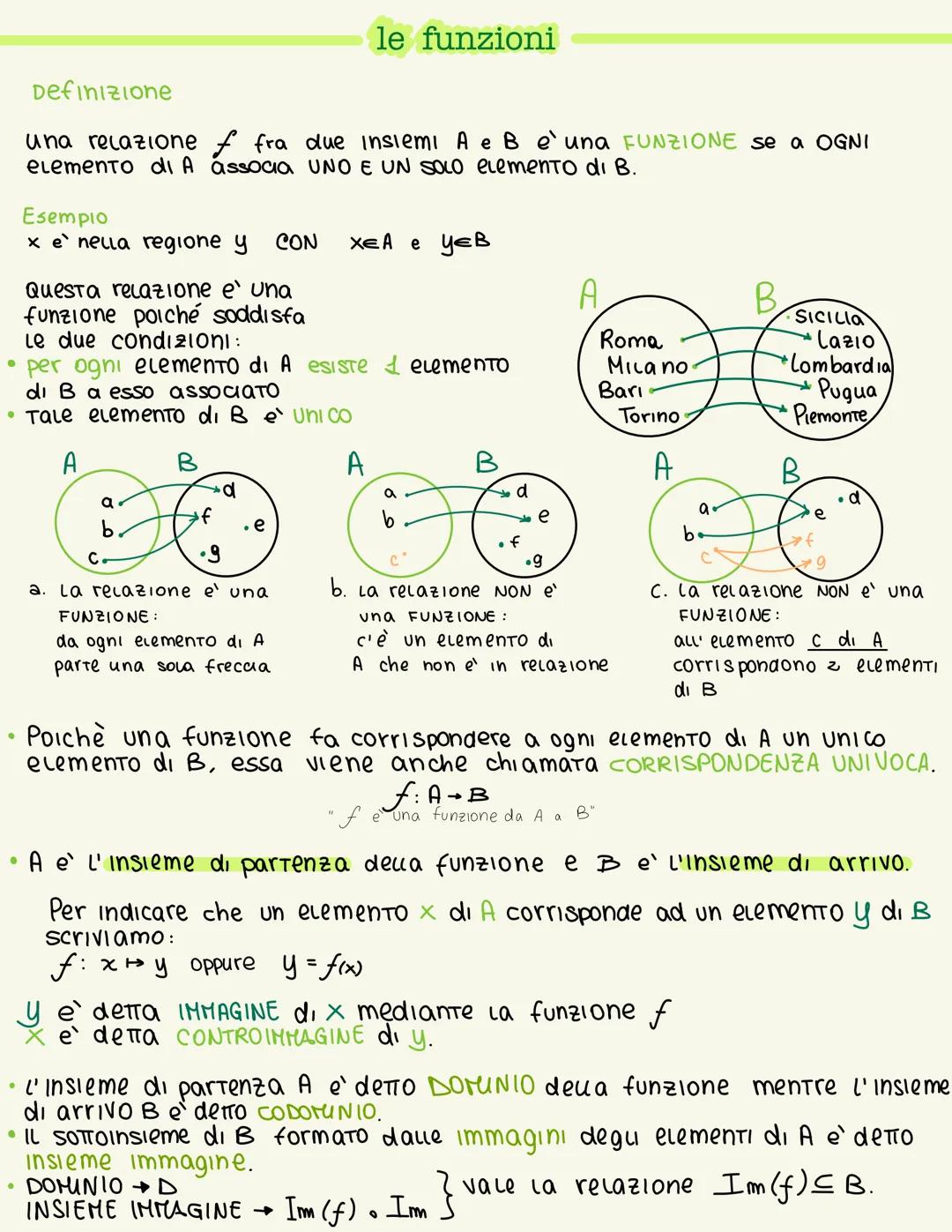
Una funzione è una relazione speciale tra due insiemi A e B che rispetta due regole ferree: ogni elemento di A deve essere collegato a uno e un solo elemento di B. Niente di più, niente di meno!

Pensa all'esempio delle città e delle loro regioni: Roma appartiene solo al Lazio, Milano solo alla Lombardia. Ogni città ha la sua regione unica. Questo è perfetto per essere una funzione perché non ci sono ambiguità.

Quando invece un elemento di A non è collegato a nulla, oppure è collegato a più elementi di B, allora non abbiamo più una funzione. È come se una città appartenesse a due regioni diverse - impossibile nella realtà!

💡 Ricorda: Una funzione è anche chiamata corrispondenza univoca proprio perché ogni elemento di partenza ha una destinazione unica e ben definita.

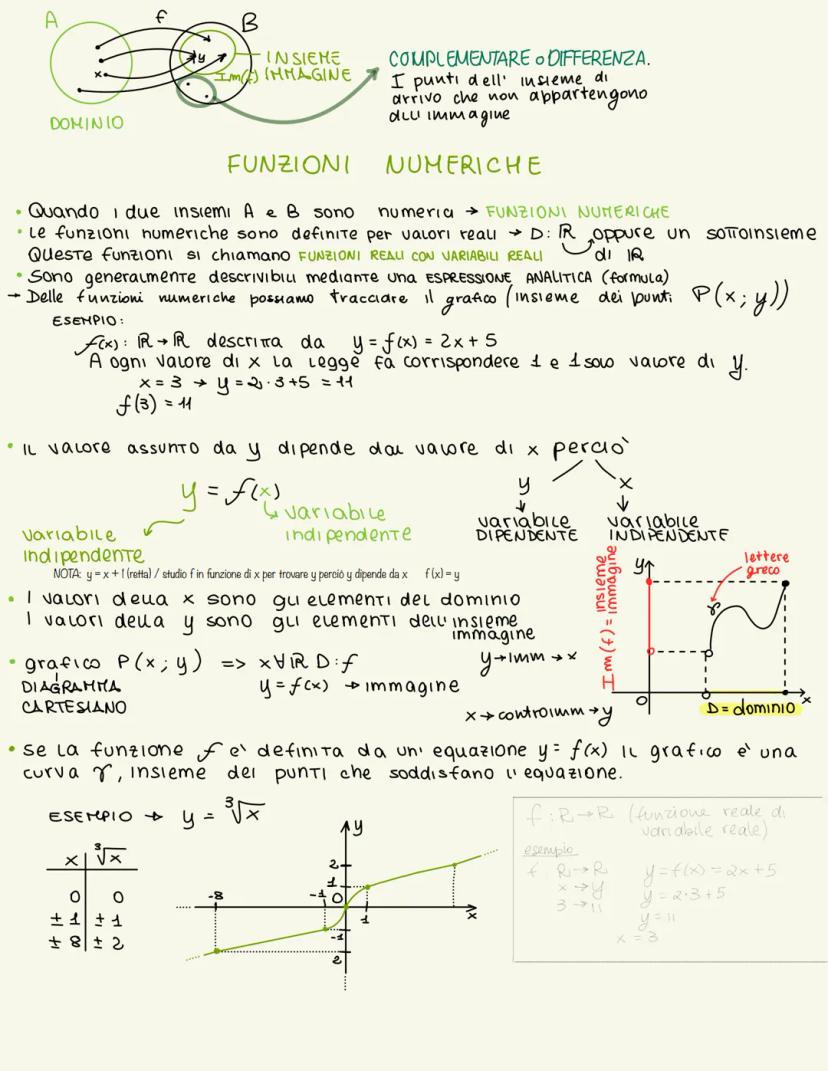
Per scrivere una funzione usiamo la notazione f: A → B (si legge "f è una funzione da A a B"). Quando un elemento x di A corrisponde a y di B, scriviamo y = f$x$ o f: x ↦ y.

Nel linguaggio delle funzioni, y è l'immagine di x e x è la controimmagine di y. L'insieme A si chiama dominio, l'insieme B si chiama codominio, mentre le immagini formano l'insieme immagine Im$f$.