Matematica

Limiti di Funzione e Asintoti

limite

Matematica4024 visualizzazioni·Aggiornato 17 lug 2026·7 pagine

Ripasso di Matematica Facile e Veloce

Lavinia Fortunato@lavfortunato

Aggiungi alle fonti Google

Qui trovi una guida completa su esponenziali, logaritmi, calcolo combinatorio,...

1 / 7

of 7

$# esponenziali • potenze con esponente intero o razionale esponente intero: $a^x se -> x > 0$; $\forall a$ ES. $(-\sqrt{2})^3 = -2\sqrt{2}$$

Funzioni Esponenziali

Le funzioni esponenziali sono quelle del tipo y = aˣ, dove la base "a" è un numero positivo diverso da 1. Sono ovunque nella vita reale: dalla crescita della popolazione ai calcoli finanziari!

La cosa più importante da ricordare è la distinzione tra i due casi principali. Se a > 1, la funzione è crescente $come y = 2ˣ$ , mentre se 0 < a < 1, è decrescente $come y = (1/2)ˣ$ . In entrambi i casi il dominio è sempre ℝ e il grafico passa sempre per il punto (0,1).

Per risolvere le equazioni esponenziali, cerca sempre di portare tutto alla stessa base. Se hai aᶠ⁽ˣ⁾ = aᵍ⁽ˣ⁾, allora f $x$ = g $x$ . Nelle disequazioni, ricorda che se la base è maggiore di 1 mantieni il verso, se è tra 0 e 1 lo cambi.

Trucco importante: Le funzioni esponenziali sono sempre positive e non toccano mai l'asse x!

of 7

$# esponenziali • potenze con esponente intero o razionale esponente intero: $a^x se -> x > 0$; $\forall a$ ES. $(-\sqrt{2})^3 = -2\sqrt{2}$$

Logaritmi e Calcolo Combinatorio

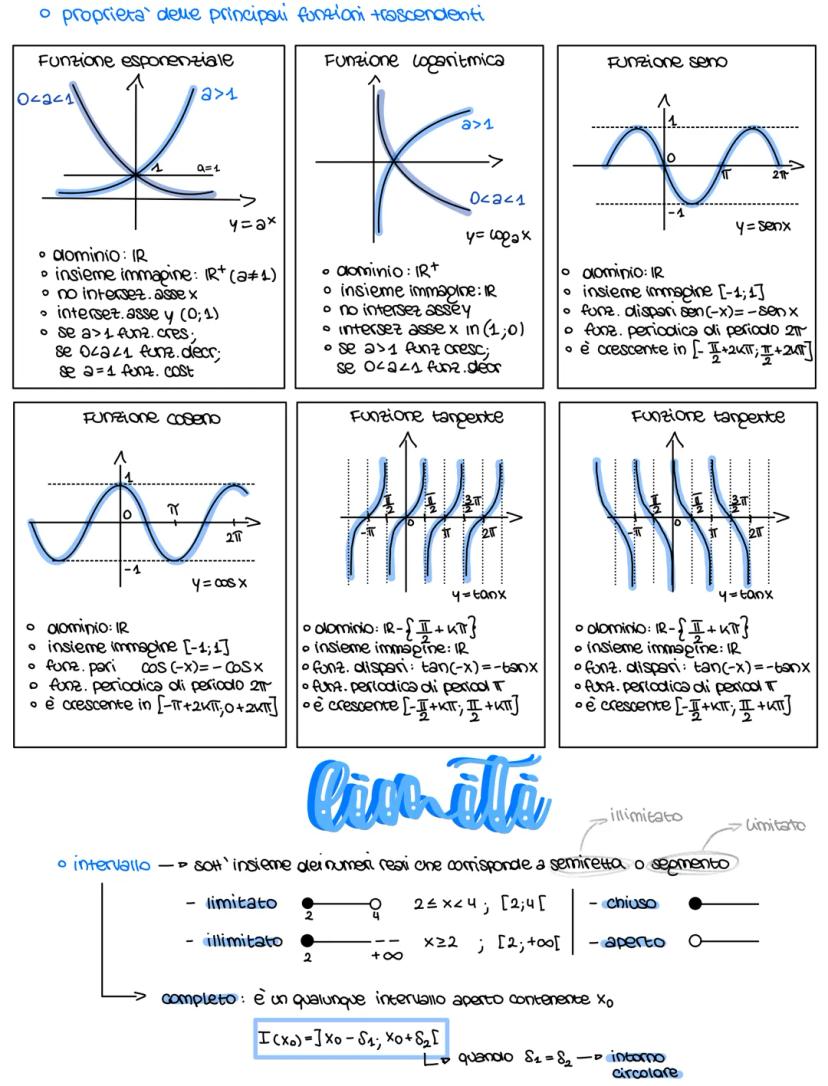
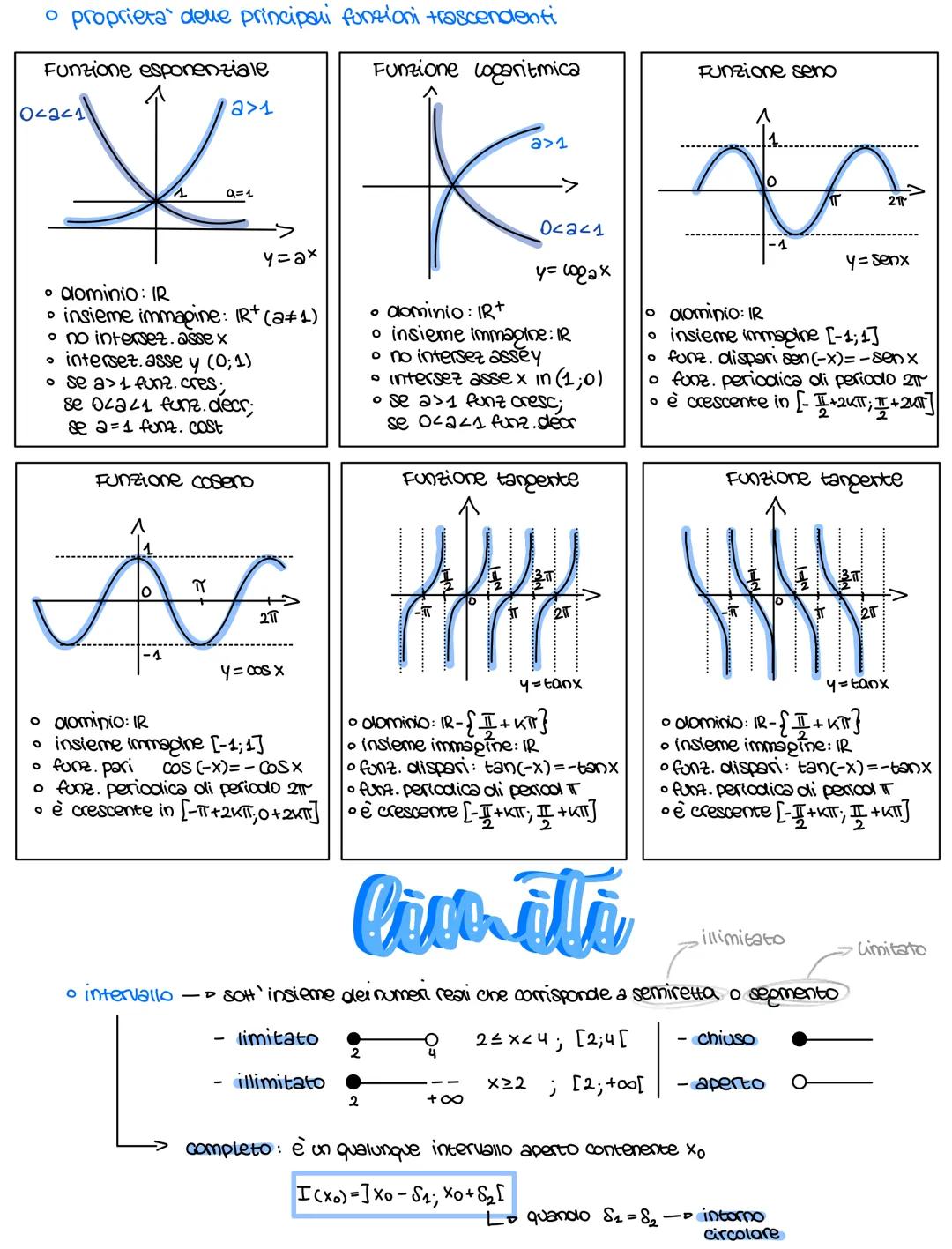
Il logaritmo è semplicemente l'operazione inversa dell'esponenziale. Se aˣ = b, allora x = log_a $b$ . È come chiedersi: "a che potenza devo elevare la base per ottenere questo numero?"

Le proprietà dei logaritmi sono fondamentali: log(AB) = log A + log B per i prodotti, log(A/B) = log A - log B per i quozienti, e log(Aⁿ) = n·log A per le potenze. Per cambiare base, usa la formula: log_c $b$ = log_a $b$ /log_a $c$ .

Nel calcolo combinatorio distingui bene tra disposizioni, permutazioni e combinazioni. Le disposizioni considerano l'ordine $D_{n,k} = n!/(n-k)!$ , le combinazioni no $C_{n,k} = n!/(k!(n-k)!)$ . Le permutazioni sono disposizioni di tutti gli elementi $P_n = n!$ .

Attenzione: Nelle funzioni logaritmiche il dominio è sempre ℝ⁺ (solo numeri positivi)!

of 7

$# esponenziali • potenze con esponente intero o razionale esponente intero: $a^x se -> x > 0$; $\forall a$ ES. $(-\sqrt{2})^3 = -2\sqrt{2}$$

Probabilità

La probabilità è il rapporto tra casi favorevoli e casi possibili: P(E) = f/n. Sembra banale, ma è la base di tutto il resto!

Per la somma logica di eventi, distingui tra eventi compatibili e incompatibili. Se sono incompatibili (uno esclude l'altro): P(E₁∪E₂) = P(E₁) + P(E₂). Se sono compatibili: P(E₁∪E₂) = P(E₁) + P(E₂) - P(E₁∩E₂).

Per il prodotto logico, se gli eventi sono indipendenti: P(E₁∩E₂) = P(E₁)·P(E₂). Se sono dipendenti, usi la probabilità condizionata: P(E₁∩E₂) = P(E₁)·P $E₂/E₁$ .

Ricorda: La probabilità dell'evento contrario è sempre P(Ē) = 1 - P(E)!

of 7

$# esponenziali • potenze con esponente intero o razionale esponente intero: $a^x se -> x > 0$; $\forall a$ ES. $(-\sqrt{2})^3 = -2\sqrt{2}$$

Funzioni: Definizioni e Trasformazioni

Una funzione associa ad ogni elemento del dominio uno e un solo elemento del codominio. Il dominio naturale è l'insieme più ampio dove la funzione ha senso matematico.

Le trasformazioni geometriche ti permettono di ottenere nuove funzioni da quelle base. Le traslazioni spostano il grafico: y = f $x-a$ sposta a destra, y = f $x$ + b sposta in alto. Le simmetrie riflettono: y = -f $x$ rispetto all'asse x, y = f $-x$ rispetto all'asse y.

Una funzione può essere iniettiva (ogni y ha al massimo una x), suriettiva (ogni y ha almeno una x), o biettiva (entrambe le cose). Le funzioni pari hanno f $x$ = f $-x$ , quelle dispari f $-x$ = -f $x$ .

Consiglio: Per capire le trasformazioni, parti sempre dalla funzione base e applica una trasformazione alla volta!

of 7

$# esponenziali • potenze con esponente intero o razionale esponente intero: $a^x se -> x > 0$; $\forall a$ ES. $(-\sqrt{2})^3 = -2\sqrt{2}$$

Funzioni Trascendenti e Intorni

Le funzioni trascendenti principali sono esponenziale, logaritmica e trigonometriche. L'esponenziale y = aˣ ha dominio ℝ e codominio ℝ⁺, è crescente se a>1. La logaritmica y = log_a $x$ è l'inversa, con dominio ℝ⁺ e codominio ℝ.

Le funzioni trigonometriche hanno caratteristiche specifiche. Seno e coseno hanno dominio ℝ, codominio $-1,1$ e periodo 2π. La tangente ha dominio ℝ - {π/2 + kπ}, codominio ℝ e periodo π.

Un intorno di un punto x₀ è un intervallo aperto che lo contiene: I(x₀) = ]x₀-δ; x₀+δ[. I punti di accumulazione hanno infiniti punti dell'insieme in ogni loro intorno, mentre i punti isolati hanno almeno un intorno che non contiene altri punti dell'insieme.

Nota bene: Le funzioni trigonometriche sono periodiche - ricordati sempre del periodo nelle equazioni!

of 7

$# esponenziali • potenze con esponente intero o razionale esponente intero: $a^x se -> x > 0$; $\forall a$ ES. $(-\sqrt{2})^3 = -2\sqrt{2}$$

Limiti: Definizioni e Calcolo

Il limite descrive il comportamento di una funzione quando x si avvicina a un valore. Se lim_{x→x₀} f $x$ = L, significa che f $x$ si avvicina arbitrariamente a L quando x si avvicina a x₀.

Una funzione è continua in x₀ se lim_{x→x₀} f $x$ = f(x₀). Gli asintoti verticali si hanno quando il limite è infinito $x = c$ , quelli orizzontali quando x tende a infinito $y = q$ .

Per il calcolo dei limiti, usa le proprietà: limite della somma = somma dei limiti, limite del prodotto = prodotto dei limiti, limite del quoziente = quoziente dei limiti (se il denominatore non è zero).

Attenzione: Le forme indeterminate $0/0, ∞/∞, +∞-∞, 0·∞$ richiedono tecniche speciali come razionalizzazione o raccoglimento!

of 7

$# esponenziali • potenze con esponente intero o razionale esponente intero: $a^x se -> x > 0$; $\forall a$ ES. $(-\sqrt{2})^3 = -2\sqrt{2}$$

Tecniche per le Forme Indeterminate

Le forme indeterminate sono situazioni dove le regole standard dei limiti non funzionano direttamente. Le principali sono: 0/0, ∞/∞, +∞-∞, 0·∞.

Per ∞/∞ con polinomi, raccogli la potenza più alta dal numeratore e denominatore. Il limite dipenderà dai coefficienti e dai gradi: se hanno stesso grado, il limite è il rapporto dei coefficienti principali.

Per 0/0, spesso devi scomporre e semplificare. Nelle irrazionalità, usa la razionalizzazione moltiplicando per il coniugato. Per le funzioni trigonometriche, sfrutta i limiti notevoli come lim_{x→0} (sin x)/x = 1.

Strategia vincente: Davanti a una forma indeterminata, prima prova il raccoglimento, poi la scomposizione, infine tecniche specifiche come la razionalizzazione!

Pensavamo che non l'avreste mai chiesto....

Il nostro assistente AI è costruito specificamente per le esigenze degli studenti. Sulla base dei milioni di contenuti presenti sulla piattaforma, possiamo fornire agli studenti risposte davvero significative e pertinenti. Ma non si tratta solo di risposte, l'assistente è in grado di guidare gli studenti attraverso le loro sfide quotidiane di studio, con piani di studio personalizzati, quiz o contenuti nella chat e una personalizzazione al 100% basata sulle competenze e sugli sviluppi degli studenti.

È possibile scaricare l'applicazione dal Google Play Store e dall'Apple App Store.

Sì, hai accesso completamente gratuito a tutti i contenuti nell'app e puoi chattare o seguire i Creatori in qualsiasi momento. Sbloccherai nuove funzioni crescendo il tuo numero di follower. Inoltre, offriamo Knowunity Premium, che consente di studiare senza alcun limite!!

Funzioni Esponenziali

Logaritmi e Calcolo Combinatorio

Probabilità

Funzioni: Definizioni e Trasformazioni

Funzioni Trascendenti e Intorni

Limiti: Definizioni e Calcolo

Tecniche per le Forme Indeterminate

Pensavamo che non l'avreste mai chiesto....

Che cos'è l'assistente AI di Knowunity?

Dove posso scaricare l'applicazione Knowunity?

Knowunity è davvero gratuita?

Contenuti simili

Appunti Teoria Matematica

I LIMITI

Topologia e funzioni

Limiti di Funzione

i limiti

Calcolo limiti e Limiti notevoli

Contenuti più popolari: limite

LIMITI - APPUNTI COMPLETI CON TEOREMI

Limiti

Limiti

Analisi matematica I

ANALISI MATEMATICA (TEORIA)

Limiti, teoremi, continuità e discontinuità

Limiti e limiti notevoli

TEOREMI DEI LIMITI

Limiti e verifica del limite

Contenuti più popolari di Matematica

Equazioni

i criteri di divisibilità

Formulario di mate

Matematica per la maturità

Fondamenti del Teorema di Pitagora

Formulario di matematica maturità 2024

Disequazioni di secondo grado

Piano cartesiano e retta

ecco un breve test per verificare le tue conoscenze sul teorema di Pitagora

Contenuti più popolari

Teoria patente b

Riassunto patente B

Aristotele

Teoria patente di guida B: Segnali stradali

I promessi sposi

Gabriele D'Annunzio e l'Estetismo

PATENTE

appunti patente

Sintesi finale di Analisi logica

Recensioni dei nostri utenti. Ci adorano - e anche tu, vedrai .

Iscriviti per mostrare il contenuto. È gratis!

Funzioni Esponenziali

Iscriviti per mostrare il contenuto. È gratis!

Logaritmi e Calcolo Combinatorio

Iscriviti per mostrare il contenuto. È gratis!

Probabilità

Iscriviti per mostrare il contenuto. È gratis!

Funzioni: Definizioni e Trasformazioni

Iscriviti per mostrare il contenuto. È gratis!

Funzioni Trascendenti e Intorni

Iscriviti per mostrare il contenuto. È gratis!

Limiti: Definizioni e Calcolo

Iscriviti per mostrare il contenuto. È gratis!

Tecniche per le Forme Indeterminate

Pensavamo che non l'avreste mai chiesto....

Che cos'è l'assistente AI di Knowunity?

Dove posso scaricare l'applicazione Knowunity?

Knowunity è davvero gratuita?

Contenuti simili

Appunti Teoria Matematica

I LIMITI

Topologia e funzioni

Limiti di Funzione

i limiti

Calcolo limiti e Limiti notevoli

Contenuti più popolari: limite

LIMITI - APPUNTI COMPLETI CON TEOREMI

Limiti

Limiti

Analisi matematica I

ANALISI MATEMATICA (TEORIA)