Matematica

Funzioni e Identità Trigonometriche

funzioni trigonometriche

Matematica6763Aggiornato 10 set 202610 pagine

Introduzione alla Goniometria e Trigonometria - Appunti Utili

Segnala

Monika Danese@monikadanese

Aggiungi alle fonti Google

La goniometria è lo studio delle funzioni trigonometriche e degli angoli - una parte fondamentale della matematica che ti servirà sia per gli esami che per molte applicazioni pratiche. Imparerai a convertire tra diverse unità di misura degli angoli, a usare le funzioni seno, coseno e tangente, e a risolvere equazioni e triangoli.

Iscriviti per mostrare il contenuto.
È gratis!

Accesso a tutti i documenti
Migliora i tuoi voti
Unisciti a milioni di studenti

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Misura degli Angoli e Funzioni Goniometriche Base

Gli angoli si possono misurare in gradi sessagesimali (come 48°17'26'') o sessadecimali (come 48,2905°). Per convertire da sessagesimali a sessadecimali, dividi i minuti per 60 e i secondi per 3600, poi somma tutto.

Un altro sistema importante sono i radianti, dove l'angolo è il rapporto tra l'arco e il raggio: θ = AB/r. La formula di conversione è: grad/180° = rad/π.

Le funzioni goniometriche fondamentali sono tre. Il seno è il rapporto tra cateto opposto e ipotenusa, il coseno tra cateto adiacente e ipotenusa, la tangente tra cateto opposto e cateto adiacente.

Ricorda sempre: cos²θ + sin²θ = 1, questa è l'identità fondamentale della goniometria!

Tutte e tre hanno periodo 2π (tranne la tangente che ha periodo π) e dominio nei reali, ma immagini diverse: seno e coseno vanno da -1 a 1, mentre la tangente copre tutti i reali.

Iscriviti per mostrare il contenuto.
È gratis!

Accesso a tutti i documenti
Migliora i tuoi voti
Unisciti a milioni di studenti

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Funzioni Goniometriche Inverse e Trasformazioni

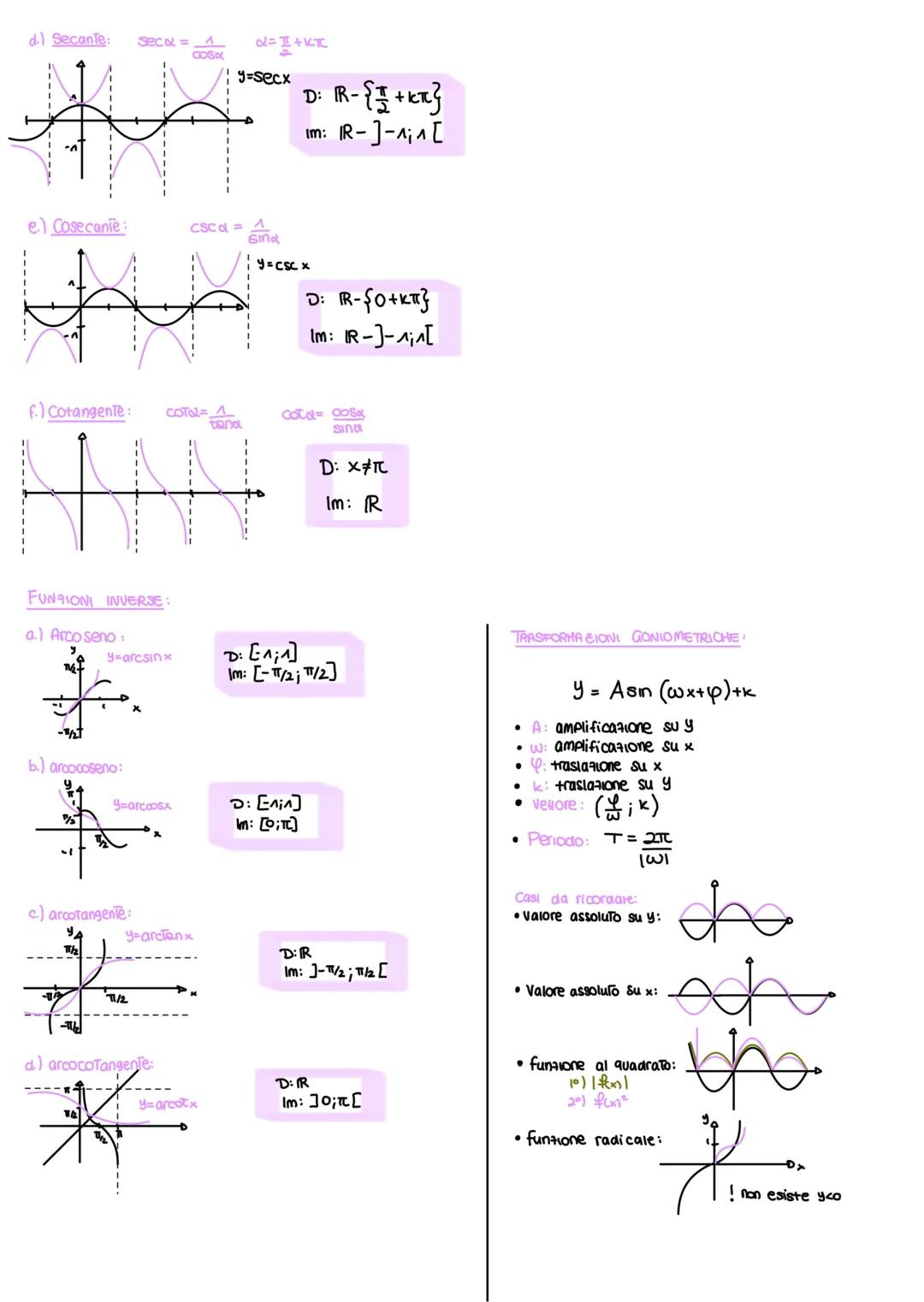
Le funzioni reciproche completano il quadro: secante $1/cos x$ , cosecante $1/sin x$ e cotangente $1/tan x$ . Attenzione ai domini - dove le funzioni originali si annullano, quelle reciproche non esistono.

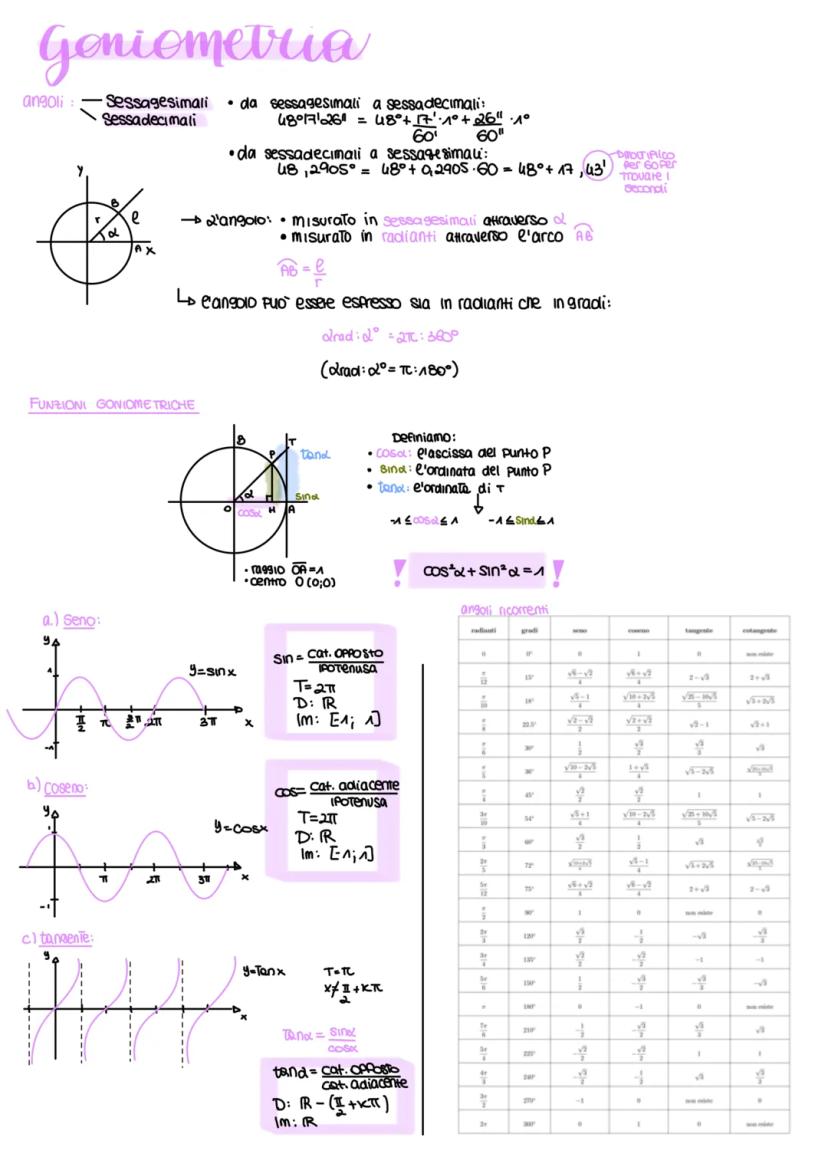
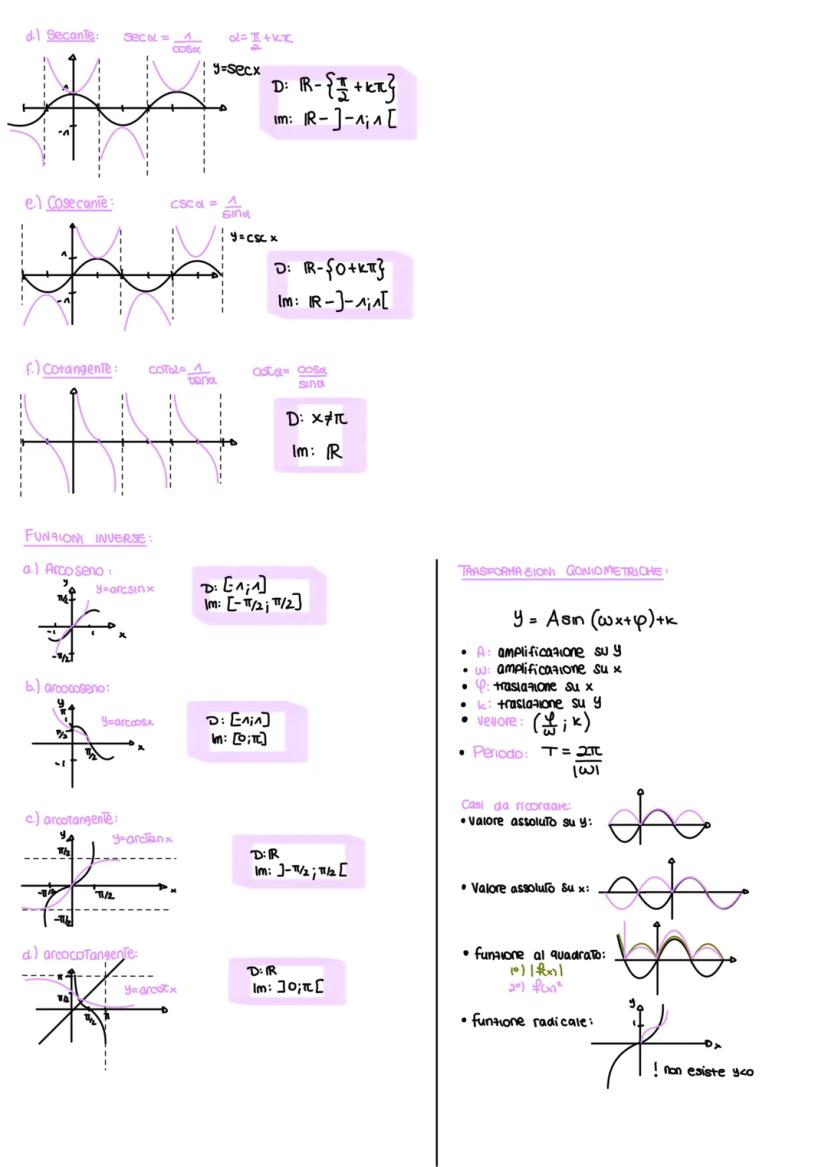
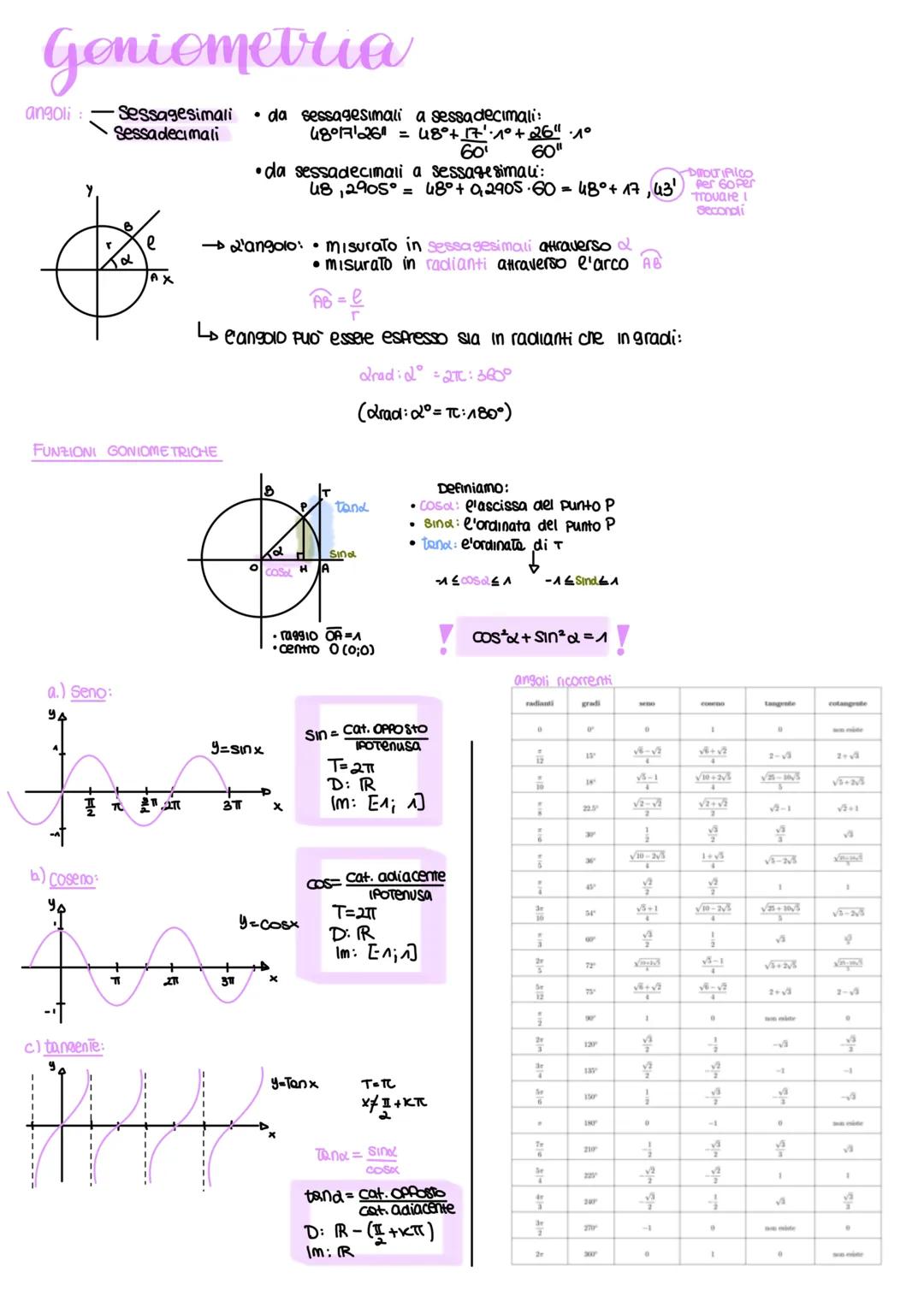
Le funzioni inverse ti permettono di "tornare indietro" dagli angoli. L'arcoseno ha dominio $-1,1$ e immagine $-π/2, π/2$ , l'arcocoseno stesso dominio ma immagine [0, π], mentre l'arcotangente ha dominio tutti i reali e immagine ]-π/2, π/2[.

Per le trasformazioni usa la forma y = A sin $wx + φ$ + k. A modifica l'ampiezza verticale, w quella orizzontale (il periodo diventa T = 2π/|w|), φ sposta orizzontalmente e k verticalmente.

Trucco utile: Quando vedi il valore assoluto di una funzione, rifletti la parte negativa sopra l'asse x!

I casi speciali includono funzioni al quadrato (sempre positive) e sotto radice (esistono solo dove la funzione è positiva).

Iscriviti per mostrare il contenuto.
È gratis!

Accesso a tutti i documenti
Migliora i tuoi voti
Unisciti a milioni di studenti

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Formule Goniometriche Essenziali

Le formule di addizione sono cruciali per semplificare espressioni complesse. Per il seno: sin(α ± β) = sin α cos β ± cos α sin β. Per il coseno: cos(α ± β) = cos α cos β ∓ sin α sin β.

Le formule di duplicazione derivano da quelle di addizione ponendo β = α. Quindi sin 2α = 2 sin α cos α, mentre cos 2α ha tre forme equivalenti: cos²α - sin²α, 1 - 2sin²α, oppure 2cos²α - 1.

Le formule di bisezione ti aiutano a calcolare sin $α/2$ e cos $α/2$ usando ± √ $(1 ∓ cos α)/2$ . Il segno dipende dal quadrante in cui cade α/2.

Strategia vincente: Le formule parametriche con t = tan $α/2$ semplificano molti calcoli complessi!

Le formule di prostaferesi trasformano somme in prodotti (utili per le equazioni), mentre quelle di Werner fanno l'opposto. Sono particolarmente utili negli integrali e nelle semplificazioni.

Iscriviti per mostrare il contenuto.
È gratis!

Accesso a tutti i documenti
Migliora i tuoi voti
Unisciti a milioni di studenti

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Equazioni Goniometriche

Le equazioni elementari come sin x = 1/2 hanno soluzioni periodiche. Per sin x = 1/2, hai x = π/6 + 2kπ oppure x = 5π/6 + 2kπ, dove k è un intero qualsiasi.

Le equazioni riconducibili si risolvono con sostituzioni. Ad esempio, sin $x - π/6$ = 1 diventa un'equazione elementare sostituendo u = x - π/6.

Per le equazioni di secondo grado come 2sin²x + 3sin x + 1 = 0, poni sin x = t e risolvi l'equazione algebrica. Poi risolvi le equazioni elementari ottenute.

Attenzione: Nelle equazioni con tangente, controlla sempre che cos x ≠ 0!

Le equazioni lineari del tipo sin x + cos x = λ si risolvono con le formule parametriche o elevando al quadrato (attento alle soluzioni spurie!). Il metodo grafico può aiutarti a visualizzare le soluzioni.

Iscriviti per mostrare il contenuto.
È gratis!

Accesso a tutti i documenti
Migliora i tuoi voti
Unisciti a milioni di studenti

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Disequazioni Goniometriche

Le disequazioni elementari come sin x ≥ 1/2 si risolvono graficamente. Devi trovare gli intervalli dove la funzione soddisfa la condizione. Per sin x ≥ 1/2, la soluzione è π/6 + 2kπ ≤ x ≤ 5π/6 + 2kπ.

Le disequazioni riconducibili seguono lo stesso principio delle equazioni: fai la sostituzione, risolvi, poi torna alla variabile originale.

Per le disequazioni di secondo grado, risolvi prima l'equazione associata per trovare gli zeri, poi studia il segno con una tabella. Questo ti dice dove la parabola è positiva o negativa.

Metodo infallibile: Disegna sempre il grafico della funzione - ti aiuta a vedere subito gli intervalli soluzione!

Le disequazioni fratte richiedono lo studio del segno di numeratore e denominatore separatamente. Ricorda: il denominatore non può mai essere zero, quindi escludi sempre questi valori.

Iscriviti per mostrare il contenuto.
È gratis!

Accesso a tutti i documenti
Migliora i tuoi voti
Unisciti a milioni di studenti

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Triangoli Rettangoli e Trigonometria

La trigonometria studia le relazioni tra lati e angoli nei triangoli. In un triangolo rettangolo, le definizioni delle funzioni goniometriche diventano concrete: sin α = cateto opposto/ipotenusa.

Il primo teorema dice che ogni cateto è uguale all'ipotenusa moltiplicata per il seno dell'angolo opposto (o per il coseno dell'angolo adiacente). Quindi a = c sin α e b = c cos α.

Il secondo teorema collega i cateti tra loro: ogni cateto è uguale all'altro cateto moltiplicato per la tangente dell'angolo opposto. Quindi a = b tan α.

Ricorda: In un triangolo rettangolo, i due angoli acuti sono sempre complementari $α + β = 90°$ !

Queste relazioni sono fondamentali per risolvere i triangoli rettangoli - cioè trovare tutti i lati e angoli quando ne conosci alcuni. Le combinazioni possibili sono: due cateti, cateto e ipotenusa, cateto e angolo, ipotenusa e angolo.

Iscriviti per mostrare il contenuto.
È gratis!

Accesso a tutti i documenti
Migliora i tuoi voti
Unisciti a milioni di studenti

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Risoluzione Completa dei Triangoli Rettangoli

Quando conosci due cateti a e b, usi Pitagora per l'ipotenusa: c = √ $a² + b²$ . Per gli angoli: α = arctan(a/b) e β = 90° - α.

Con cateto e ipotenusa (a e c), trovi l'angolo con α = arcsin(a/c), poi β = 90° - α. L'altro cateto lo calcoli con Pitagora: b = √ $c² - a²$ .

Con cateto e angolo acuto (a e α), hai β = 90° - α direttamente. Il secondo cateto è b = a tan β, l'ipotenusa c = √ $a² + b²$ .

Verifica sempre: Controlla che α + β = 90° e che c² = a² + b² - è un ottimo modo per evitare errori!

Con ipotenusa e angolo (c e α), calcoli i cateti direttamente: a = c sin α e b = c sin β $dove β = 90° - α$ . Questo caso è spesso il più semplice da risolvere.

Iscriviti per mostrare il contenuto.
È gratis!

Accesso a tutti i documenti
Migliora i tuoi voti
Unisciti a milioni di studenti

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Teoremi Fondamentali per Triangoli Qualunque

Il teorema dell'area dice che l'area di qualsiasi triangolo è metà del prodotto di due lati per il seno dell'angolo compreso: Area = $1/2$ × lato₁ × lato₂ × sin(angolo compreso).

Il teorema della corda stabilisce che una corda è uguale al diametro moltiplicato per il seno di uno degli angoli alla circonferenza: AB = 2r sin α.

Da questo deriva la formula per il raggio della circonferenza circoscritta: r = a/(2 sin α) = b/(2 sin β) = c/(2 sin γ). Questo raggio è uguale per tutti e tre i lati.

Applicazione pratica: Questi teoremi sono essenziali per calcolare distanze e altezze in topografia e ingegneria!

La circonferenza circoscritta passa per tutti e tre i vertici del triangolo, e il suo centro è l'intersezione degli assi dei lati. Il raggio si calcola facilmente con una delle tre formule equivalenti.

Iscriviti per mostrare il contenuto.
È gratis!

Accesso a tutti i documenti
Migliora i tuoi voti
Unisciti a milioni di studenti

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Teoremi dei Seni e del Coseno

Il teorema dei seni è potentissimo: in qualsiasi triangolo, il rapporto tra un lato e il seno dell'angolo opposto è costante. Quindi a/sin α = b/sin β = c/sin γ = 2r.

Il teorema del coseno generalizza Pitagora per triangoli non rettangoli: a² = b² + c² - 2bc cos α. Quando α = 90°, cos α = 0 e ritrovi Pitagora!

Per triangoli con lato e due angoli noti, usi prima la somma degli angoli $α + β + γ = 180°$ per trovare il terzo angolo, poi applichi i seni per trovare gli altri lati.

Strategia chiave: Il teorema dei seni è perfetto quando hai angoli, quello del coseno quando hai principalmente lati!

Questi teoremi ti permettono di risolvere qualsiasi triangolo, purché tu abbia almeno tre elementi di cui almeno uno sia un lato. Sono la base per tutta la trigonometria applicata.

Iscriviti per mostrare il contenuto.
È gratis!

Accesso a tutti i documenti
Migliora i tuoi voti
Unisciti a milioni di studenti

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Risoluzione Avanzata di Triangoli Qualunque

Con due lati e angolo compreso (b, c, α), usi il coseno per trovare il terzo lato: a = √(b² + c² - 2bc cos α). Poi riapplichi il coseno per un secondo angolo.

Il caso due lati e angolo opposto (α, a, b) è più complesso. Usi i seni per trovare sin β = (b sin α)/a. Attenzione: se sin β ha due soluzioni, potresti avere due triangoli diversi!

Il caso ambiguo si verifica quando 0 < sin β < 1. Hai β₁ acuto e β₂ = 180° - β₁ ottuso. Devi verificare quale $i$ è geometricamente possibile considerando le dimensioni relative dei lati.

Controllo essenziale: Al lato maggiore è sempre opposto l'angolo maggiore - usa questa regola per eliminare soluzioni impossibili!

Dopo aver trovato tutti gli angoli, calcoli l'ultimo lato con i seni: c = (a sin γ)/sin α. Verifica sempre che tutti gli angoli siano positivi e minori di 180°.

Pensavamo che non l'avreste mai chiesto....

Il nostro assistente AI è costruito specificamente per le esigenze degli studenti. Sulla base dei milioni di contenuti presenti sulla piattaforma, possiamo fornire agli studenti risposte davvero significative e pertinenti. Ma non si tratta solo di risposte, l'assistente è in grado di guidare gli studenti attraverso le loro sfide quotidiane di studio, con piani di studio personalizzati, quiz o contenuti nella chat e una personalizzazione al 100% basata sulle competenze e sugli sviluppi degli studenti.

È possibile scaricare l'applicazione dal Google Play Store e dall'Apple App Store.

Sì, hai accesso completamente gratuito a tutti i contenuti nell'app e puoi chattare o seguire i Creatori in qualsiasi momento. Sbloccherai nuove funzioni crescendo il tuo numero di follower. Inoltre, offriamo Knowunity Premium, che consente di studiare senza alcun limite!!

Introduzione alla Goniometria e Trigonometria - Appunti Utili

Misura degli Angoli e Funzioni Goniometriche Base

Funzioni Goniometriche Inverse e Trasformazioni

Formule Goniometriche Essenziali

Equazioni Goniometriche

Disequazioni Goniometriche

Triangoli Rettangoli e Trigonometria

Risoluzione Completa dei Triangoli Rettangoli

Teoremi Fondamentali per Triangoli Qualunque

Teoremi dei Seni e del Coseno

Risoluzione Avanzata di Triangoli Qualunque

Pensavamo che non l'avreste mai chiesto....

Che cos'è l'assistente AI di Knowunity?

Dove posso scaricare l'applicazione Knowunity?

Knowunity è davvero gratuita?

Contenuti simili

Angoli e Funzioni Goniometriche

funzioni di seno e coseno

Goniometria

GONIOMETRIA : SENO, COSENO, TANGENTE E COTANGENTE

Goniometria

seno, coseno e tangente di un’angolo

Contenuti più popolari: funzioni trigonometriche

Trigonometria

Goniometria - funzione seno e coseno

Goniometria

Trigonometria

Funzioni goniometriche

goniometria e trigonometria

Goniometria

Funzioni Goniometriche

Grafici di funzioni elementari

Contenuti più popolari: Matematica

Prima parte programma matematica test professioni sanitarie

Formulario mate TOLC PSI

Preparazione Matrmatica TOLC-E

Preparazione Tolc I

Seconda parte programma matematica test professioni sanitarie

Formulario di mate

Tolc - simulazione sezione di logica - ingegneria

Prodotti notevoli

I logaritmi e le equazioni e disequazioni logaritmiche

Contenuti più popolari

Riassunto patente B

Teoria patente b

appunti patente

Teoria patente di guida B: Segnali stradali

Patente B

Prima parte programma biologia test professioni sanitarie

Patente

Programma chimica test professioni sanitarie

🚗 Teoria Patente B Completa + Errori Frequenti Quiz 2026

Recensioni dei nostri utenti. Ci adorano - e anche tu, vedrai .