Analisi completa: ripasso ed esempi
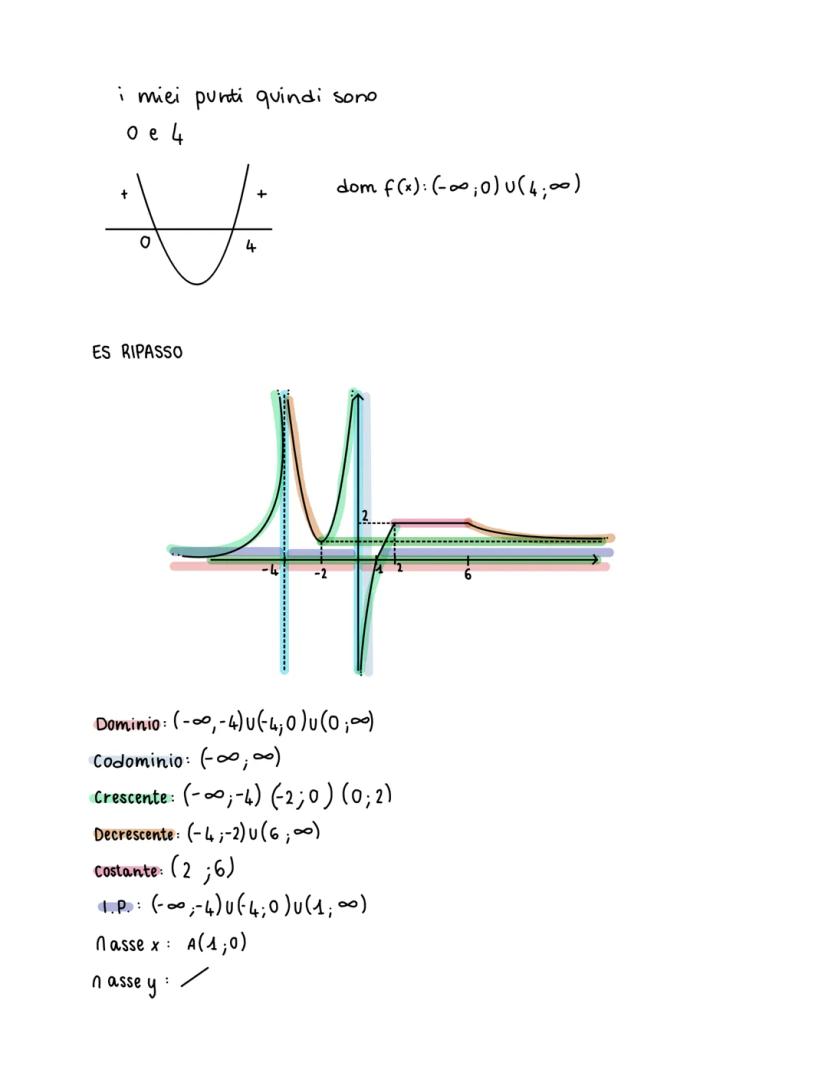
Quando risolvi esercizi di ripasso, segui sempre lo stesso schema: dominio, codominio, monotonia crescente/decrescente, insieme di positività, intersezioni, asintoti.
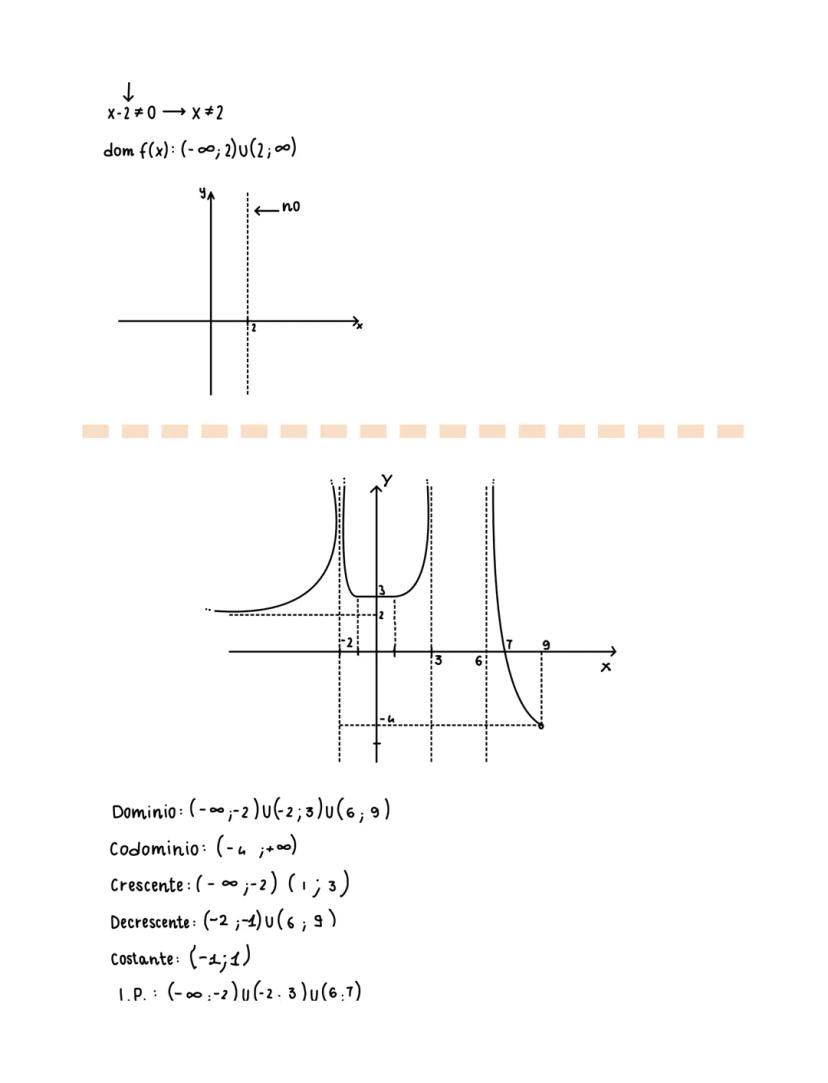
Per le funzioni razionali complesse, il codominio spesso è tutto ℝ, mentre il dominio esclude i punti che annullano il denominatore.
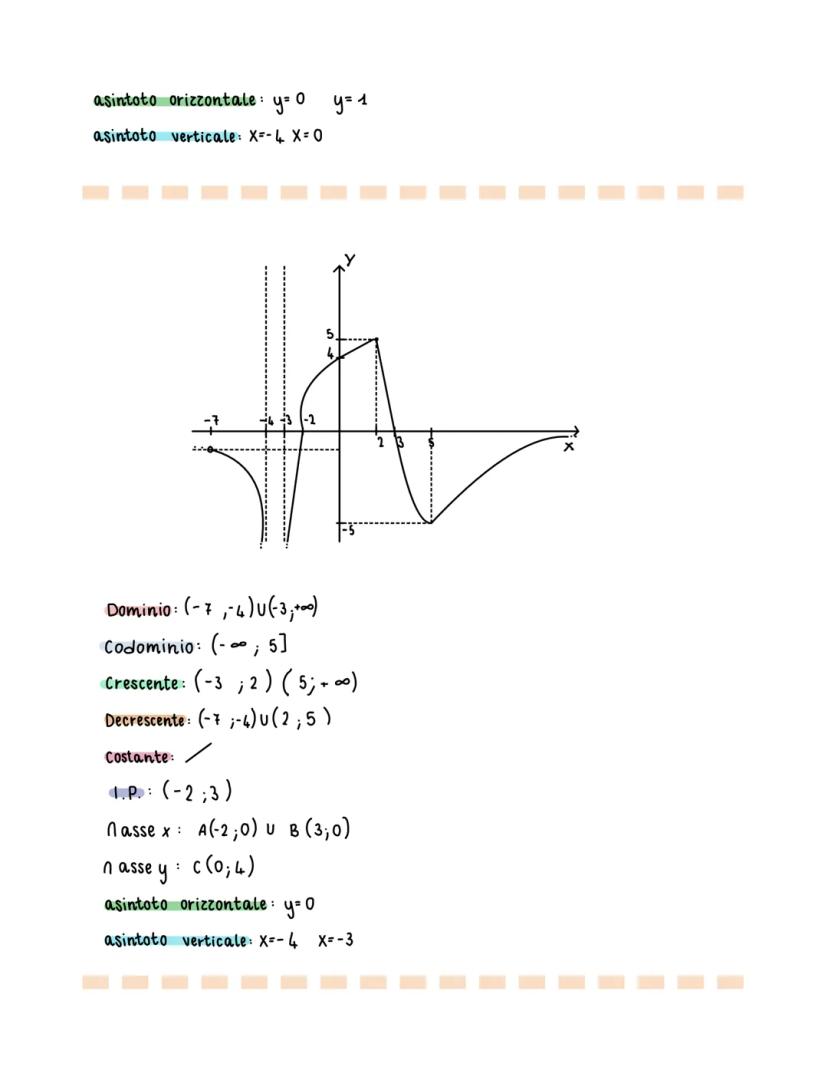
Gli asintoti orizzontali multipli possono esistere quando la funzione ha comportamenti diversi per x → +∞ e x → -∞.
Consiglio finale: Fai sempre un grafico approssimativo mentale per verificare che i tuoi calcoli abbiano senso dal punto di vista grafico.






![parentesi () pacentesi []
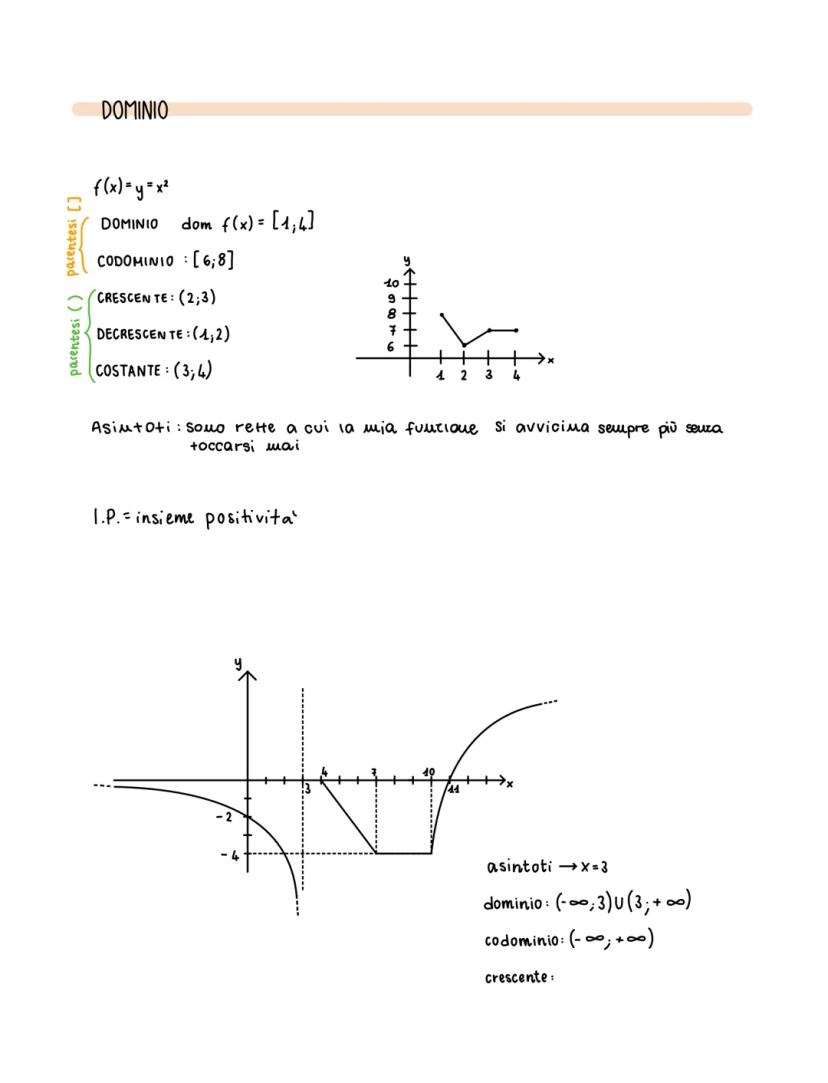
DOMINIO
$f(x) = y = x^2$
DOMINIO
dom $f(x) = [1,4]$
CODOMINIO: [6;8]
CRESCENTE: (2;3)
DECRESCENTE: (1,2)
C](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2FxUtvyLkMsbpDxnJLlaHs_image_page_1.webp&w=2048&q=75)
![parentesi () pacentesi []
DOMINIO
$f(x) = y = x^2$
DOMINIO
dom $f(x) = [1,4]$
CODOMINIO: [6;8]
CRESCENTE: (2;3)
DECRESCENTE: (1,2)
C](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2FxUtvyLkMsbpDxnJLlaHs_image_page_2.webp&w=2048&q=75)
![parentesi () pacentesi []
DOMINIO
$f(x) = y = x^2$
DOMINIO
dom $f(x) = [1,4]$
CODOMINIO: [6;8]
CRESCENTE: (2;3)
DECRESCENTE: (1,2)
C](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2FxUtvyLkMsbpDxnJLlaHs_image_page_3.webp&w=2048&q=75)
![parentesi () pacentesi []
DOMINIO
$f(x) = y = x^2$
DOMINIO
dom $f(x) = [1,4]$
CODOMINIO: [6;8]
CRESCENTE: (2;3)
DECRESCENTE: (1,2)
C](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2FxUtvyLkMsbpDxnJLlaHs_image_page_4.webp&w=2048&q=75)
![parentesi () pacentesi []
DOMINIO
$f(x) = y = x^2$
DOMINIO
dom $f(x) = [1,4]$
CODOMINIO: [6;8]
CRESCENTE: (2;3)
DECRESCENTE: (1,2)
C](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2FxUtvyLkMsbpDxnJLlaHs_image_page_5.webp&w=2048&q=75)
![parentesi () pacentesi []
DOMINIO
$f(x) = y = x^2$
DOMINIO
dom $f(x) = [1,4]$
CODOMINIO: [6;8]
CRESCENTE: (2;3)
DECRESCENTE: (1,2)
C](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2FxUtvyLkMsbpDxnJLlaHs_image_page_6.webp&w=2048&q=75)
![parentesi () pacentesi []
DOMINIO
$f(x) = y = x^2$
DOMINIO
dom $f(x) = [1,4]$
CODOMINIO: [6;8]
CRESCENTE: (2;3)
DECRESCENTE: (1,2)
C](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2FxUtvyLkMsbpDxnJLlaHs_image_page_7.webp&w=2048&q=75)
![parentesi () pacentesi []
DOMINIO
$f(x) = y = x^2$
DOMINIO
dom $f(x) = [1,4]$
CODOMINIO: [6;8]
CRESCENTE: (2;3)
DECRESCENTE: (1,2)
C](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2FxUtvyLkMsbpDxnJLlaHs_image_page_8.webp&w=2048&q=75)
![parentesi () pacentesi []
DOMINIO
$f(x) = y = x^2$
DOMINIO
dom $f(x) = [1,4]$
CODOMINIO: [6;8]
CRESCENTE: (2;3)
DECRESCENTE: (1,2)
C](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2FxUtvyLkMsbpDxnJLlaHs_image_page_9.webp&w=2048&q=75)
![parentesi () pacentesi []
DOMINIO
$f(x) = y = x^2$
DOMINIO
dom $f(x) = [1,4]$
CODOMINIO: [6;8]
CRESCENTE: (2;3)
DECRESCENTE: (1,2)
C](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2FxUtvyLkMsbpDxnJLlaHs_image_page_10.webp&w=2048&q=75)