Classificazione delle Funzioni e Studio del Dominio

Prima di tutto, devi saper classificare le funzioni per capire come approcciarle. Le funzioni si dividono in algebriche (con operazioni come addizione, moltiplicazione, radici) e trascendenti (esponenziali, logaritmiche, goniometriche).

Il primo passo dello studio è sempre trovare il dominio. Per le funzioni razionali intere come $y = x^4 - x^2$, il dominio è sempre $\mathbb{R}$. Per quelle fratte, devi escludere i valori che annullano il denominatore.

Le funzioni irrazionali con indice pari richiedono che l'argomento sia non negativo, mentre quelle con indice dispari sono definite ovunque. Per i logaritmi, ricorda che l'argomento deve essere sempre positivo.

Trucco importante: Per le funzioni goniometriche, seno e coseno sono sempre definiti, mentre la tangente ha problemi quando l'argomento vale $\frac{\pi}{2} + k\pi$.

Intersezioni, Simmetrie e Comportamento agli Estremi

Per trovare le intersezioni con gli assi, calcola $f(0)$ per l'asse y e risolvi $f(x) = 0$ per l'asse x. Questi punti ti daranno i primi riferimenti importanti per il grafico.

Le simmetrie ti semplificano molto il lavoro! Una funzione è pari se $f(-x) = f(x)$ (simmetrica rispetto all'asse y) e dispari se $f(-x) = -f(x)$ (simmetrica rispetto all'origine).

Il comportamento agli estremi rivela la presenza di asintoti. Gli asintoti verticali si hanno quando $\lim_{x \to x_0} f(x) = \pm \infty$, quelli orizzontali quando $\lim_{x \to \pm \infty} f(x) = l$.

Attenzione: Per gli asintoti obliqui, devi verificare che il limite per $x \to \pm \infty$ sia infinito, poi calcolare $m = \lim \frac{f(x)}{x}$ e $q = \lim [f(x) - mx]$.

Derivate e Studio Completo di un Esempio

La derivata prima $f'(x)$ ti dice dove la funzione cresce o decresce. Quando $f'(x) > 0$ la funzione è crescente, quando $f'(x) < 0$ è decrescente. I punti dove $f'(x) = 0$ possono essere massimi, minimi o flessi a tangente orizzontale.

La derivata seconda $f''(x)$ determina la concavità: se $f''(x) > 0$ la funzione volge la concavità verso l'alto, se $f''(x) < 0$ verso il basso. I punti di flesso si trovano risolvendo $f''(x) = 0$.

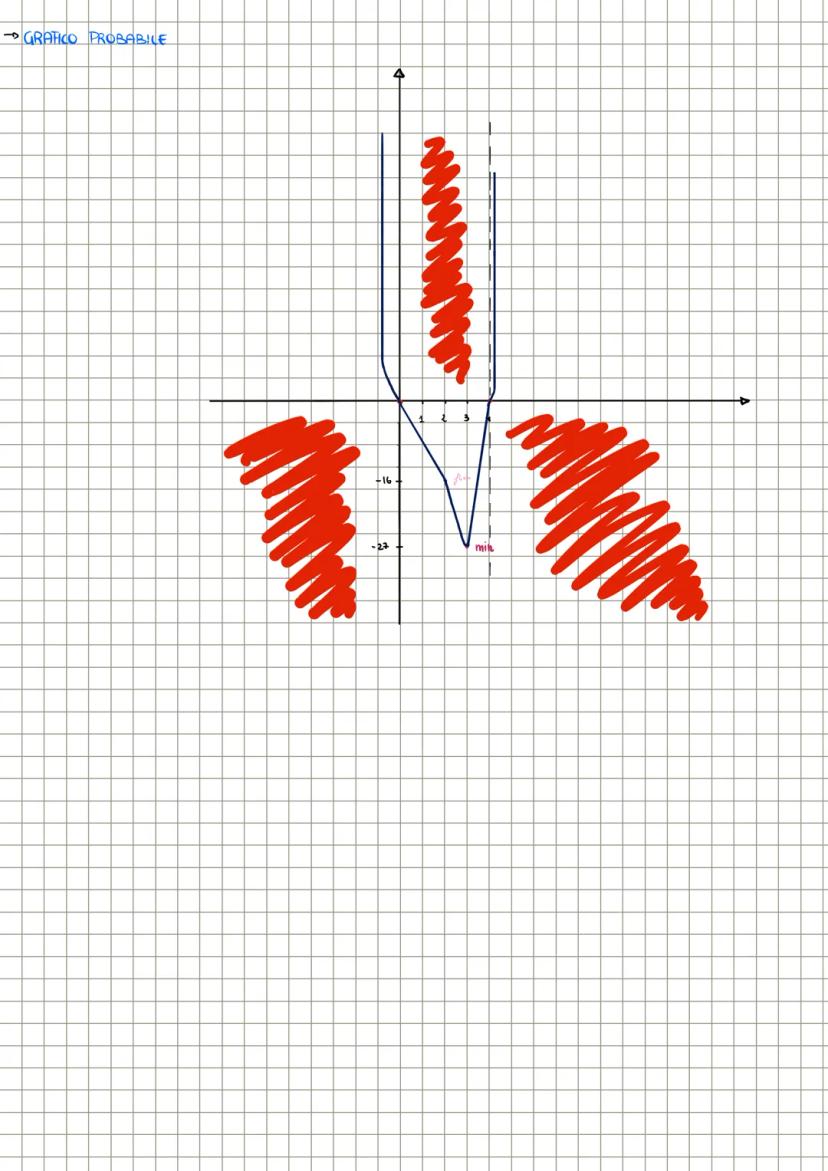
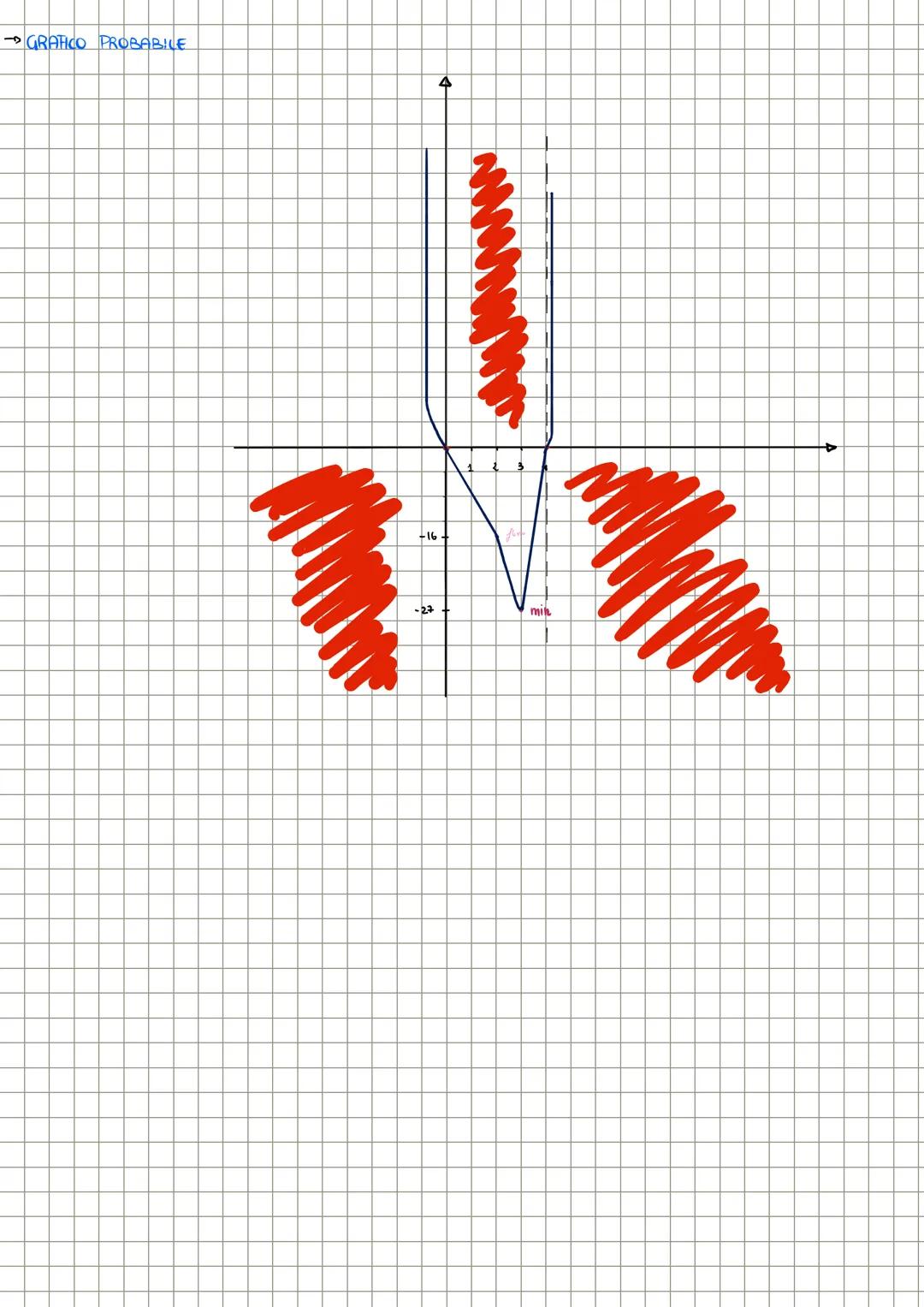
Nell'esempio $y = x^2 - 4x^3$, vediamo che il dominio è $\mathbb{R}$, le intersezioni sono in $(0,0)$ e $(4,0)$, non ha simmetrie particolari. La derivata prima $y' = 4x^3 - 12x^2$ ci mostra che la funzione è crescente per $x > 3$.

Consiglio pratico: Una volta calcolate entrambe le derivate, fai sempre una tabella dei segni per visualizzare meglio crescita, decrescita e concavità.

Costruzione del Grafico Finale

Ora che hai raccolto tutte le informazioni (dominio, intersezioni, limiti, derivate), è il momento di tracciare il grafico. Inizia segnando i punti di intersezione con gli assi e i punti critici trovati con le derivate.

Usa le informazioni sulla crescita e decrescita per capire come collegare i punti, rispettando sempre la concavità indicata dalla derivata seconda. Non dimenticare di rappresentare correttamente gli asintoti come linee tratteggiate.

Il grafico finale deve essere coerente con tutti i calcoli precedenti: se hai trovato un massimo in un certo punto, assicurati che il grafico effettivamente "salga e poi scenda" in quel punto.