Matematica

Regole Fondamentali di Derivazione

Regole di Differenziazione

Matematica1484Aggiornato 30 set 20263 pagine

Studio Completo di Funzione: Guida per Studenti

Segnala

Domenico@mimmix

Aggiungi alle fonti Google

Lo studio di funzione può sembrare complicato, ma è solo una serie di passaggi logici che ti permettono di "smontare" una funzione per capire come si comporta. Imparerai a trovare il dominio, studiare limiti e asintoti, e usare le derivate per tracciare il grafico perfetto.

Iscriviti per mostrare il contenuto.
È gratis!

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Dominio e prime analisi

Trovare il dominio è il primo passo fondamentale: devi capire per quali valori di x la funzione "funziona" davvero. Per le funzioni razionali intere come y=2x+3, il dominio è sempre ℝ perché non ci sono problemi.

Le cose si complicano con le funzioni razionali fratte come y= $4x+2$ / $x+3$ . Qui devi escludere i valori che rendono zero il denominatore: x+3≠0, quindi x≠-3.

Per le funzioni irrazionali con radice quadrata, l'argomento deve essere ≥0. Se hai y=√ $4x+2$ , serve 4x+2≥0. Nelle funzioni esponenziali come y=2^ $x+3$ l'argomento deve essere >0, mentre nelle logaritmiche come y=log(2x) serve 2x>0.

Dopo il dominio, controlla le simmetrie: una funzione è pari se f $x$ =f $-x$ , dispari se -f $x$ =f $-x$ , altrimenti è asimmetrica.

Trucco: Per trovare rapidamente le intersezioni, poni x=0 per l'asse y e y=0 per l'asse x!

Iscriviti per mostrare il contenuto.
È gratis!

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Limiti e asintoti

I limiti ti dicono come si comporta la funzione quando x si avvicina a certi valori o va all'infinito. Sono essenziali per trovare gli asintoti, quelle rette che la funzione "tocca" ma non attraversa mai.

Se lim(x→x₀) f $x$ = ±∞, hai un asintoto verticale x=x₀. Se lim(x→±∞) f $x$ = k (numero), hai un asintoto orizzontale y=k.

Per l'asintoto obliquo y=mx+q, calcoli m = lim(x→±∞) f $x$ /x e poi q = lim(x→±∞) $f(x)-mx$ . Se m non esiste o è infinito, non c'è asintoto obliquo.

I prodotti notevoli sono i tuoi migliori amici per semplificare: differenza di quadrati $a²-b²$ , trinomio speciale $x²+bx+c$ , cubo di binomio. La regola di Ruffini ti salva quando devi scomporre polinomi di grado superiore al secondo.

Ricorda: Nelle frazioni, il grado maggiore "vince" sempre nel comportamento all'infinito!

Iscriviti per mostrare il contenuto.
È gratis!

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Derivate e studio della funzione

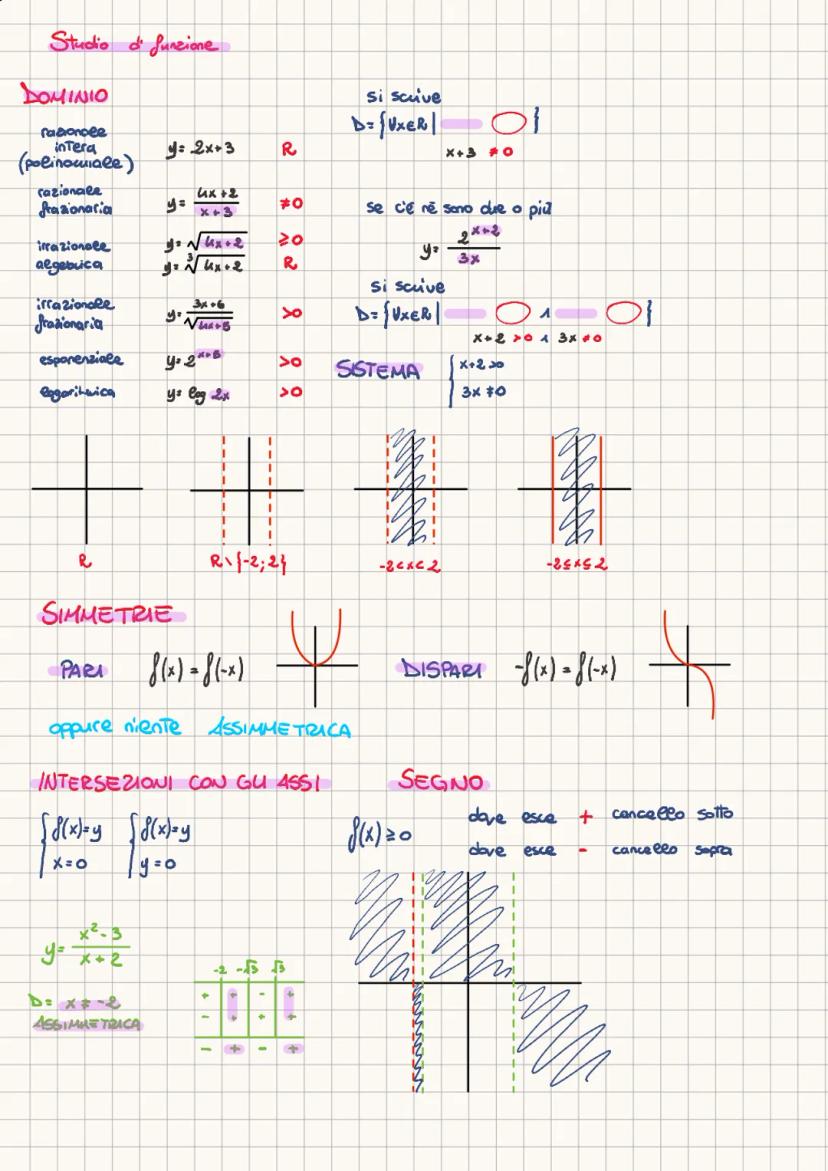
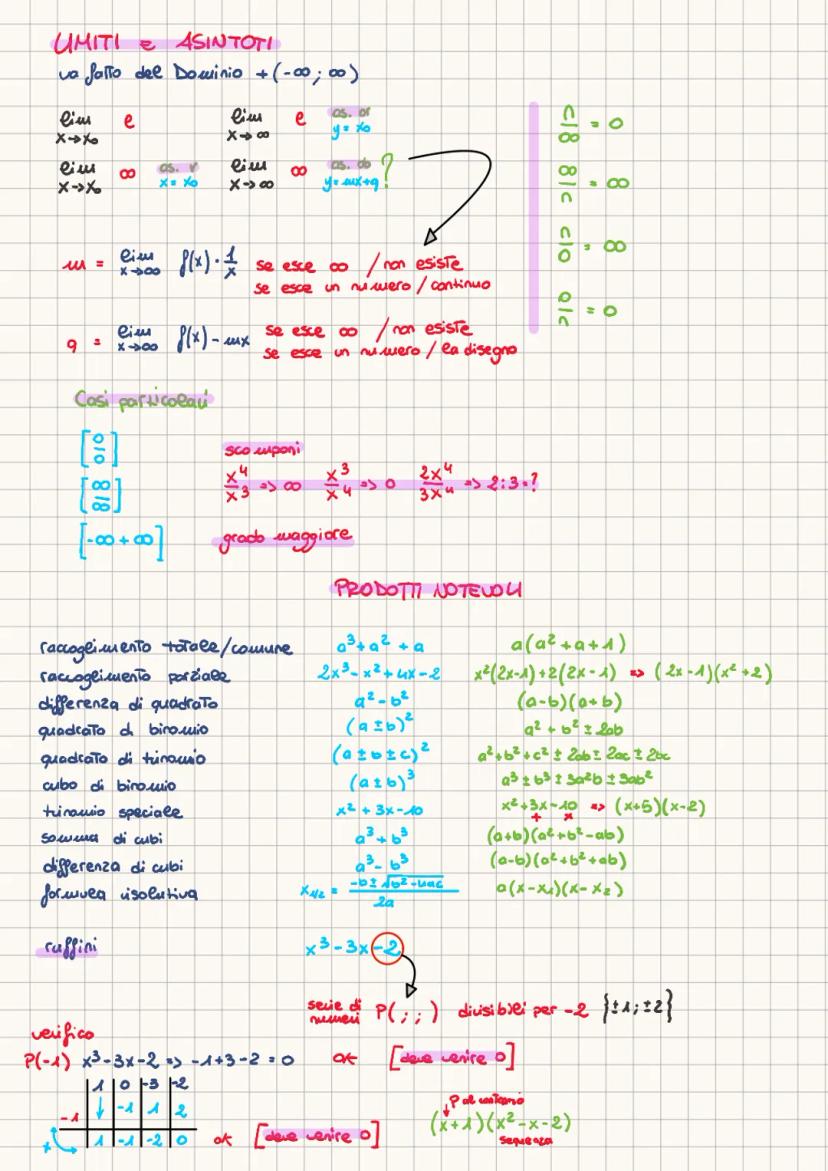
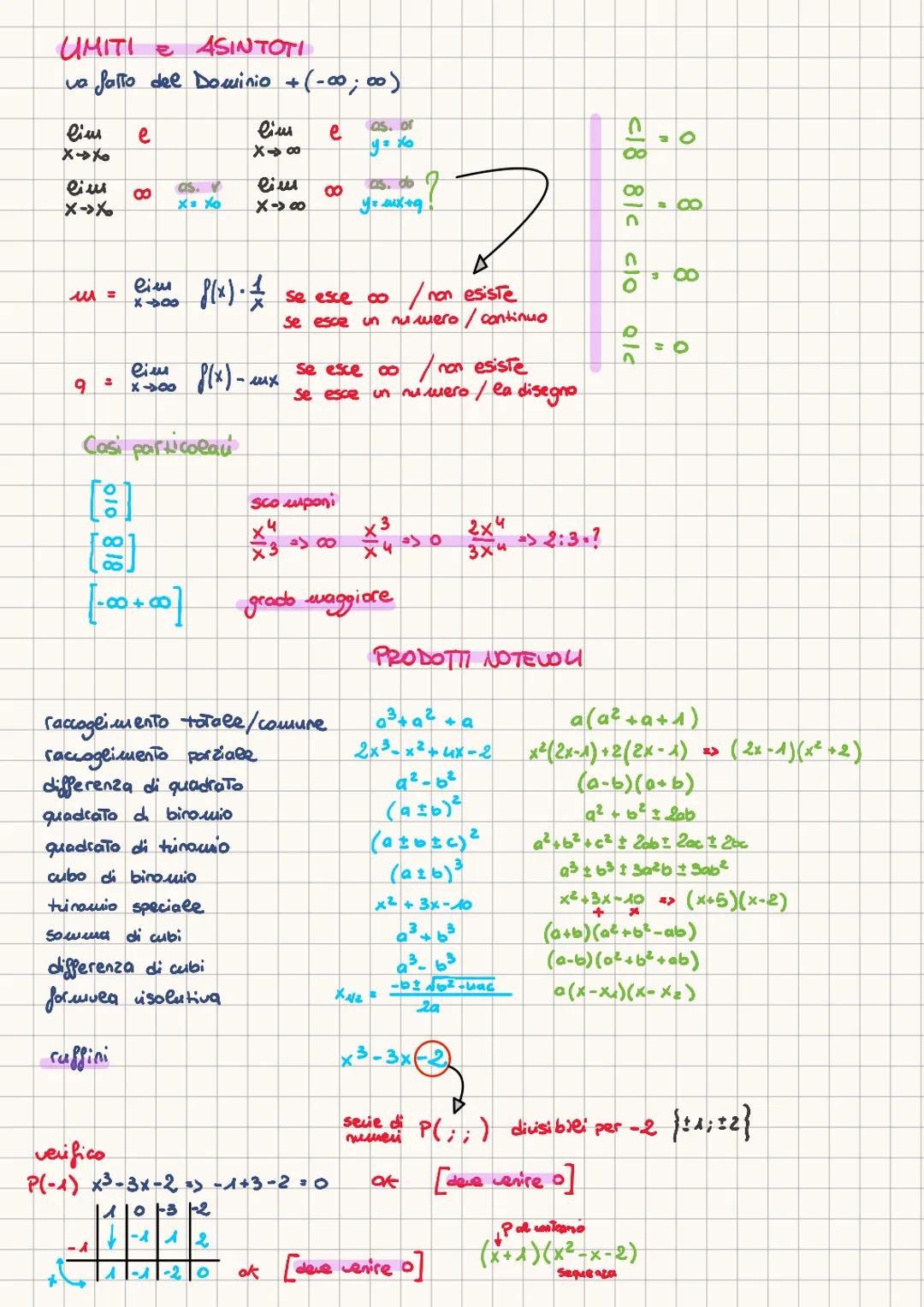
La derivata prima y' ti dice dove la funzione cresce (y'>0) o decresce (y'<0). Quando y'=0, hai dei punti critici: potrebbero essere massimi, minimi o punti di flesso.

La derivata seconda y'' rivela la concavità: se y''>0 la funzione è concava verso l'alto (sorriso), se y''<0 è concava verso il basso (smorfie). Quando y''=0, potresti avere un punto di flesso.

Le regole di derivazione sono fondamentali: derivata di x^n è nx^ $n-1$ , di e^x è e^x, di ln $x$ è 1/x. Per le funzioni composte usa la regola della catena, per i quozienti la formula $N'D-ND'$ /D².

Combinando derivata prima e seconda ottieni il grafico completo: crescenza/decrescenza, massimi/minimi, concavità e flessi. È come avere la mappa completa del comportamento della funzione.

Strategia vincente: Fai sempre una tabella con i segni di y' e y'' - ti renderà tutto più chiaro visivamente!

Pensavamo che non l'avreste mai chiesto....

Il nostro assistente AI è costruito specificamente per le esigenze degli studenti. Sulla base dei milioni di contenuti presenti sulla piattaforma, possiamo fornire agli studenti risposte davvero significative e pertinenti. Ma non si tratta solo di risposte, l'assistente è in grado di guidare gli studenti attraverso le loro sfide quotidiane di studio, con piani di studio personalizzati, quiz o contenuti nella chat e una personalizzazione al 100% basata sulle competenze e sugli sviluppi degli studenti.

È possibile scaricare l'applicazione dal Google Play Store e dall'Apple App Store.

Sì, hai accesso completamente gratuito a tutti i contenuti nell'app e puoi chattare o seguire i Creatori in qualsiasi momento. Sbloccherai nuove funzioni crescendo il tuo numero di follower. Inoltre, offriamo Knowunity Premium, che consente di studiare senza alcun limite!!

Studio Completo di Funzione: Guida per Studenti

Dominio e prime analisi

Limiti e asintoti

Derivate e studio della funzione

Pensavamo che non l'avreste mai chiesto....

Che cos'è l'assistente AI di Knowunity?

Dove posso scaricare l'applicazione Knowunity?

Knowunity è davvero gratuita?

Contenuti simili

𝐷𝑒𝑟𝑖𝑣𝑎𝑡𝑒

MATEMATICA: Derivate

Derivate

Regole di Derivazione

Derivate

Formulario matematica

Contenuti più popolari: Regole di Differenziazione

Formulario matematica

Regole di Derivazione

Derivate

𝐷𝑒𝑟𝑖𝑣𝑎𝑡𝑒

Derivate

Contenuti più popolari: Matematica

Prima parte programma matematica test professioni sanitarie

Preparazione Matrmatica TOLC-E

Formulario mate TOLC PSI

Funzioni

Prodotti notevoli

Preparazione Tolc I

LIMITI - APPUNTI COMPLETI CON TEOREMI

Formulario di mate

Disequazioni

Contenuti più popolari

Teoria patente di guida B: Segnali stradali

Riassunto patente B

Patente

appunti patente

Patente B

Prima parte programma biologia test professioni sanitarie

Patente B / A

Tutta la patente B

MANUALE PATENTE A & B SCHEMATICO

Recensioni dei nostri utenti. Ci adorano - e anche tu, vedrai .