Classificazione delle Funzioni

Le funzioni algebriche si dividono in diverse categorie che devi imparare a riconoscere subito. Quelle razionali intere come f(x) = x²-3x+1 hanno dominio su tutti i reali (ℝ), quindi sono le più semplici da gestire.

Le funzioni razionali fratte invece richiedono più attenzione. Per esempio, con g(x) = $3x+1$/$2-x$, devi assicurarti che il denominatore non sia mai zero: 2-x ≠ 0, quindi x ≠ 2. Il dominio diventa quindi ℝ-{2} o (-∞;2)∪(2;+∞).

Per le funzioni irrazionali con radici pari, ricorda che l'argomento sotto radice deve essere ≥ 0. Se hai √$x-1$, allora x-1 ≥ 0, quindi x ≥ 1 e il dominio è [1;+∞).

Trucco memoria: Razionali fratte → denominatore ≠ 0; Radici pari → argomento ≥ 0!

Funzioni con Valore Assoluto

Le funzioni con valore assoluto combinano spesso più condizioni. Quando hai f(x) = $|x+3|-5$/√$x-2$, devi risolvere un sistema di condizioni.

Prima risolvi |x+3|-5 ≠ 0, che significa |x+3| ≠ 5. Questo ti dà x+3 ≠ ±5, quindi x ≠ 2 e x ≠ -8. Poi aggiungi la condizione per la radice: x-2 > 0, quindi x > 2.

Il dominio finale sarà l'intersezione di tutte le condizioni: (-∞;-8)∪(-8;2)∪(2;+∞), escludendo però i punti dove x ≤ 2. Quindi ottieni (2;+∞) escluso eventuali altri punti problematici.

Le radici con indice dispari invece non hanno restrizioni sull'argomento - possono avere valori negativi sotto radice!

Esercizi Pratici Risolti

Negli esercizi del libro, imparerai a gestire casi sempre più complessi. Per y = $x-5$/$x³+x+2$, devi fattorizzare il denominatore: x³+x+2 = $x+1$$x²-x+2$.

Quindi risolvi $x+1$$x²-x+2$ ≠ 0. Il primo fattore ti dà x ≠ -1, mentre per il secondo fattore calcoli il discriminante: Δ = 1-8 = -7 < 0, quindi x²-x+2 > 0 sempre.

Per funzioni composte con radici multiple come y = √$(x²-4)/(x-3)$ + √$1-√x$, devi risolvere separatamente ogni parte. La prima richiede $x²-4$/$x-3$ ≥ 0 e x ≠ 3, la seconda richiede x ≥ 0 e 1-√x ≥ 0.

Strategia vincente: Affronta sempre una condizione alla volta, poi trova l'intersezione finale!

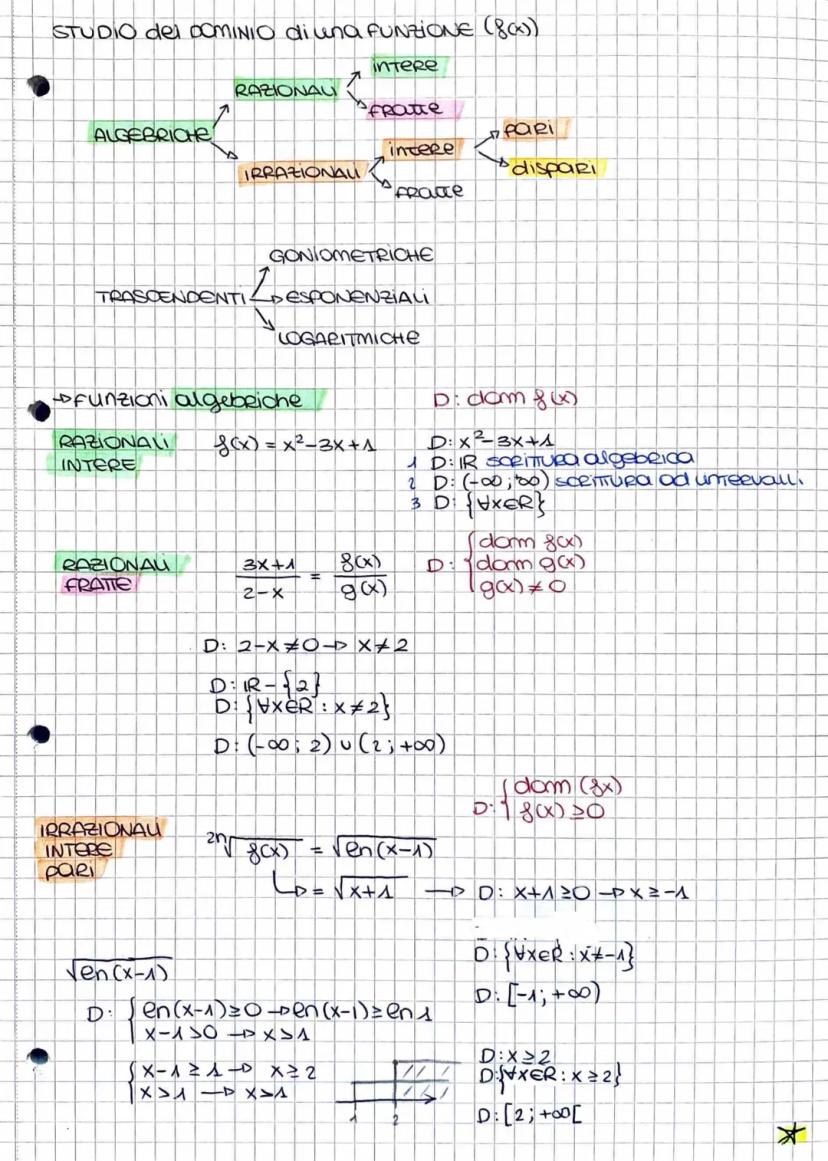
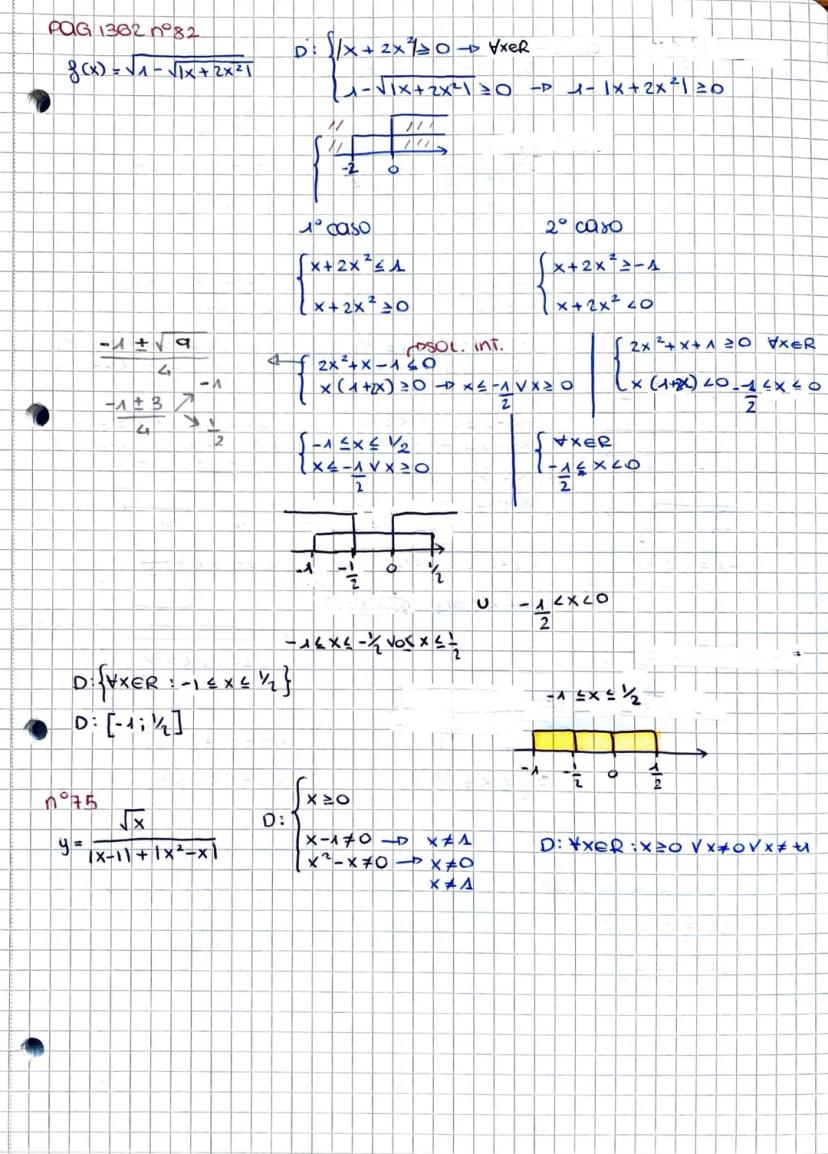
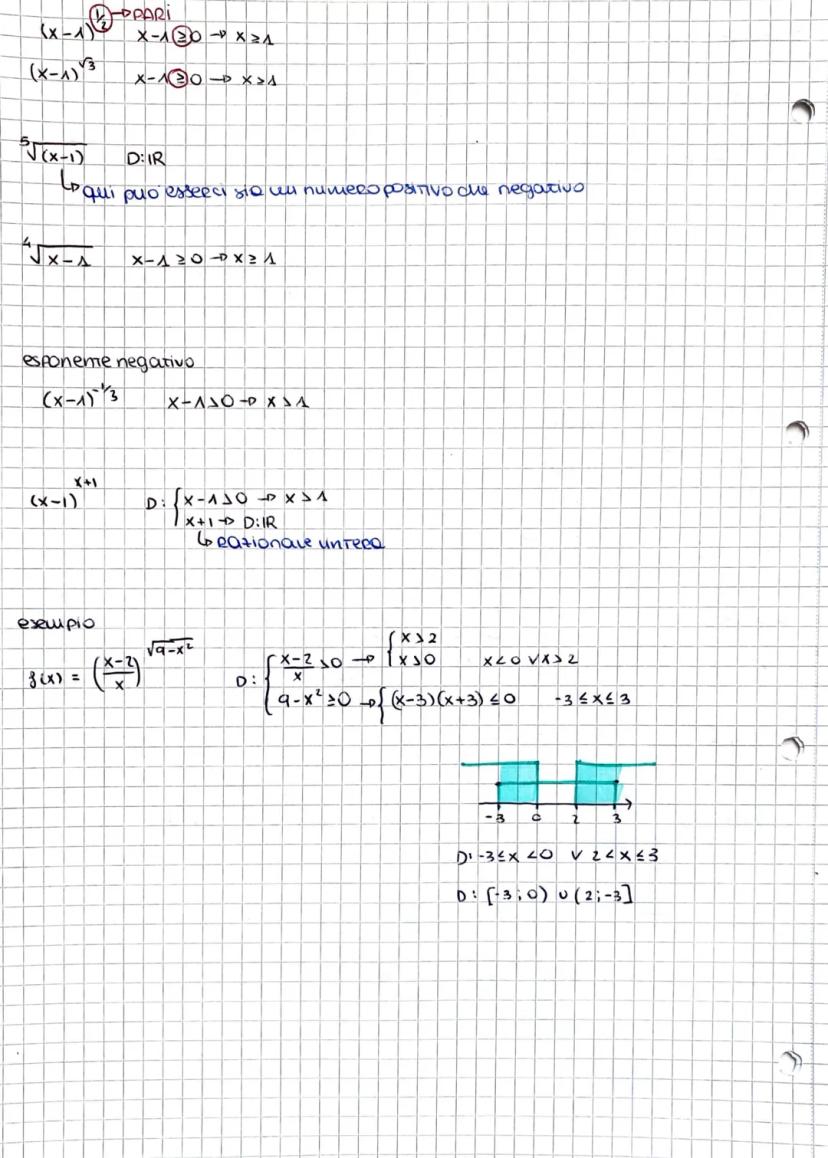
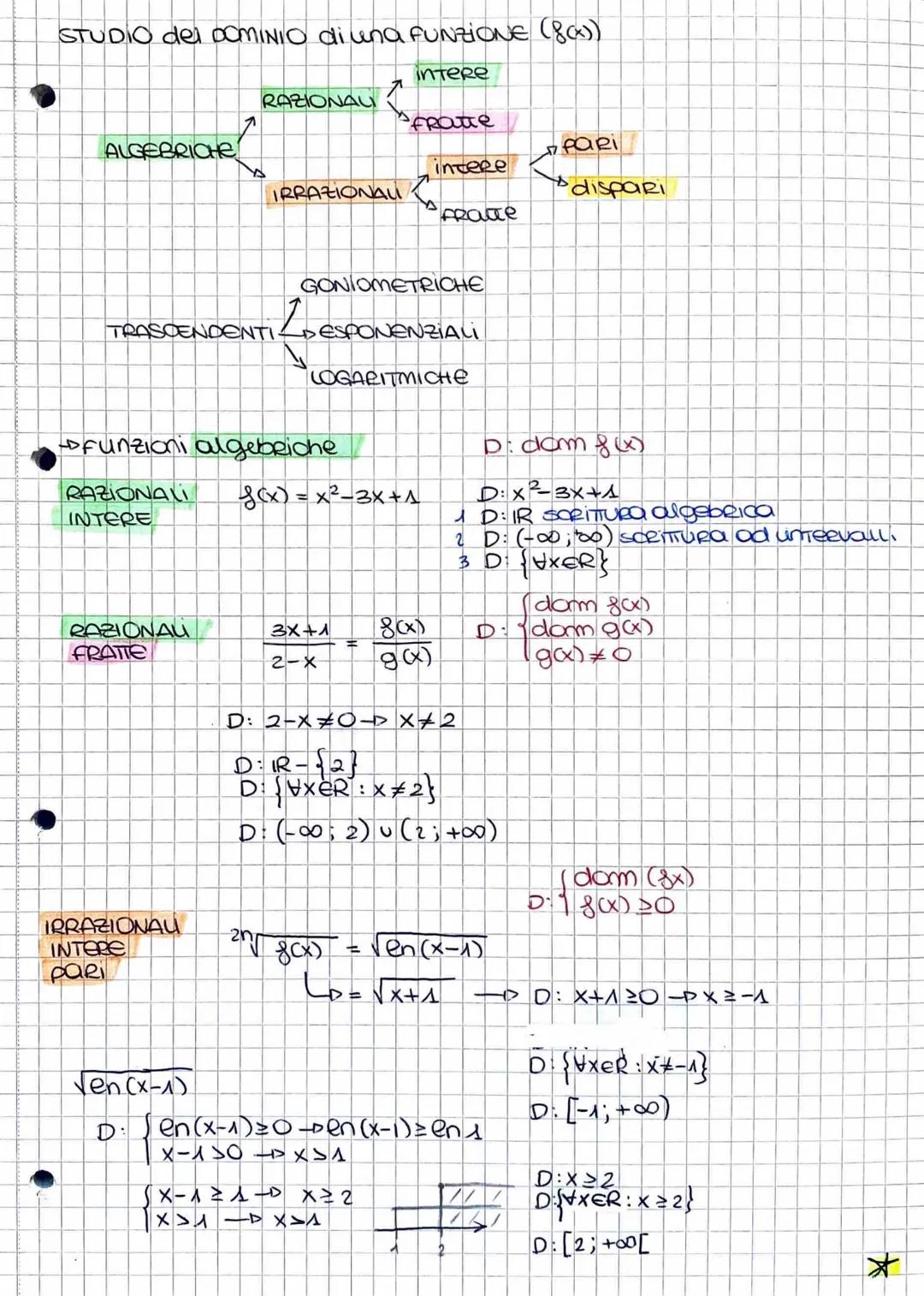
Domini con Intersezioni

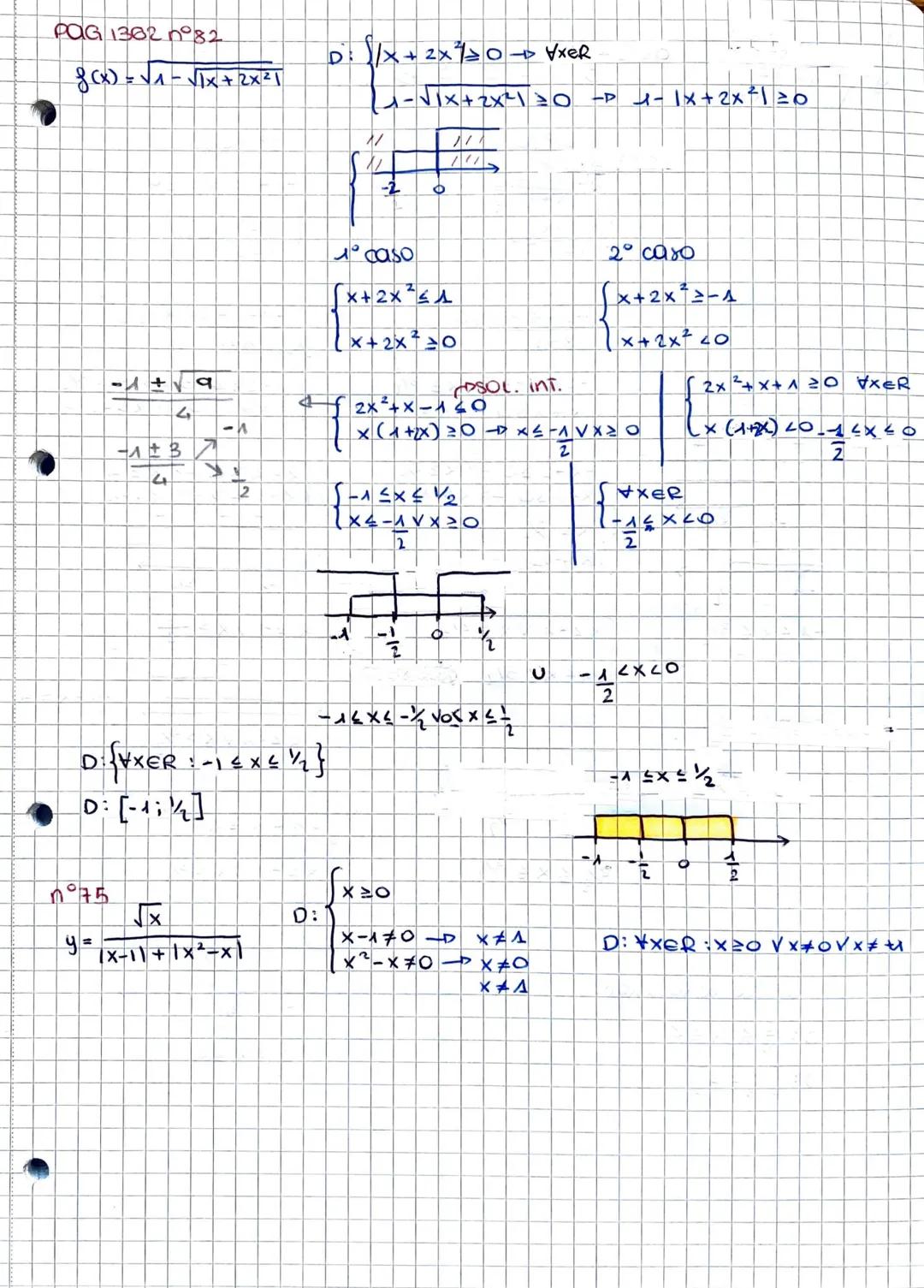
Quando hai più condizioni simultanee, devi trovare l'intersezione tra tutti i domini parziali. Nell'esercizio con le due radici, hai ottenuto D₁: -2 ≤ x ≤ 2 ∨ x > 3 e D₂: 0 ≤ x ≤ 1.

Il dominio finale è l'intersezione: D = $0;1$. Questo significa che la funzione esiste solo quando entrambe le condizioni sono soddisfatte contemporaneamente.

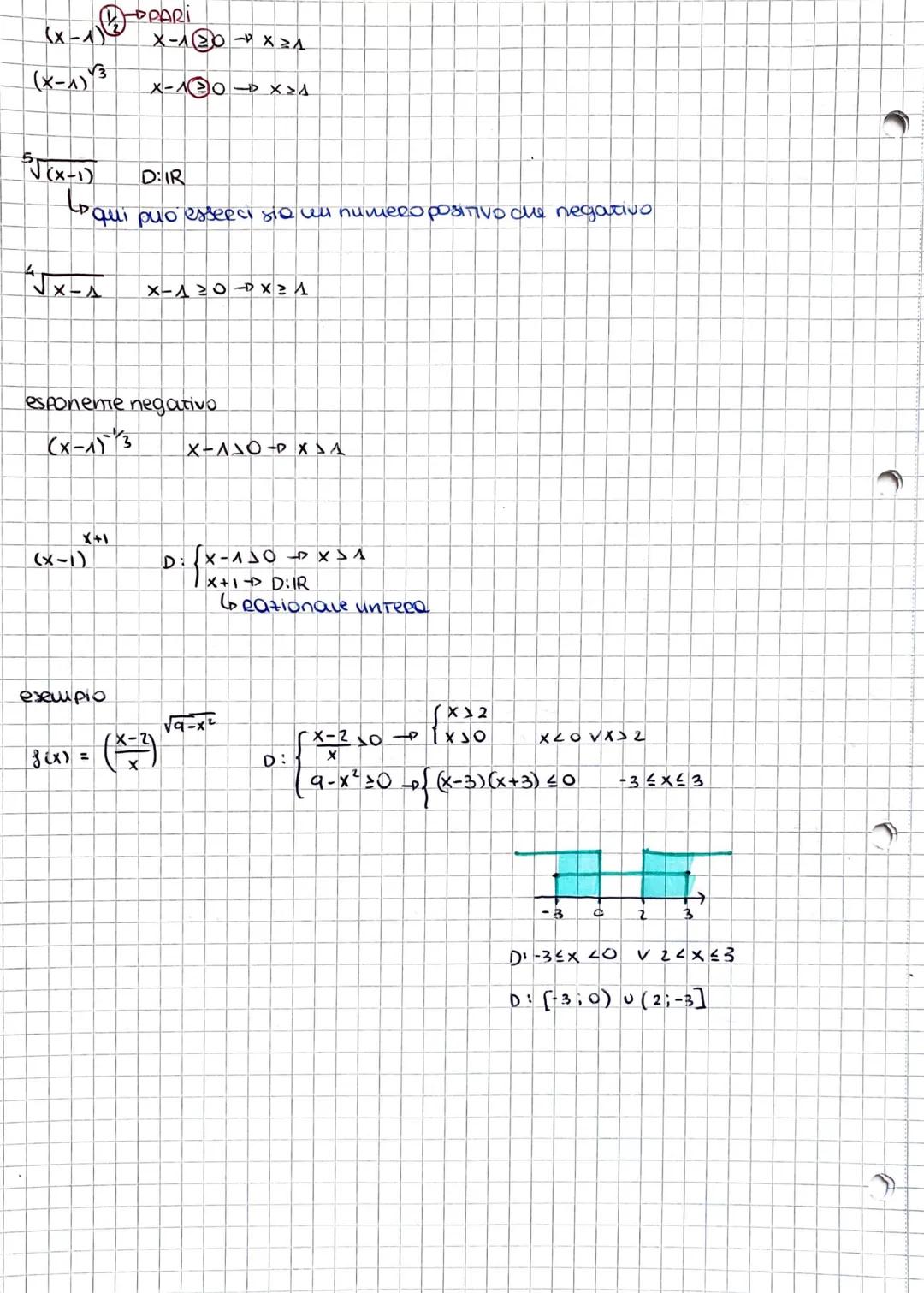
Per funzioni molto complesse come y = √$x⁴-x²-2$/$2x√|x-1|$, devi gestire numeratore ≥ 0, denominatore ≠ 0, e |x-1| > 0. Fattorizzando x⁴-x²-2 con la sostituzione t = x², ottieni le condizioni finali.

Ricorda che x⁴-x²-2 = $x²+1$$x²-2$, dove x²+1 > 0 sempre, quindi ti resta solo x² ≥ 2, cioè |x| ≥ √2.

Funzioni con Radici Annidate

Le funzioni con radici annidate come g(x) = √$1-√(x+2x²)$ richiedono un approccio a strati. Prima risolvi la radice interna: x+2x² ≥ 0, poi quella esterna: 1-√$x+2x²$ ≥ 0.

Per la condizione esterna, devi distinguere due casi basati sul valore assoluto. Se x+2x² ≤ 1 e x+2x² ≥ 0, risolvi il sistema e ottieni parte del dominio.

Fattorizzando 2x²+x-1 ≤ 0 trovi $-1/2 ≤ x ≤ 1/2$, mentre x$2x+1$ ≥ 0 dà $x ≤ -1/2 ∨ x ≥ 0$. L'intersezione ti porta a specifici intervalli.

Metodo infallibile: Con radici annidate, lavora dall'interno verso l'esterno, un livello alla volta!

Il dominio finale è $-1; 1/2$, che comprende tutti i punti dove la funzione è matematicamente definita.

Funzioni Trascendenti: Esponenziali e Logaritmi

Le funzioni trascendenti hanno regole di dominio specifiche che devi memorizzare. Per y = a^(g(x)), il dominio coincide con quello di g(x) - non ci sono restrizioni aggiuntive sull'esponente.

I logaritmi sono più selettivi: per y = log_a g(x), serve g(x) > 0. Se hai un logaritmo con base variabile y = log_(g(x)) f(x), devi rispettare tre condizioni: f(x) > 0, g(x) > 0, e g(x) ≠ 1.

Per gli esempi pratici: f(x) = e^$1/x$ ha dominio ℝ-{0} perché l'esponente 1/x non può avere denominatore nullo. Invece f(x) = ln$x/(x+2)$ richiede x/$x+2$ > 0, che significa x < -2 ∨ x > 0.

Le funzioni del tipo f(x)^(g(x)) richiedono f(x) > 0 e che g(x) sia nel suo dominio naturale.

Regola d'oro: Logaritmi → argomento positivo; Esponenziali → nessuna restrizione aggiuntiva!

Funzioni con Esponenti Razionali

Quando hai esponenti razionali come $x-1$^(2/3), devi fare attenzione al segno della base. Se l'esponente ha denominatore pari, la base deve essere ≥ 0 per evitare problemi con numeri complessi.

Per funzioni come f(x) = √$9-x²$, risolvi 9-x² ≥ 0, che diventa $3-x$$3+x$ ≥ 0. Usando il metodo dei segni, ottieni -3 ≤ x ≤ 3.

Le combinazioni complesse richiedono l'intersezione di più condizioni. Se hai radici e frazioni insieme, risolvi separatamente ogni vincolo, poi trova dove si sovrappongono.

Negli esercizi più difficili, potresti avere sistemi come -3 ≤ x ≤ 3 combinato con x ≠ 2 e x ≠ 3, che ti porta a domini come [-3;0)∪(2;3).

Funzioni Goniometriche e Inverse

Le funzioni goniometriche hanno domini specifici da ricordare. Per f(x) = tan(g(x)), devi evitare g(x) = π/2 + kπ. Per f(x) = cot(g(x)), escludi g(x) = kπ.

Le funzioni goniometriche inverse hanno restrizioni sull'argomento: arcsin e arccos richiedono -1 ≤ argomento ≤ 1. Quindi per f(x) = arcsin$x-1$, devi risolvere -1 ≤ x-1 ≤ 1, ottenendo 0 ≤ x ≤ 2.

Per combinazioni complesse come f(x) = tan(ln x), unisci le condizioni: ln x ≠ π/2 + kπ $quindi x ≠ e^(π/2+kπ)$ e x > 0 per il logaritmo.

Negli esercizi con funzioni composte tipo f(x) = $arcsin(x-1)$², devi rispettare sia il dominio dell'arcsin che la condizione per l'elevamento a potenza.

Memo veloce: tan e cot → escludi multipli di π; arcsin e arccos → argomento tra -1 e 1!