Insiemi, Numeri Naturali e Criteri di Divisibilità

Gli insiemi sono semplicemente raccolte di elementi che seguono una regola precisa. Pensa a un insieme come a un contenitore dove metti oggetti che hanno qualcosa in comune. Il simbolo ∈ significa "appartiene a", mentre ∉ significa "non appartiene a".

Le operazioni tra insiemi più importanti sono l'intersezione (∩) che ti dà gli elementi comuni, e l'unione (∪) che raccoglie tutti gli elementi di entrambi. Per esempio: se A={0,3,8} e B={0,3,22,40}, allora A∩B={0,3}.

I numeri naturali hanno regole precise per le operazioni. Ricorda sempre l'ordine di priorità: prima le parentesi, poi potenze e radici, quindi moltiplicazioni e divisioni, infine addizioni e sottrazioni. I criteri di divisibilità ti faranno risparmiare un sacco di tempo: un numero è divisibile per 2 se l'ultima cifra è pari, per 3 se la somma delle cifre è divisibile per 3, per 5 se finisce con 0 o 5.

Trucco per gli esami: I criteri di divisibilità sono spesso richiesti nei test d'ingresso universitari!

Numeri Relativi, Frazioni e Percentuali

I numeri relativi includono positivi, negativi e lo zero. Il valore assoluto |a| è sempre positivo: se il numero è già positivo resta uguale, se è negativo diventa positivo.

Le operazioni con le frazioni seguono regole precise. Per sommare o sottrarre, trova il m.c.m. dei denominatori. Per moltiplicare, moltiplica numeratori tra loro e denominatori tra loro. Per dividere, moltiplica per il reciproco della seconda frazione.

Le percentuali sono ovunque nella vita reale! Il 25% si scrive come 25/100 = 0,25. Per calcolare uno sconto: prezzo × percentuale/100. Per gli interessi: Capitale × Tempo × Tasso. La variazione percentuale si calcola con: (valore nuovo - valore vecchio)/valore vecchio × 100%.

Consiglio pratico: Le percentuali sono fondamentali per economia, fisica e problemi di vita quotidiana!

Prodotti Notevoli, Polinomi e Radicali

I prodotti notevoli sono formule che devi sapere a memoria perché ti velocizzano tantissimo i calcoli. I più importanti: $a+b$² = a²+2ab+b², $a-b$² = a²-2ab+b², a+b$$a-b = a²-b².

La scomposizione in fattori trasforma una somma in un prodotto. Il raccoglimento a fattore comune cerca l'elemento comune: 15x³+25x²+5x = 5x$3x²+5x+1$. Per il raccoglimento parziale, raggruppa i termini strategicamente.

I radicali rappresentano le radici. Attenzione ai casi: se l'indice è pari e il radicando è negativo, non esiste nel campo reale. Le operazioni: √a·√b = √(ab), √a/√b = √(a/b). Per sommare i radicali devono essere simili: 3√3 + 2√3 = 5√3.

Trucco fondamentale: Il triangolo di Tartaglia ti dà i coefficienti delle potenze di $a+b$ⁿ senza dover calcolare tutto!

Potenze Frazionarie, Razionalizzazione ed Equazioni

Le potenze con esponente frazionario seguono la regola: a^(m/n) = ⁿ√$a^m$. Questo collega potenze e radicali in modo elegante.

La razionalizzazione elimina i radicali dal denominatore. Per 1/√a moltiplica per √a/√a. Per denominatori più complessi come √a - √b, usa il coniugato $√a + √b$.

Le equazioni di secondo grado incomplete hanno forme speciali. Se manca il termine c (equazione spuria): ax² + bx = 0, scomponi x$ax+b$ = 0. Se manca il termine b (equazione pura): ax² + c = 0, quindi x² = -c/a.

I sistemi di equazioni si risolvono con tre metodi: sostituzione, confronto, riduzione. Il metodo di riduzione è spesso il più veloce: elimini una variabile sommando o sottraendo le equazioni.

Strategia per i compiti: Nelle equazioni incomplete, riconosci subito il tipo per applicare il metodo più rapido!

Sistemi di Equazioni e Disequazioni

Un sistema può essere determinato (una soluzione), indeterminato (infinite soluzioni) o impossibile (nessuna soluzione). Puoi capirlo prima di risolverlo confrontando i coefficienti delle equazioni.

Le disequazioni si rappresentano graficamente con intervalli. x < a si scrive $-∞; a$, x ≥ b si scrive [b; +∞). Attenzione alle parentesi: tonde per "minore/maggiore", quadre per "minore o uguale/maggiore o uguale".

Per le disequazioni di secondo grado, studia il segno del trinomio ax²+bx+c. Se Δ > 0 hai due radici x₁ e x₂: la parabola è positiva esternamente alle radici se a > 0. Le disequazioni frazionarie richiedono lo studio separato di numeratore e denominatore.

Attenzione cruciale: Nel denominatore devi sempre avere il segno strettamente positivo o negativo (mai uguale a zero)!

Logaritmi ed Esponenziali

Il logaritmo è l'operazione inversa dell'elevamento a potenza. log_a b = x significa che a^x = b. Per esempio: log₂ 8 = 3 perché 2³ = 8.

I logaritmi esistono solo se: base > 0, base ≠ 1, argomento > 0. Regole fondamentali: log_a 1 = 0, log_a a = 1. I teoremi sui logaritmi: log_a(bc) = log_a b + log_a c, log_a(b/c) = log_a b - log_a c, log_a$b^m$ = m·log_a b.

I logaritmi naturali (ln) hanno base e ≈ 2,718, quelli decimali (log) hanno base 10. Il cambio di base: log_a b = log_c b / log_c a ti permette di passare da un sistema all'altro.

Le equazioni logaritmiche del tipo log_a f$x$ = b si risolvono con f$x$ = a^b. Per equazioni con più logaritmi, usa le proprietà per ridurle alla forma log_a f$x$ = log_a g$x$, quindi f$x$ = g$x$.

Tip per la calcolatrice: ln è il tasto per i logaritmi naturali, log per quelli decimali!

Disequazioni Logaritmiche ed Esponenziali

Le disequazioni logaritmiche seguono tre passi fondamentali: trova le condizioni di esistenza, riduci alla forma log_a f$x$ < log_a g$x$, risolvi considerando che se a > 1 il verso rimane uguale, se 0 < a < 1 si inverte.

Attenzione al verso! Con base maggiore di 1: log₂ x > log₂ 3 diventa x > 3. Con base minore di 1: log₁/₂ x > log₁/₂ 3 diventa x < 3. È il comportamento crescente/decrescente della funzione logaritmica.

Per le disequazioni esponenziali del tipo a^f$x$ < b^g$x$, applica il logaritmo naturale ad entrambi i membri: ln$a^f(x)$ < ln$b^g(x)$, quindi f$x$·ln a < g$x$·ln b.

Combina sempre le soluzioni ottenute con le condizioni di esistenza attraverso un sistema. Le soluzioni finali sono l'intersezione tra le due condizioni.

Errore comune: Non dimenticare mai di controllare le condizioni di esistenza alla fine!

Geometria Analitica: Rette e Coniche

La geometria analitica unisce algebra e geometria attraverso le coordinate. La distanza tra due punti è √$(x₂-x₁)²+(y₂-y₁)²$, il punto medio è $(x₁+x₂)/2; (y₁+y₂)/2$.

L'equazione generale della retta è ax + by + c = 0. Casi speciali: se a = 0 hai y = k (parallela all'asse x), se b = 0 hai x = k (parallela all'asse y), se c = 0 passa per l'origine. Il coefficiente angolare m determina l'inclinazione.

Le coniche (circonferenza, ellisse, parabola, iperbole) hanno equazioni caratteristiche. La circonferenza x² + y² + ax + by + c = 0 ha centro C$-a/2; -b/2$ e raggio r = √$(a/2)² + (b/2)² - c$. L'ellisse ha equazione x²/a² + y²/b² = 1.

La posizione reciproca di retta e circonferenza dipende dalla distanza dal centro: d > r (esterna), d = r (tangente), d < r (secante).

Formula salvavita: La distanza punto-retta |ax₀+by₀+c|/√$a²+b²$ è fondamentale per tutti gli esercizi!

Parabola, Iperbole e Introduzione alle Funzioni

La parabola y = ax² + bx + c ha vertice V$-b/2a; -Δ/4a$ e asse di simmetria x = -b/2a. Se a > 0 ha la "bocca" verso l'alto, se a < 0 verso il basso. La parabola con asse verticale è sempre una funzione, quella con asse orizzontale no.

L'iperbole x²/a² - y²/b² = 1 ha fuochi F₁$-c,0$ e F₂(c,0) con c² = a² + b². Gli asintoti sono y = ±(b/a)x. L'iperbole equilatera ha equazione x² - y² = a² e asintoti perpendicolari y = ±x.

Per riconoscere le coniche dall'equazione generale Ax² + Bxy + Cy² + Dx + Ey + F = 0, calcola Δ = B² - 4AC: se Δ < 0 è un'ellisse, se Δ = 0 è una parabola, se Δ > 0 è un'iperbole.

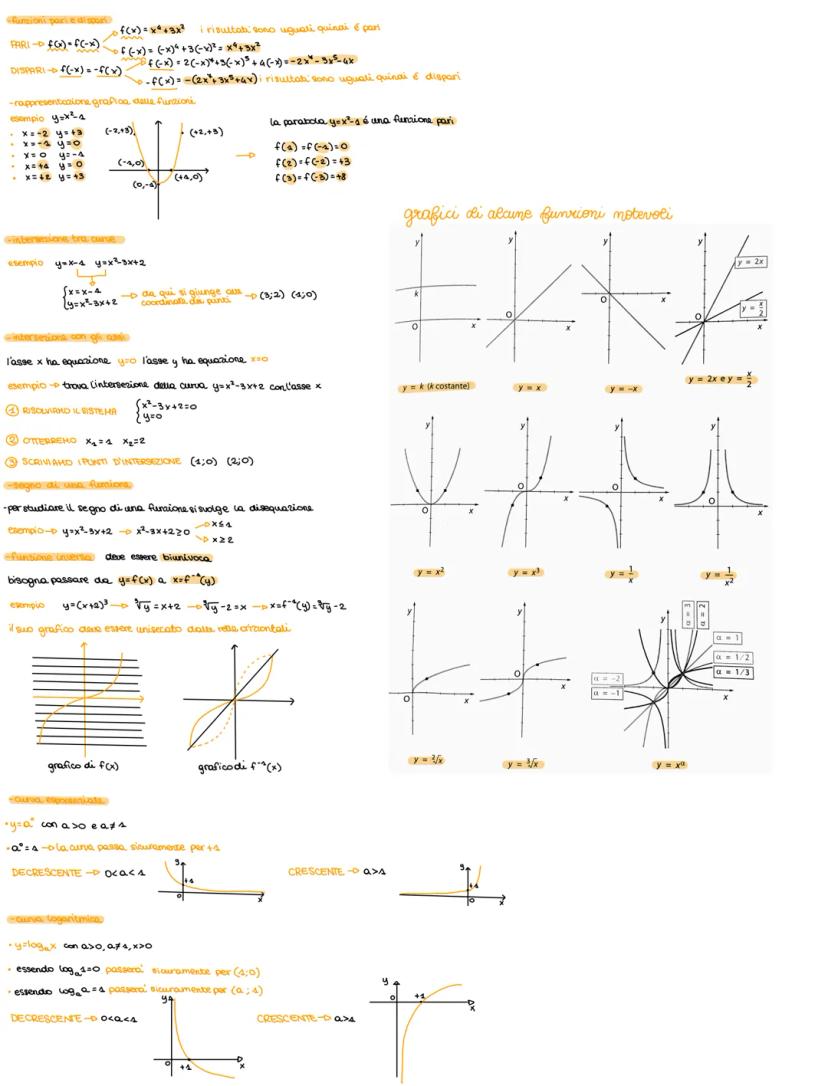
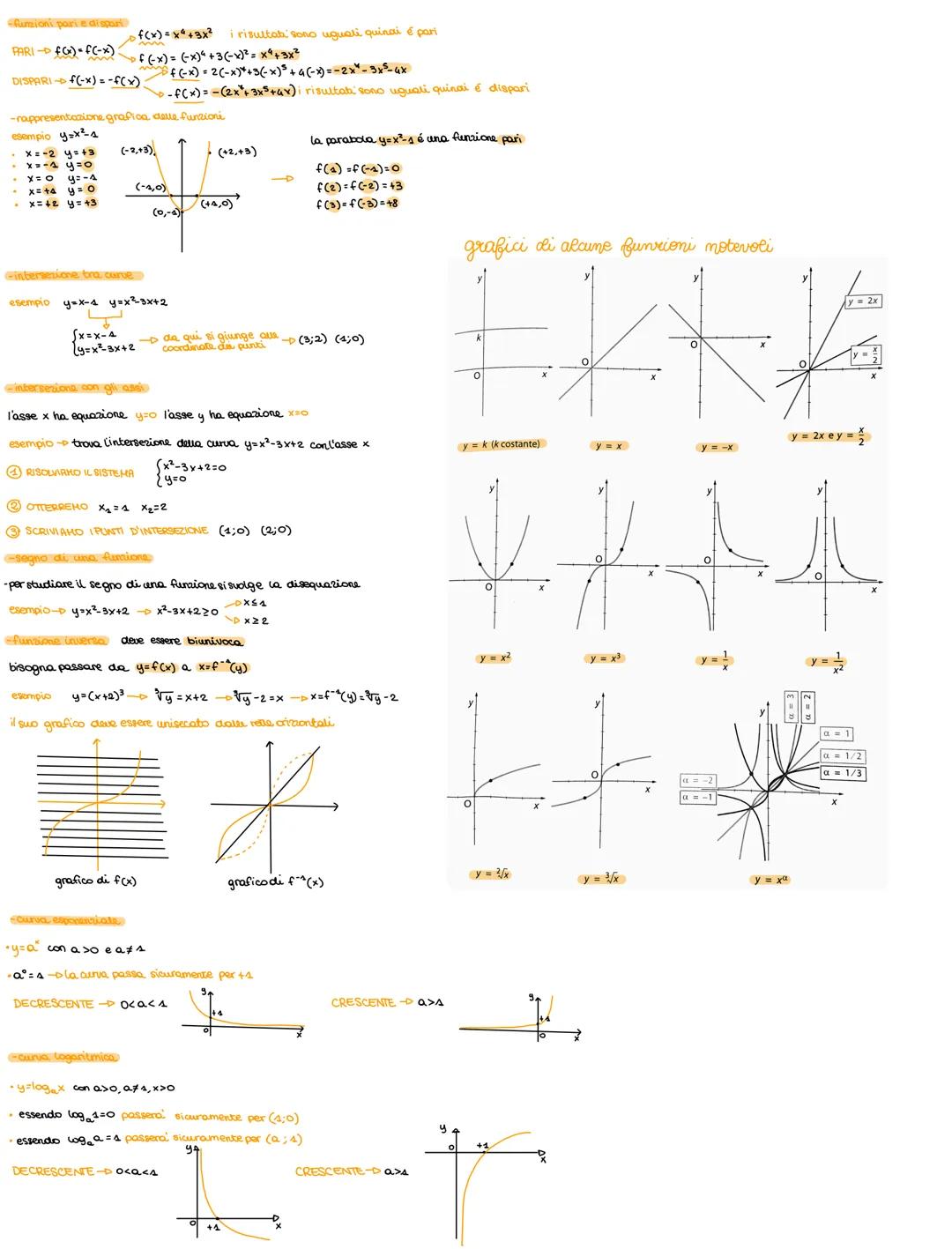
Le funzioni collegano ogni elemento del dominio X a un elemento del codominio Y. Possono essere iniettive (elementi distinti hanno immagini distinte), suriettive (ogni elemento di Y è immagine di qualche elemento di X), biiettive (entrambe le proprietà).

Trucco per gli esercizi: Il discriminante Δ = B² - 4AC ti dice subito che conica stai studiando!

Studio delle Funzioni e Grafici

Il dominio (o campo di esistenza) è l'insieme dei valori di x per cui la funzione è definita. Funzioni razionali intere: x ∈ ℝ. Razionali fratte: denominatore ≠ 0. Irrazionali: argomento ≥ 0. Logaritmiche: argomento > 0.

Una funzione è pari se f$-x$ = f$x$ (simmetrica rispetto all'asse y), dispari se f$-x$ = -f$x$ (simmetrica rispetto all'origine). Una funzione è crescente se al crescere di x cresce anche f$x$, decrescente nel caso contrario.

Per trovare le intersezioni con gli assi: con l'asse x poni y = 0, con l'asse y poni x = 0. Il segno della funzione si studia risolvendo f$x$ ≥ 0.

Le funzioni esponenziali y = aˣ passano sempre per (0,1). Se a > 1 sono crescenti, se 0 < a < 1 sono decrescenti. Le funzioni logaritmiche y = log_a x passano per (1,0) e (a,1), con comportamento opposto alle esponenziali.

Strategia di studio: Per ogni funzione, trova sempre dominio, intersezioni, segno e comportamento - sono i pilastri del grafico!