Matematica

Equazioni delle Sezioni Coniche

Equazione dell'Iperbole

Matematica1248Aggiornato 10 set 20264 pagine

L'Iperbole: Definizione e Proprietà

Segnala

ehilà@ehi6732821687873

Aggiungi alle fonti Google

L'iperbole è una delle curve più affascinanti della geometria analitica che incontrerai spesso nei problemi di matematica. Si tratta del luogo geometrico dei punti per cui la differenza delle distanze da due fuochi è sempre costante, e ha proprietà uniche che la rendono diversa da parabole e ellissi.

Iscriviti per mostrare il contenuto.
È gratis!

Accesso a tutti i documenti
Migliora i tuoi voti
Unisciti a milioni di studenti

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Definizione e caratteristiche fondamentali dell'iperbole

Immagina l'iperbole come una curva formata da punti che mantengono sempre la stessa differenza di distanza da due punti fissi chiamati fuochi (F₁ e F₂). Matematicamente scriviamo: |PF₁ - PF₂| = costante = 2a.

La forma dell'iperbole dipende da dove si trovano i fuochi. Se i fuochi stanno sull'asse delle x, l'equazione canonica è x²/a² - y²/b² = 1. Se invece stanno sull'asse delle y, diventa y²/a² - x²/b² = 1.

I parametri fondamentali sono il semiasse trasverso $a$ e quello non trasverso $b$ , mentre c rappresenta la semidistanza focale. La relazione che li lega è sempre c² = a² + b².

Trucco per ricordare: L'iperbole "si apre" nella direzione dell'asse dove trovi il termine positivo nell'equazione canonica!

Gli asintoti sono le rette y = ±(b/a)x che l'iperbole si avvicina all'infinito senza mai toccare. L'eccentricità e = c/a è sempre maggiore di 1, distinguendo l'iperbole dalle altre coniche.

Iscriviti per mostrare il contenuto.
È gratis!

Accesso a tutti i documenti
Migliora i tuoi voti
Unisciti a milioni di studenti

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

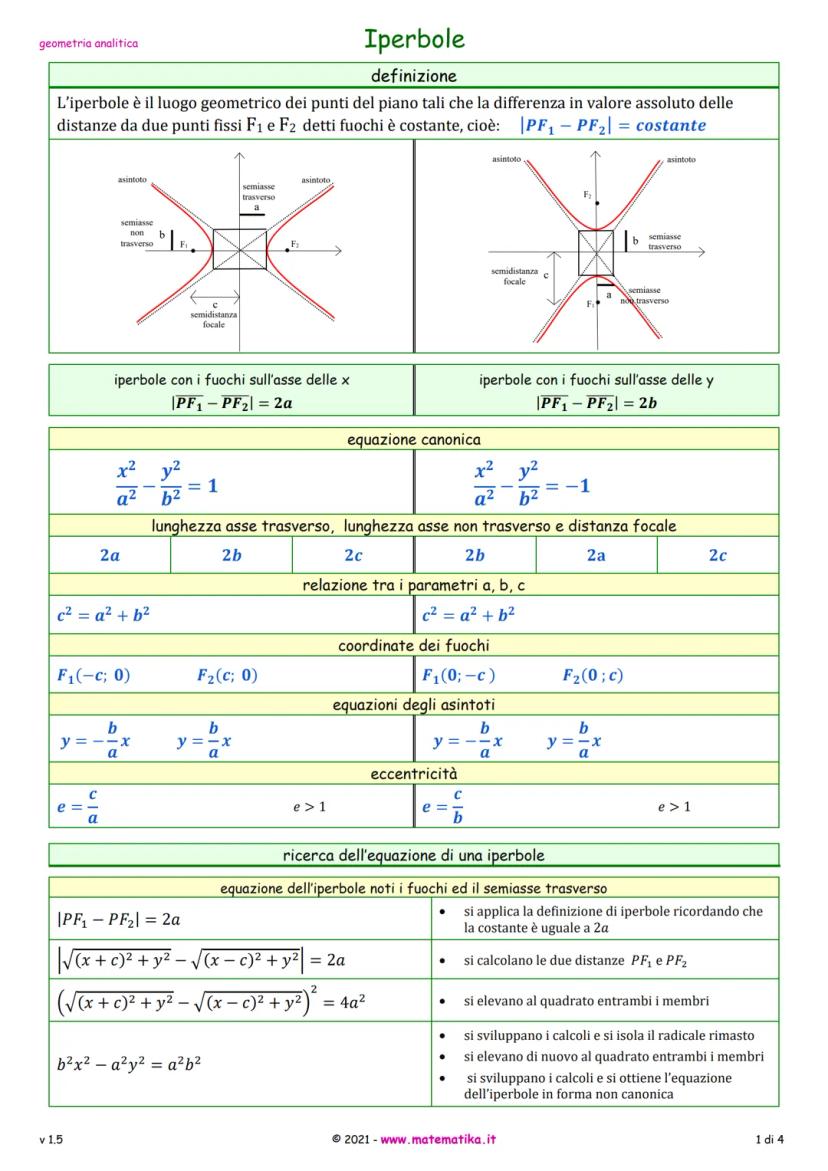
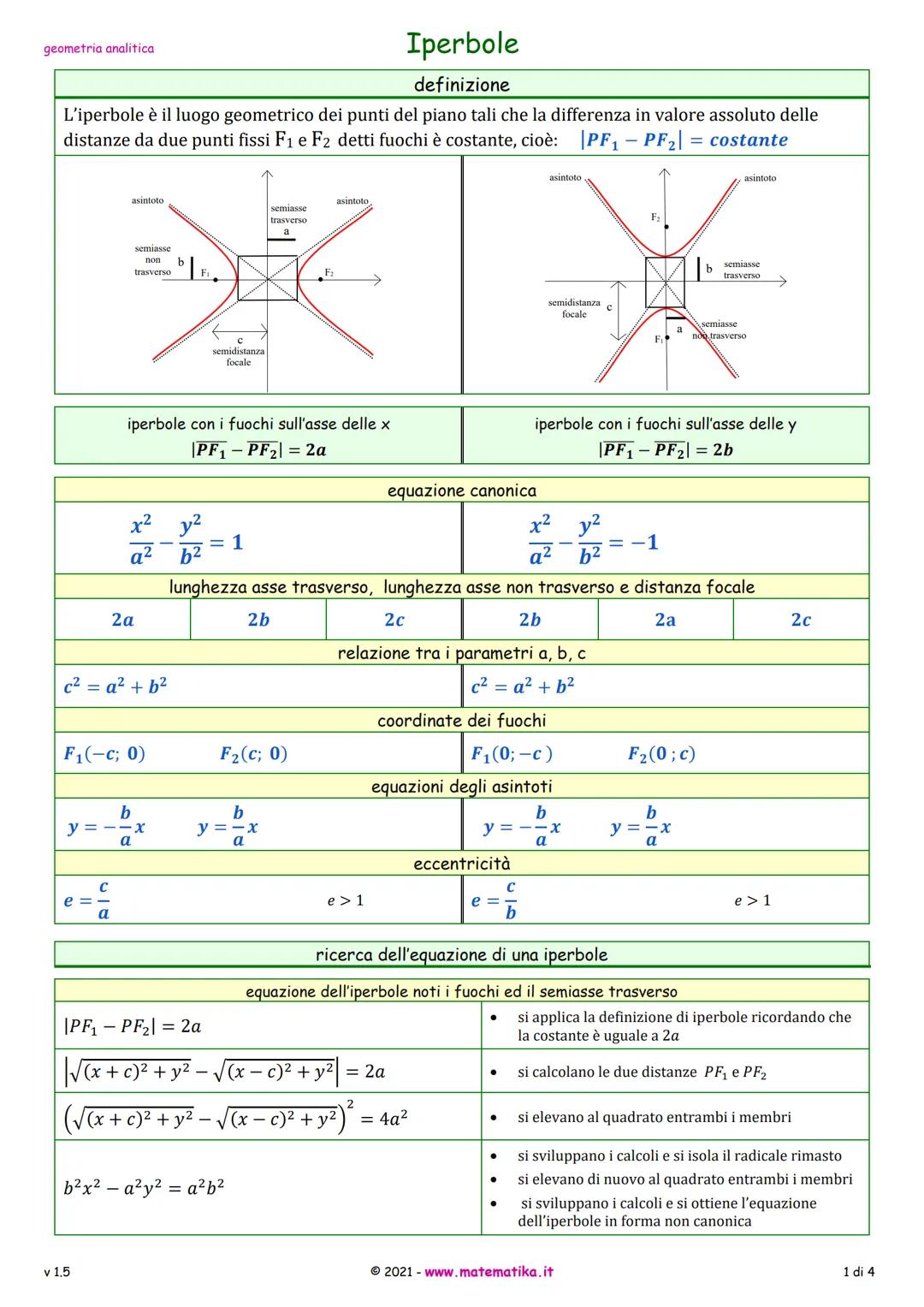
Come trovare l'equazione dell'iperbole

Trovare l'equazione di un'iperbole è come risolvere un puzzle: devi sempre avere almeno due informazioni (fuochi, semiassi, punti di passaggio, eccentricità).

Quando conosci i fuochi e il semiasse trasverso, applichi direttamente la definizione |PF₁ - PF₂| = 2a. Calcoli le distanze, elevi al quadrato due volte (attenzione ai calcoli!) e ottieni l'equazione canonica.

Per un'iperbole che passa per due punti A(x₁, y₁) e B(x₂, y₂), sostituisci le coordinate nell'equazione αx² - βy² = 1. Questo ti dà un sistema di due equazioni nelle incognite α e β, che risolvi per trovare a² e b².

Attenzione: Le incognite sono sempre a² e b², non a e b! Questo errore costa punti negli esami.

Per le rette tangenti, hai diverse strategie. Da un punto esterno usi il fascio proprio, imponi la condizione di tangenza $Δ = 0$ e risolvi. Se il punto sta sull'iperbole, usi la formula di sdoppiamento: sostituisci x² con x₀x e y² con y₀y.

Iscriviti per mostrare il contenuto.
È gratis!

Accesso a tutti i documenti
Migliora i tuoi voti
Unisciti a milioni di studenti

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Rette tangenti e iperbole traslata

Le rette tangenti con coefficiente angolare m assegnato si trovano scrivendo y = mx + q e sostituendo nell'equazione dell'iperbole. Imponi la condizione di tangenza $Δ = 0$ per trovare i valori di q, ottenendo così le due tangenti parallele.

Questo metodo è particolarmente utile quando devi trovare tangenti parallele o perpendicolari a una retta data. Ricorda che due rette sono perpendicolari quando il prodotto dei loro coefficienti angolari è -1.

L'iperbole traslata ha il centro in un punto O'(α, β) diverso dall'origine. La sua equazione diventa $x-α$ ²/a² - $y-β$ ²/b² = 1. Per trovarla, parti dall'equazione canonica e sostituisci x con $x-α$ e y con $y-β$ .

Consiglio pratico: Quando risolvi problemi con iperboli traslate, identifica prima il centro, poi applica la traslazione. È molto più semplice!

La traslazione non cambia la forma dell'iperbole, solo la sua posizione nel piano. I fuochi si spostano della stessa quantità del centro.

Iscriviti per mostrare il contenuto.
È gratis!

Accesso a tutti i documenti
Migliora i tuoi voti
Unisciti a milioni di studenti

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Iperbole equilatera e funzione omografica

L'iperbole equilatera è un caso speciale dove a = b, cioè i semiassi sono uguali. La sua equazione diventa semplicemente x² - y² = a², e gli asintoti sono le rette y = x e y = -x (le bisettrici dei quadranti).

Nell'iperbole equilatera, l'eccentricità è sempre e = √2, e i fuochi si trovano a distanza c = a√2 dal centro. È una forma molto simmetrica e elegante.

Quando ruoti l'iperbole equilatera di 45°, ottieni l'equazione xy = k. Se k > 0, l'iperbole si trova nel I e III quadrante; se k < 0, nel II e IV quadrante. I fuochi si posizionano in (±√(2k), ±√(2k)).

Collegamento importante: L'iperbole equilatera ruotata e traslata diventa la funzione omografica y = $ax+b$ / $cx+d$ !

La funzione omografica è quindi un'iperbole "mascherata". Ha asintoti verticali $x = -d/c$ e orizzontali $y = a/c$ , e il suo centro è nel punto $-d/c, a/c$ . Questa connessione ti aiuterà molto nello studio delle funzioni.

Pensavamo che non l'avreste mai chiesto....

Il nostro assistente AI è costruito specificamente per le esigenze degli studenti. Sulla base dei milioni di contenuti presenti sulla piattaforma, possiamo fornire agli studenti risposte davvero significative e pertinenti. Ma non si tratta solo di risposte, l'assistente è in grado di guidare gli studenti attraverso le loro sfide quotidiane di studio, con piani di studio personalizzati, quiz o contenuti nella chat e una personalizzazione al 100% basata sulle competenze e sugli sviluppi degli studenti.

È possibile scaricare l'applicazione dal Google Play Store e dall'Apple App Store.

Sì, hai accesso completamente gratuito a tutti i contenuti nell'app e puoi chattare o seguire i Creatori in qualsiasi momento. Sbloccherai nuove funzioni crescendo il tuo numero di follower. Inoltre, offriamo Knowunity Premium, che consente di studiare senza alcun limite!!

L'Iperbole: Definizione e Proprietà

Definizione e caratteristiche fondamentali dell'iperbole

Come trovare l'equazione dell'iperbole

Rette tangenti e iperbole traslata

Iperbole equilatera e funzione omografica

Pensavamo che non l'avreste mai chiesto....

Che cos'è l'assistente AI di Knowunity?

Dove posso scaricare l'applicazione Knowunity?

Knowunity è davvero gratuita?

Contenuti simili

Formulario triennio matematica parte 1

Iperbole - Iperbole equilatera - Funzione omografica

GEOMETRIA ANALITICA

iperbole

formulario retta e coniche

Iperbole

Contenuti più popolari: Equazione dell'Iperbole

GEOMETRIA ANALITICA

Iperbole

formulario retta e coniche

Iperbole - Iperbole equilatera - Funzione omografica

Contenuti più popolari: Matematica

Prima parte programma matematica test professioni sanitarie

Formulario mate TOLC PSI

Preparazione Matrmatica TOLC-E

Preparazione Tolc I

Seconda parte programma matematica test professioni sanitarie

Formulario di mate

Tolc - simulazione sezione di logica - ingegneria

Prodotti notevoli

I logaritmi e le equazioni e disequazioni logaritmiche

Contenuti più popolari

Riassunto patente B

Teoria patente b

appunti patente

Teoria patente di guida B: Segnali stradali

Patente B

Prima parte programma biologia test professioni sanitarie

Patente

Programma chimica test professioni sanitarie

🚗 Teoria Patente B Completa + Errori Frequenti Quiz 2026

Recensioni dei nostri utenti. Ci adorano - e anche tu, vedrai .