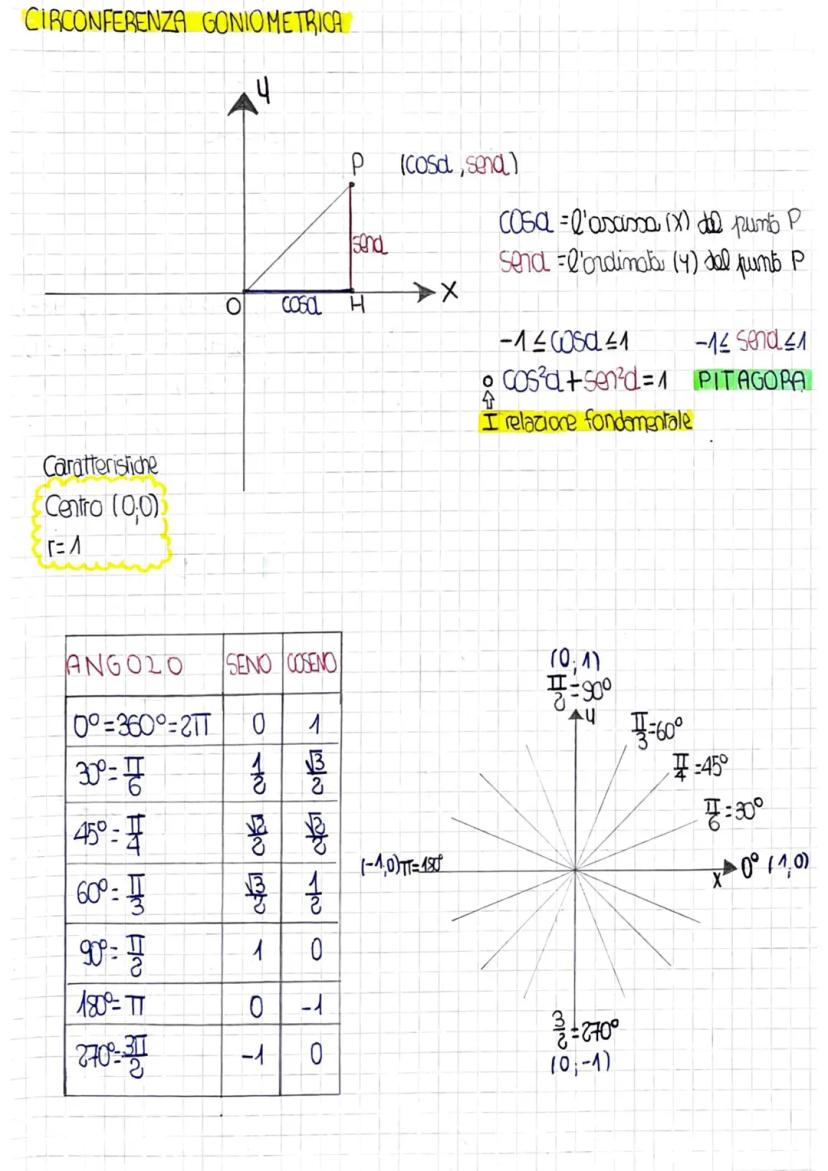
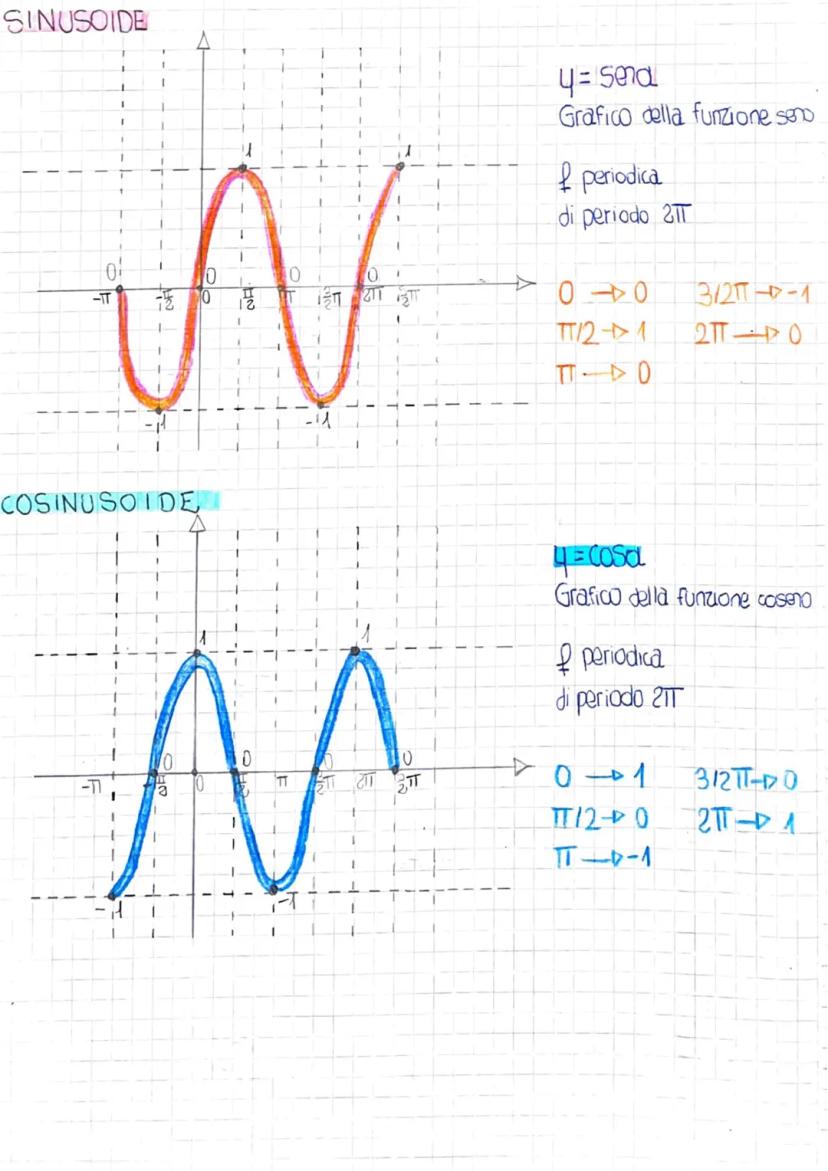
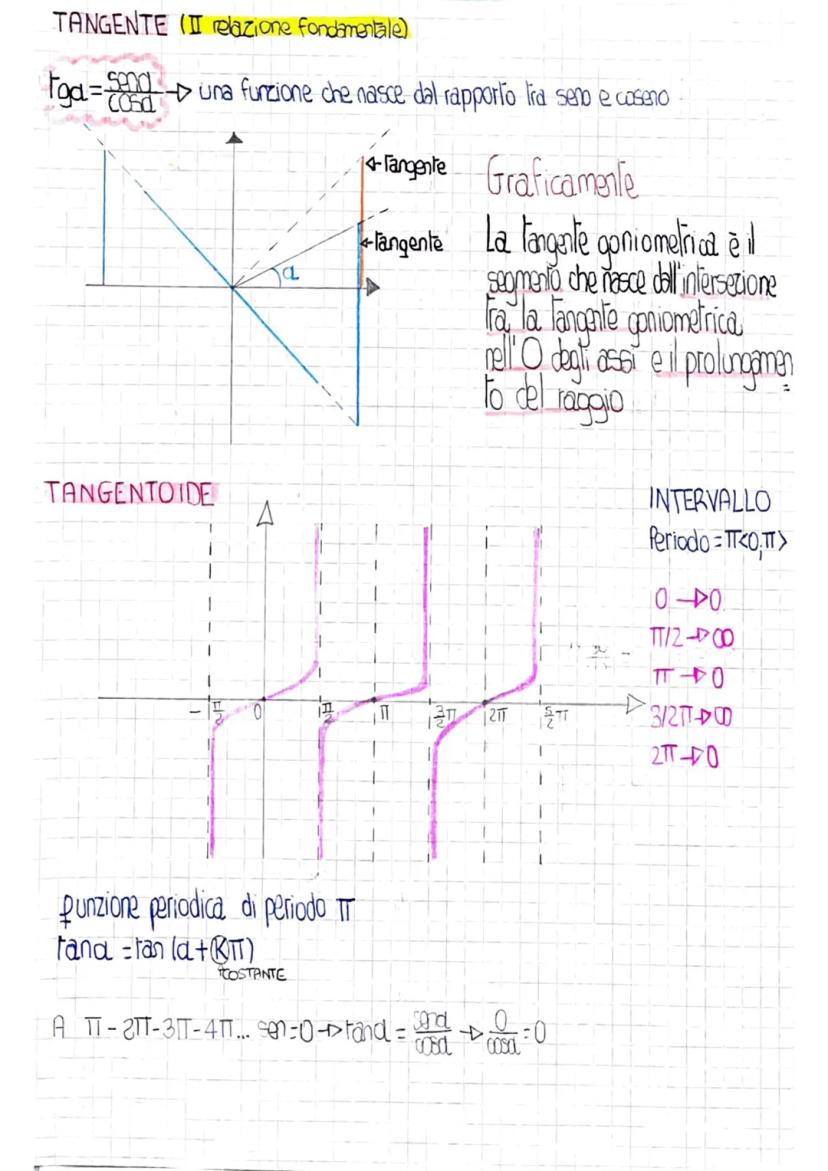
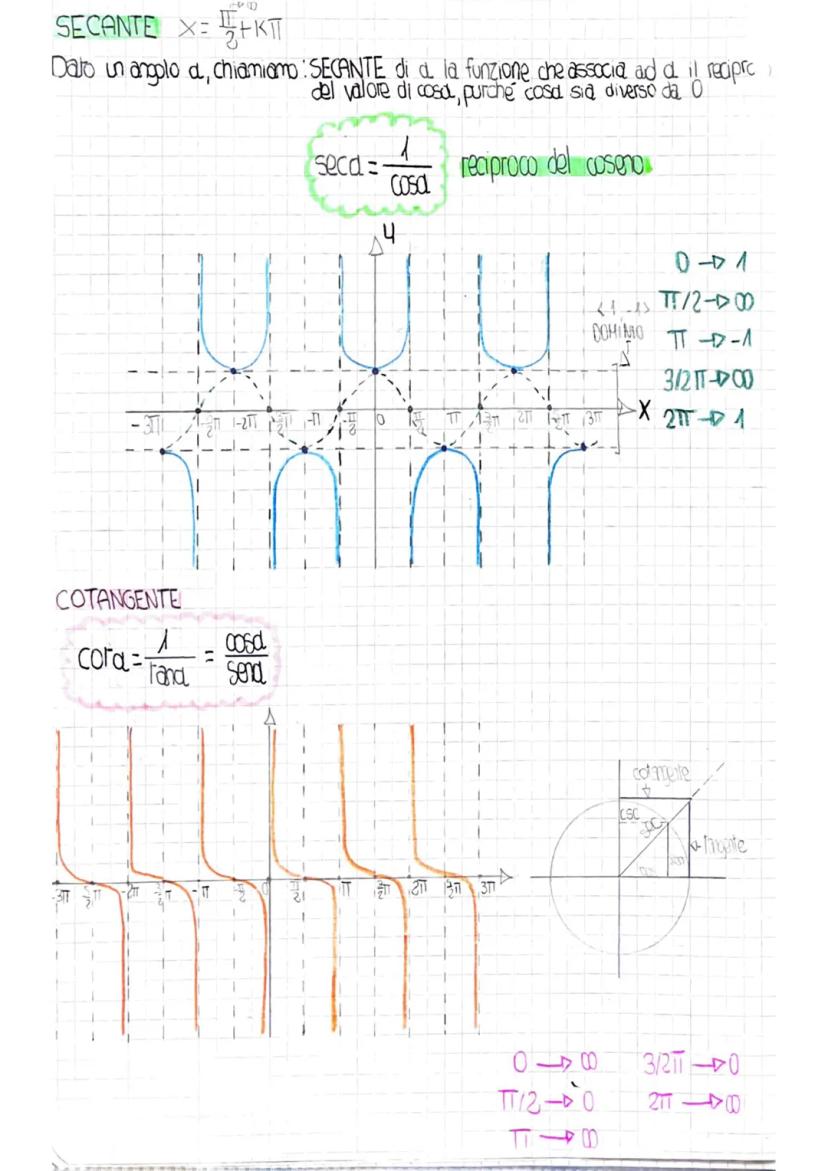
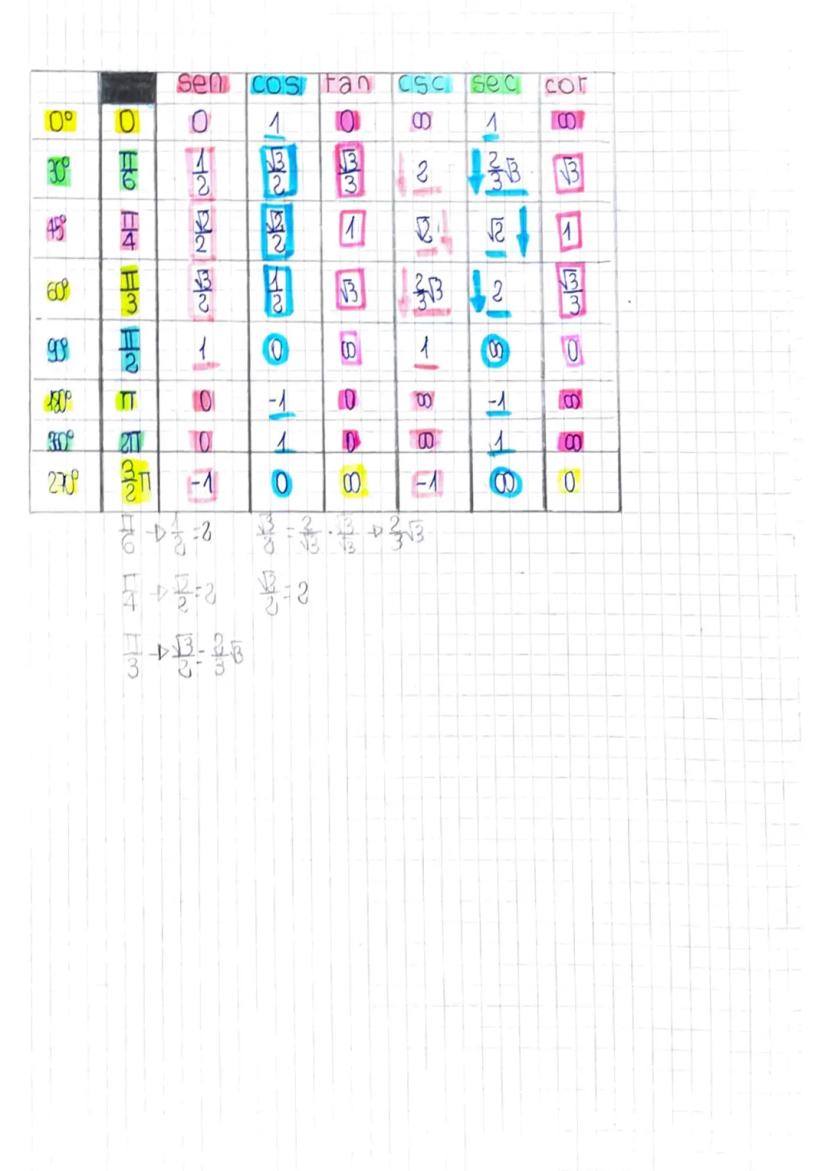
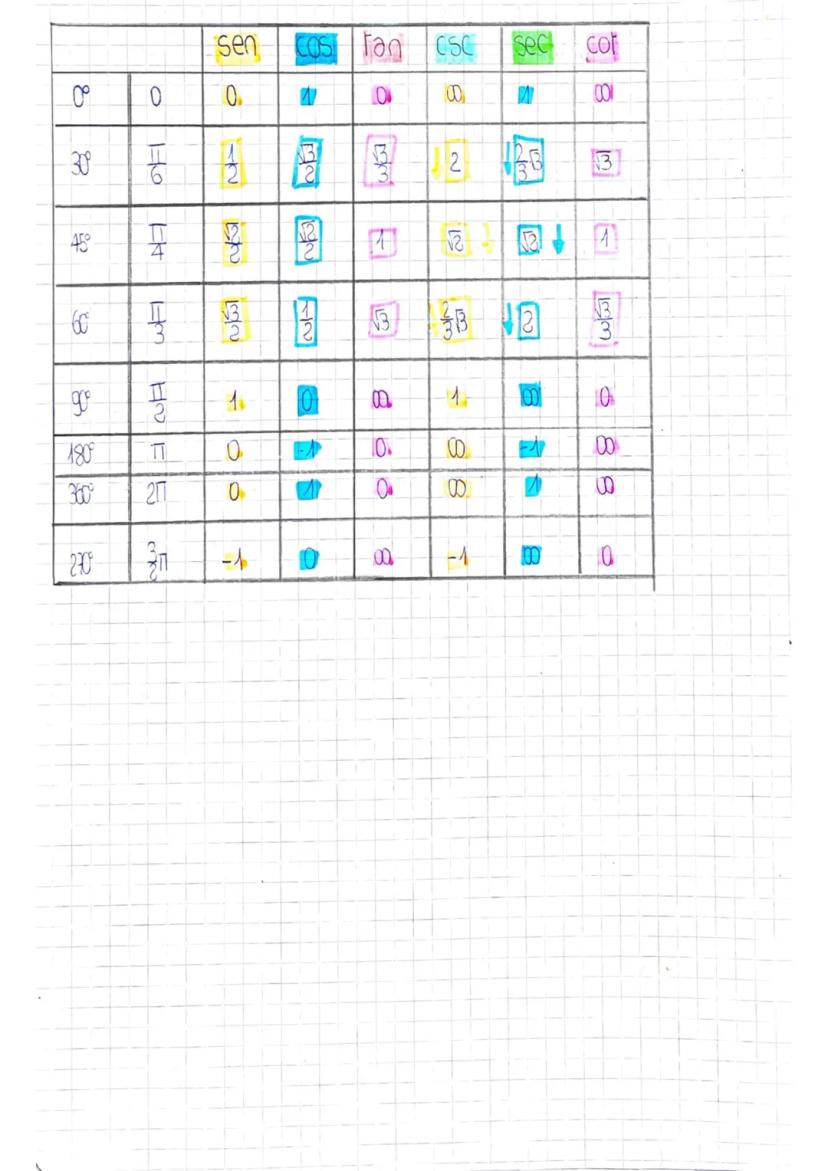
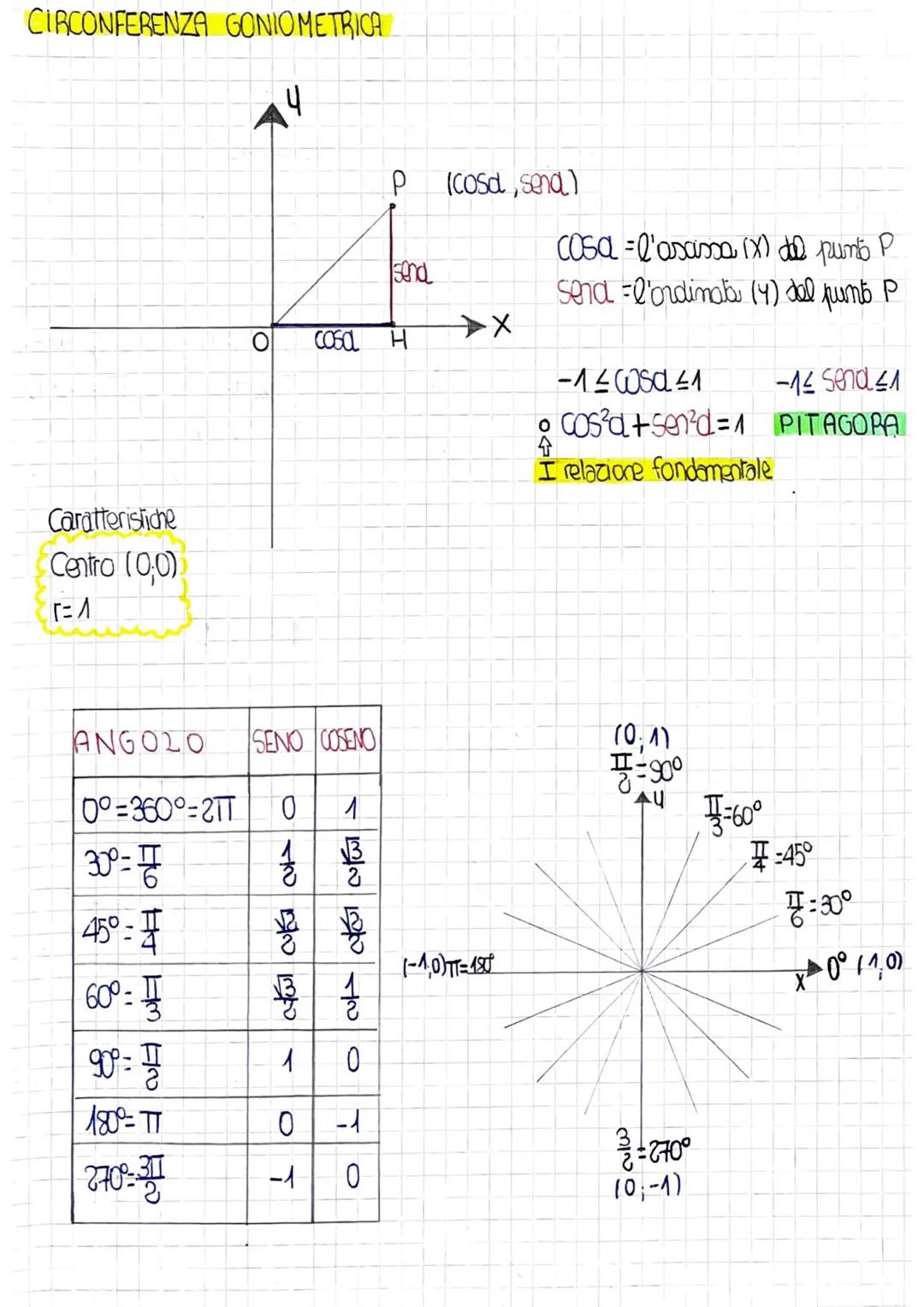
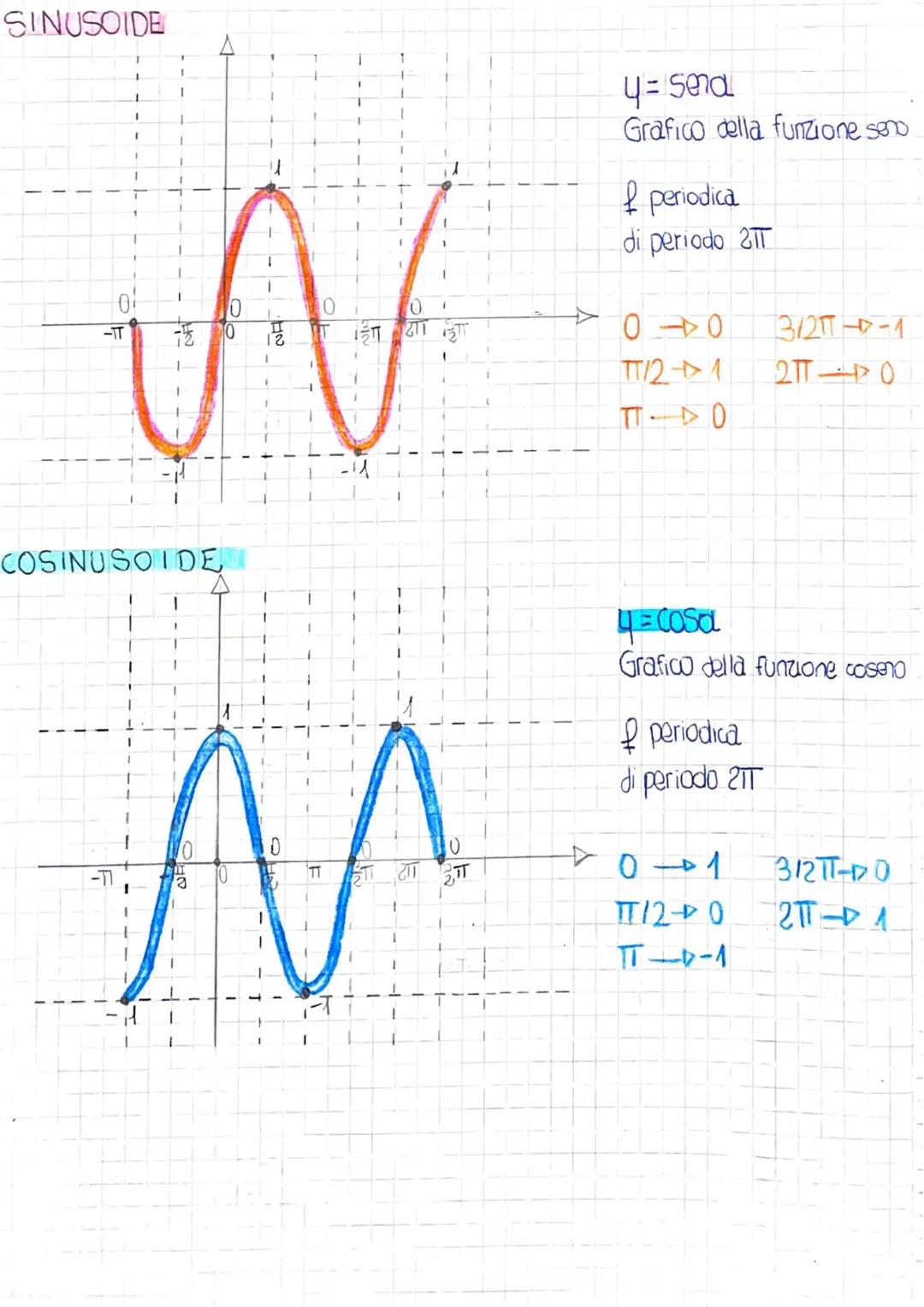
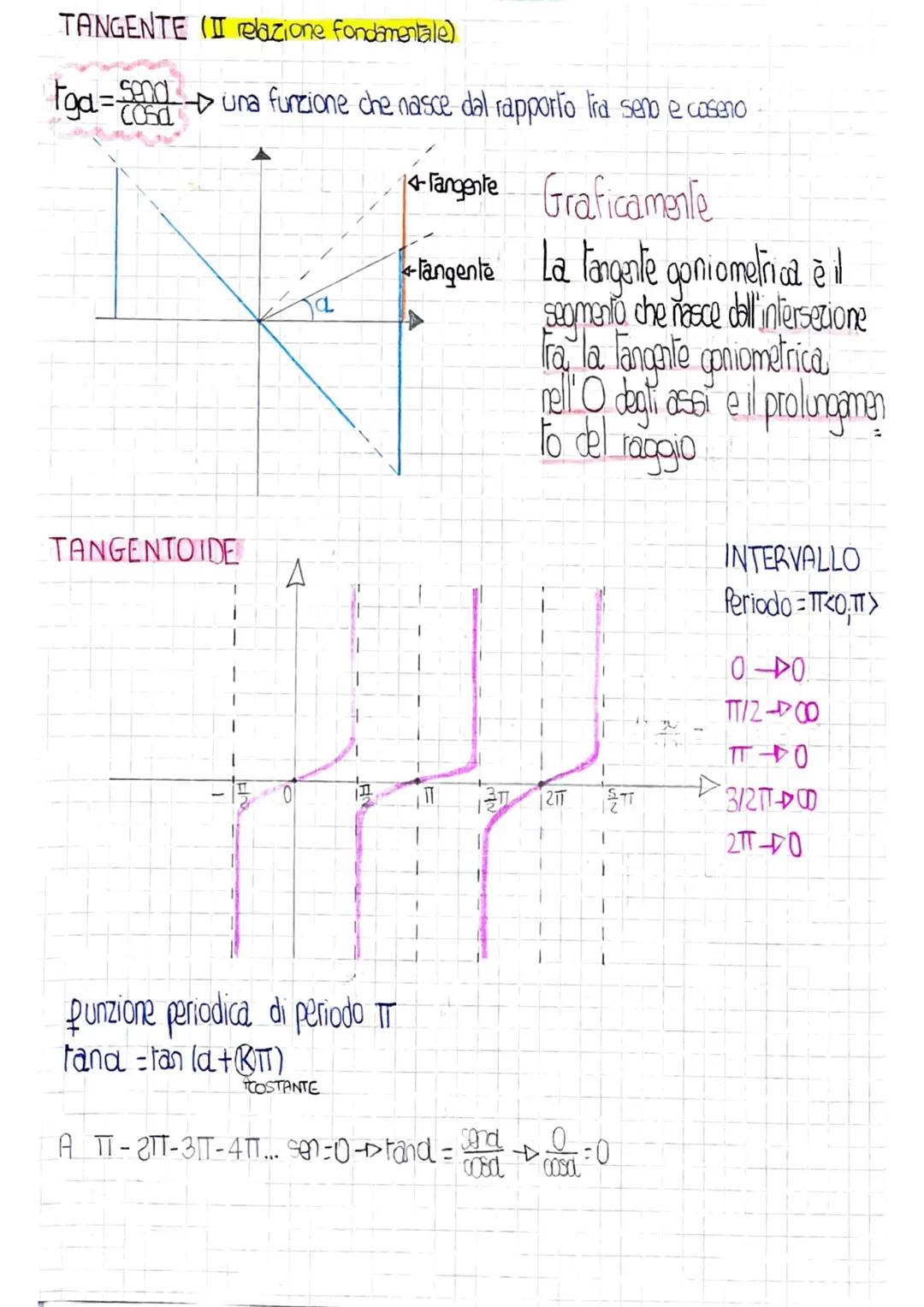
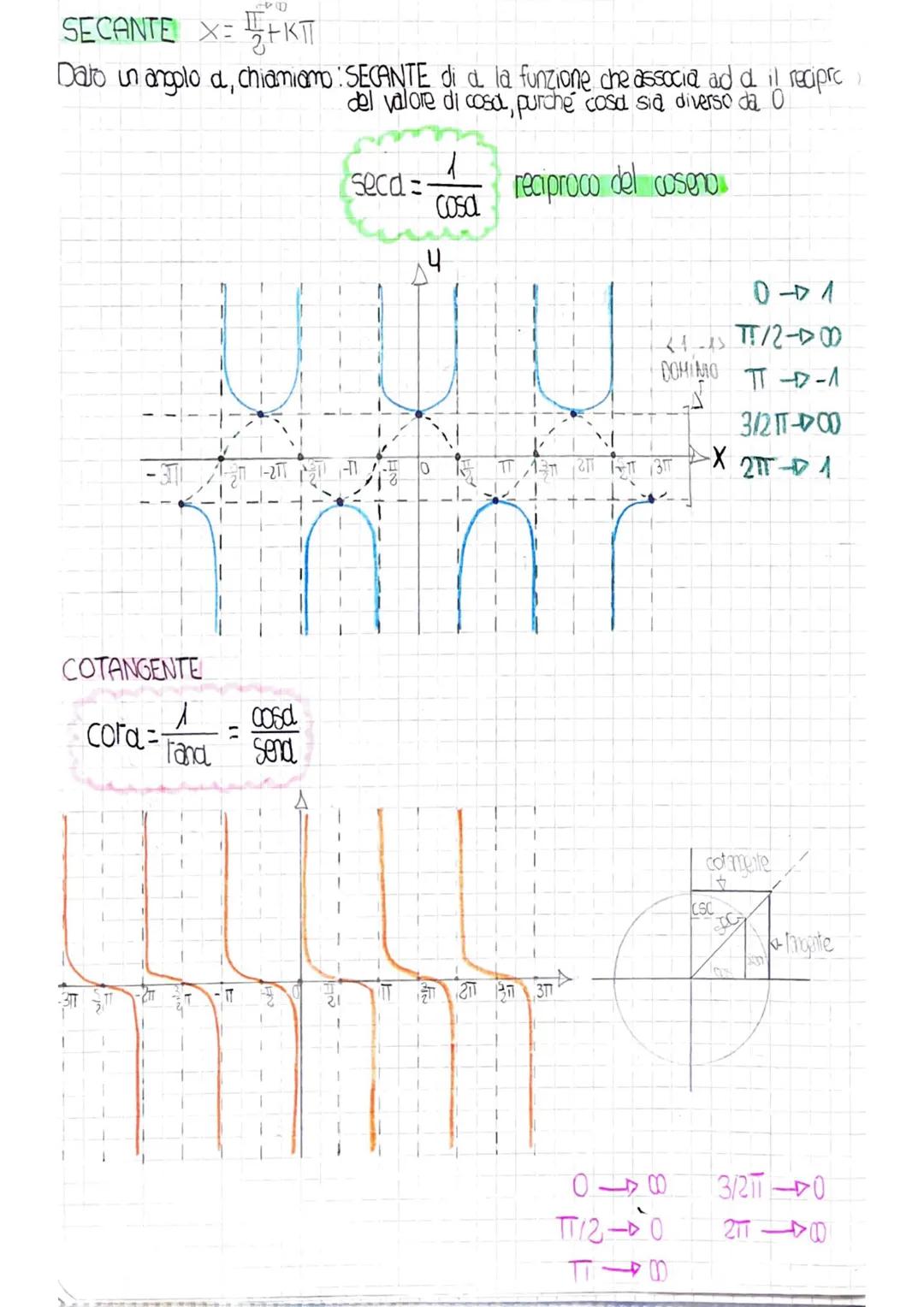
Tabella dei Valori Notevoli
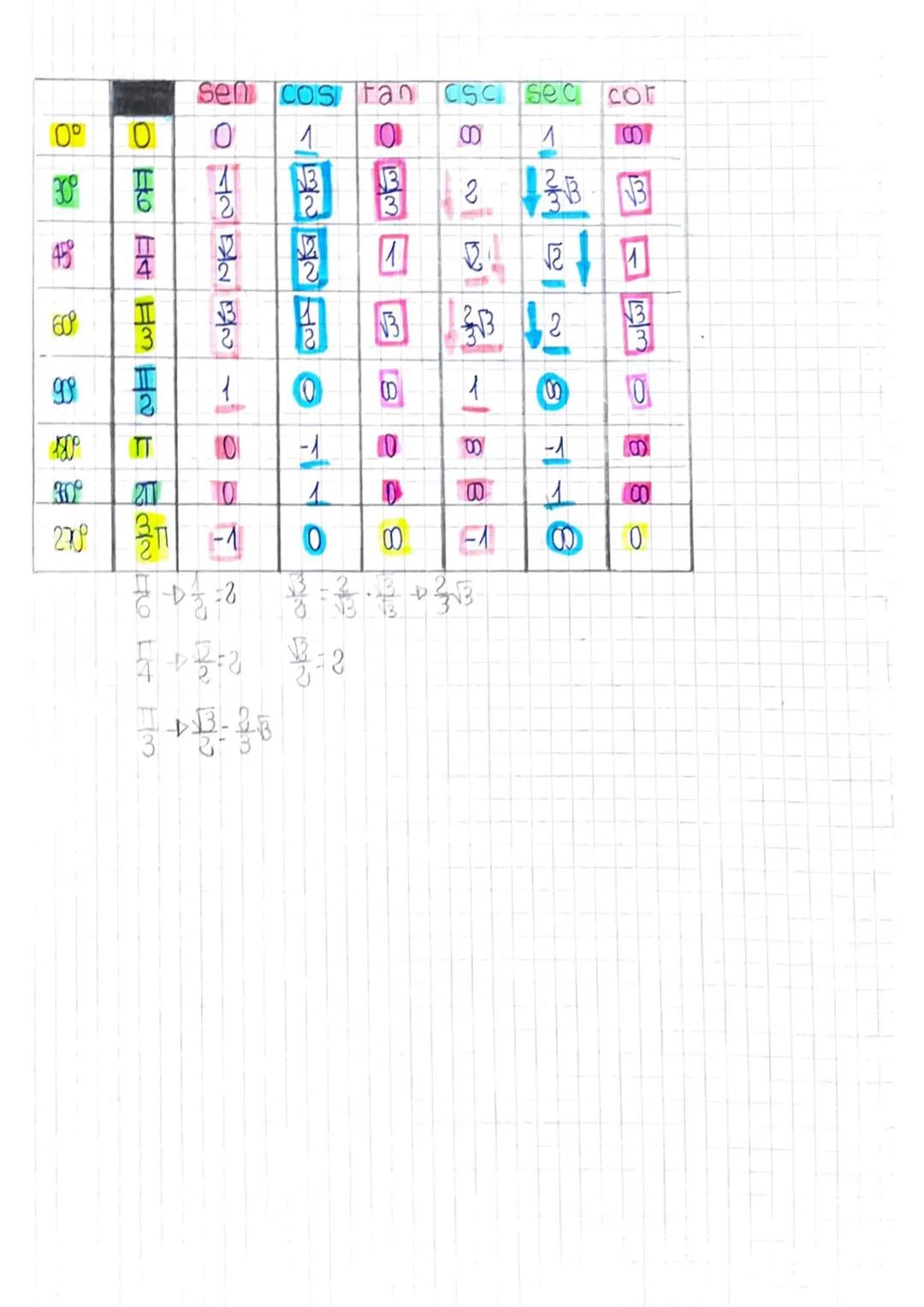
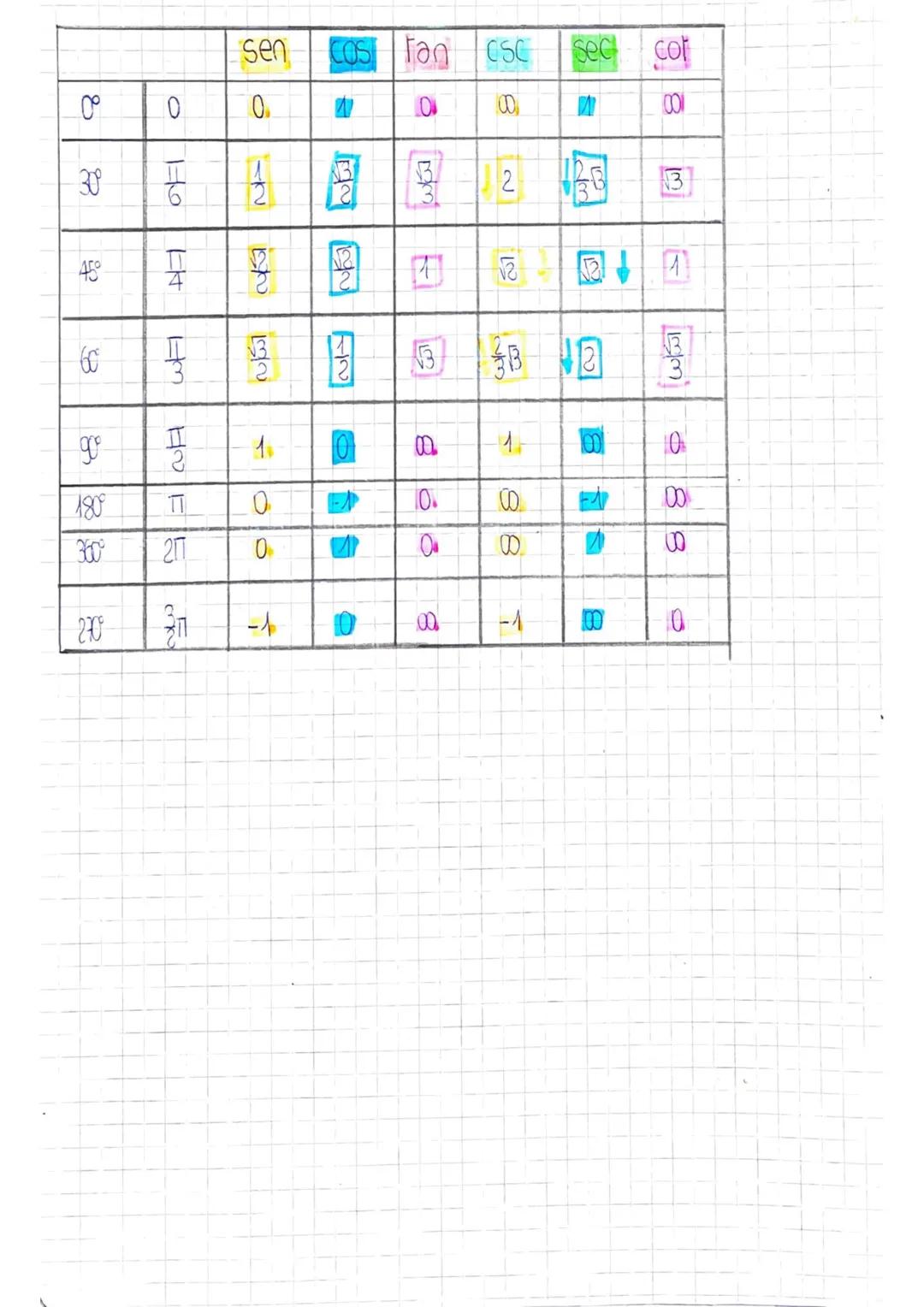
Questa tabella riassume i valori delle funzioni goniometriche per gli angoli fondamentali. È essenziale memorizzarla per risolvere rapidamente esercizi e problemi.
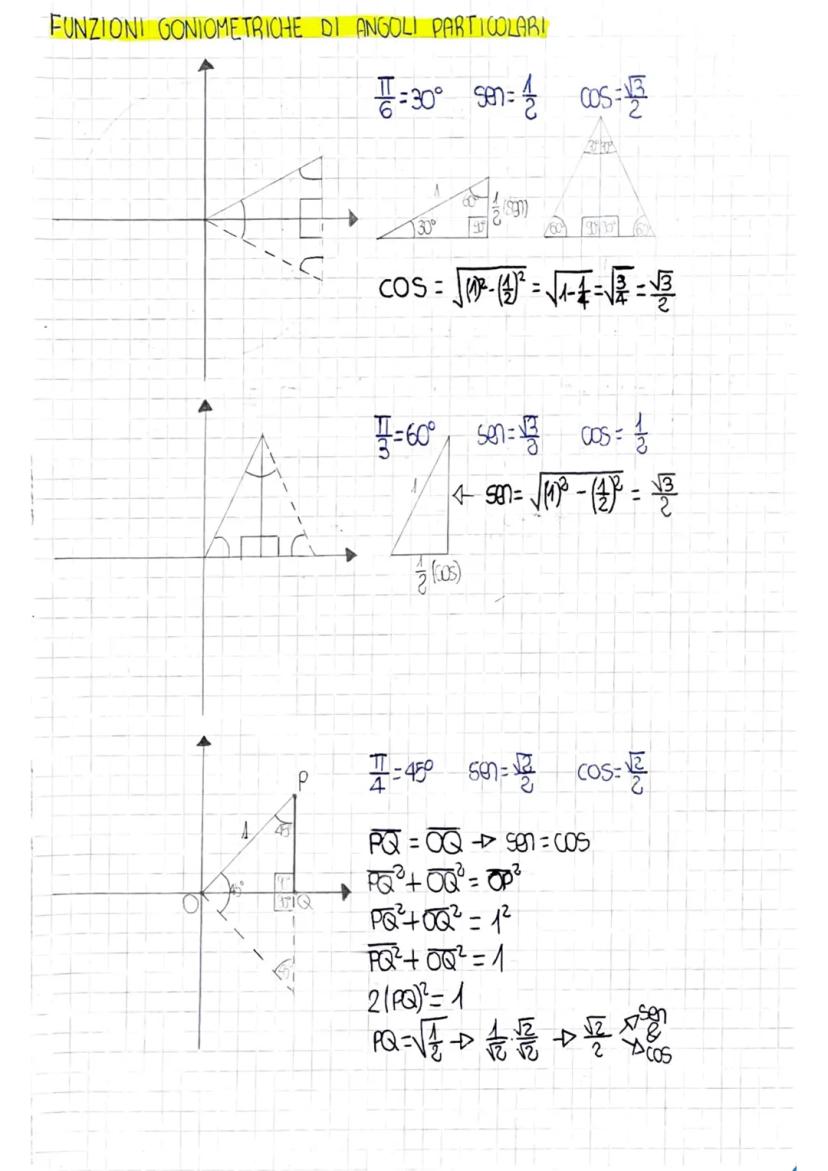
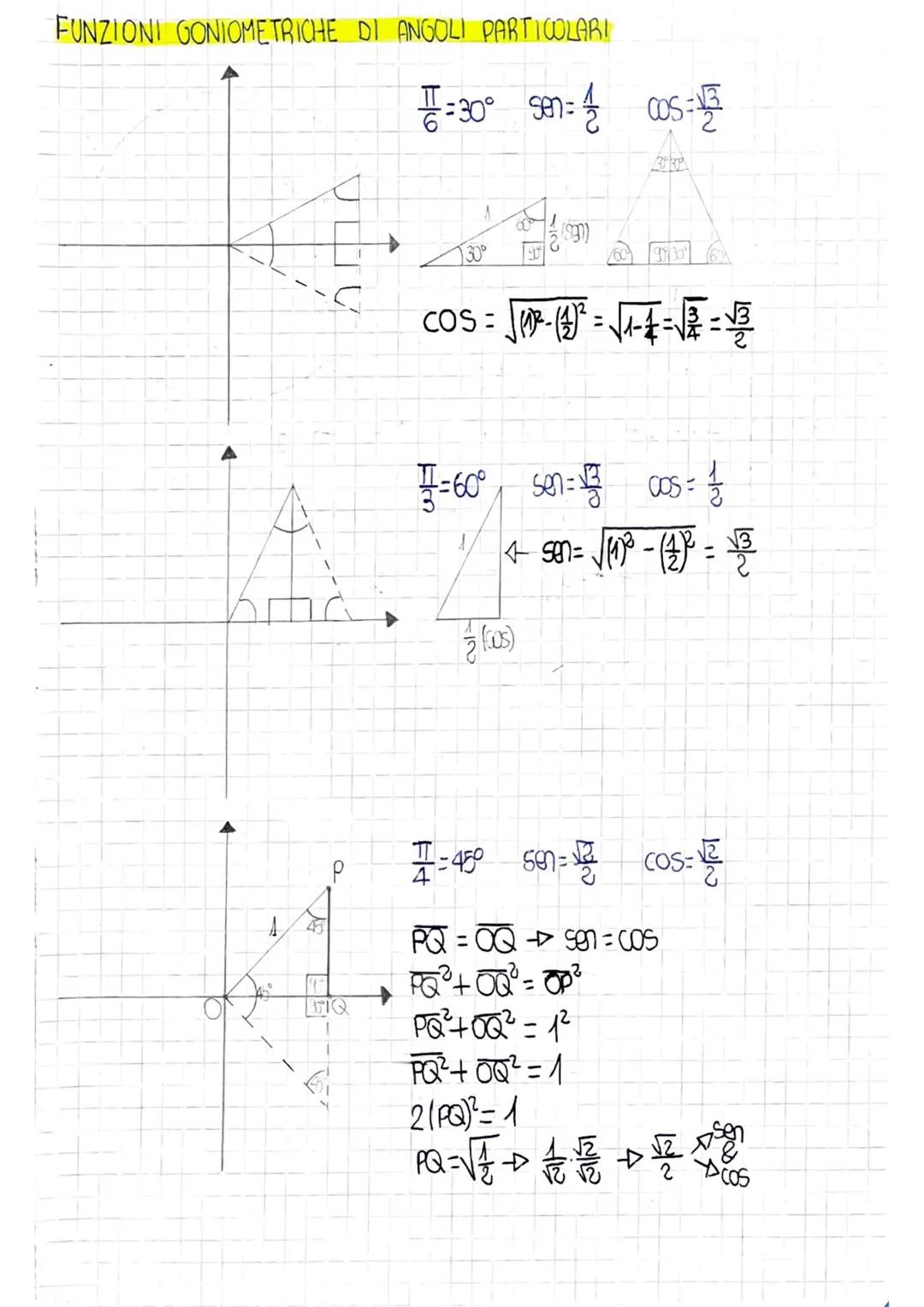
Gli angoli più importanti sono 0°, 30°, 45°, 60°, 90°, 180°, 270° e 360°. Per 30°, 45° e 60° i valori coinvolgono spesso √2, √3 e frazioni semplici.
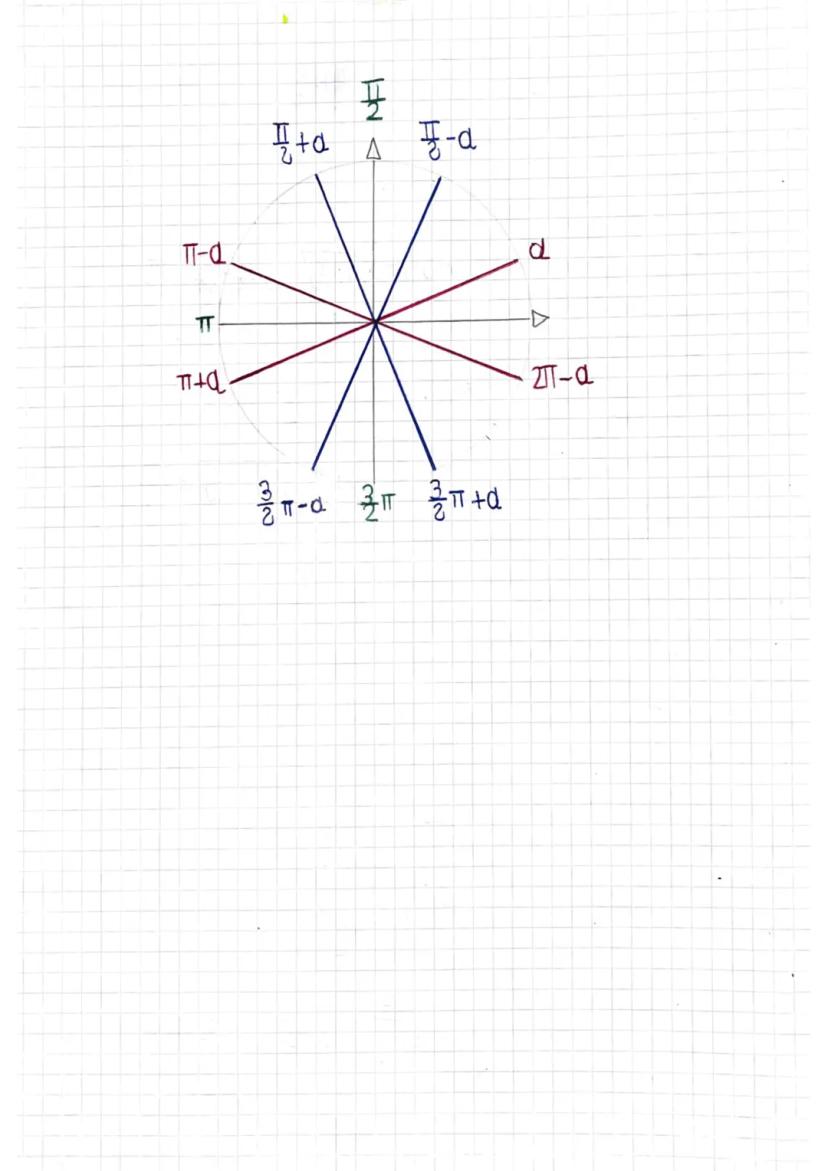
Noterai dei pattern: i valori di seno e coseno a 30° e 60° sono "scambiati", mentre a 45° sono uguali. Le funzioni reciproche (csc, sec, cot) seguono automaticamente i valori delle funzioni base.
💡 Metodo di studio: Non limitarti a memorizzare - cerca i pattern e le relazioni tra i valori!