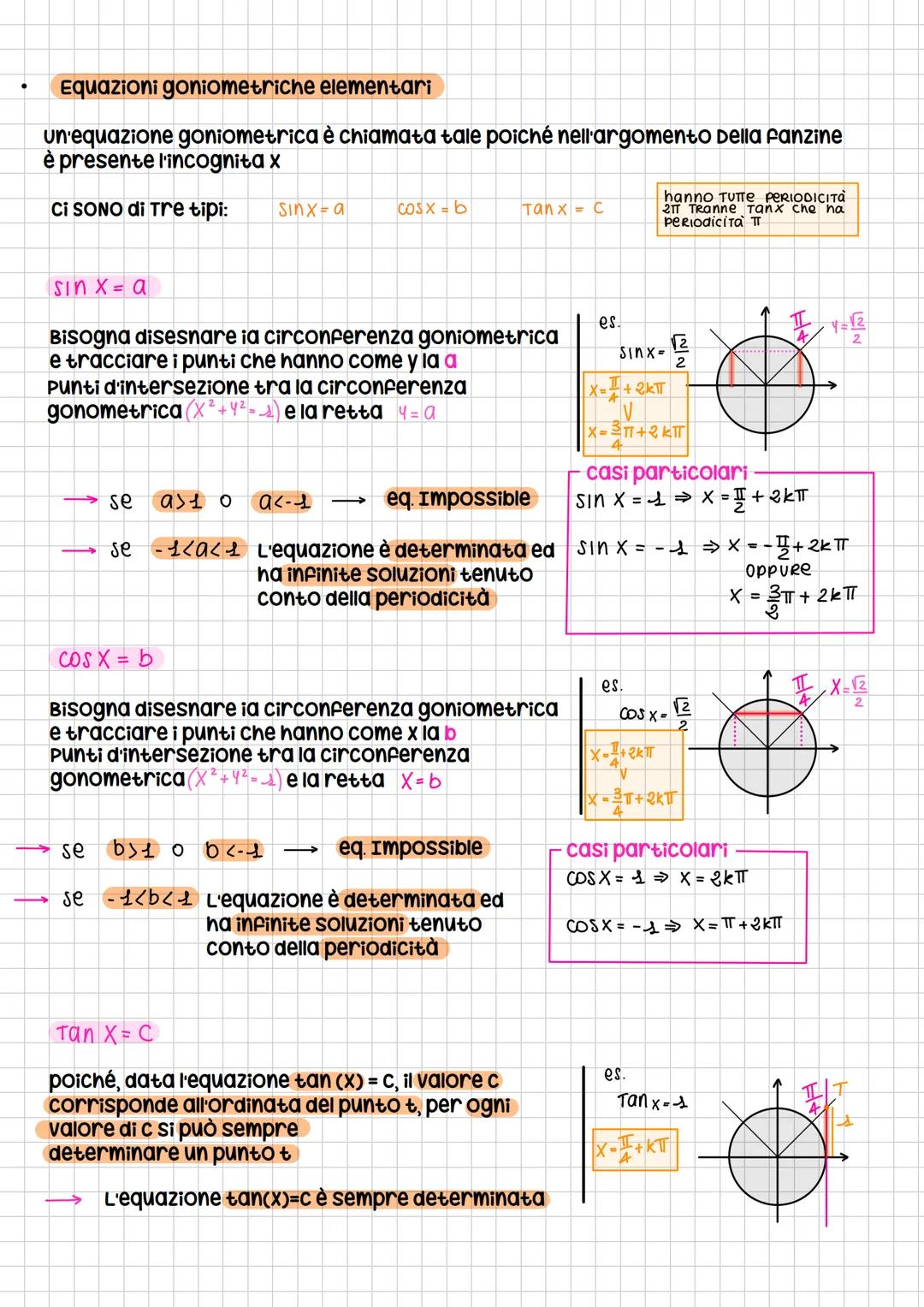
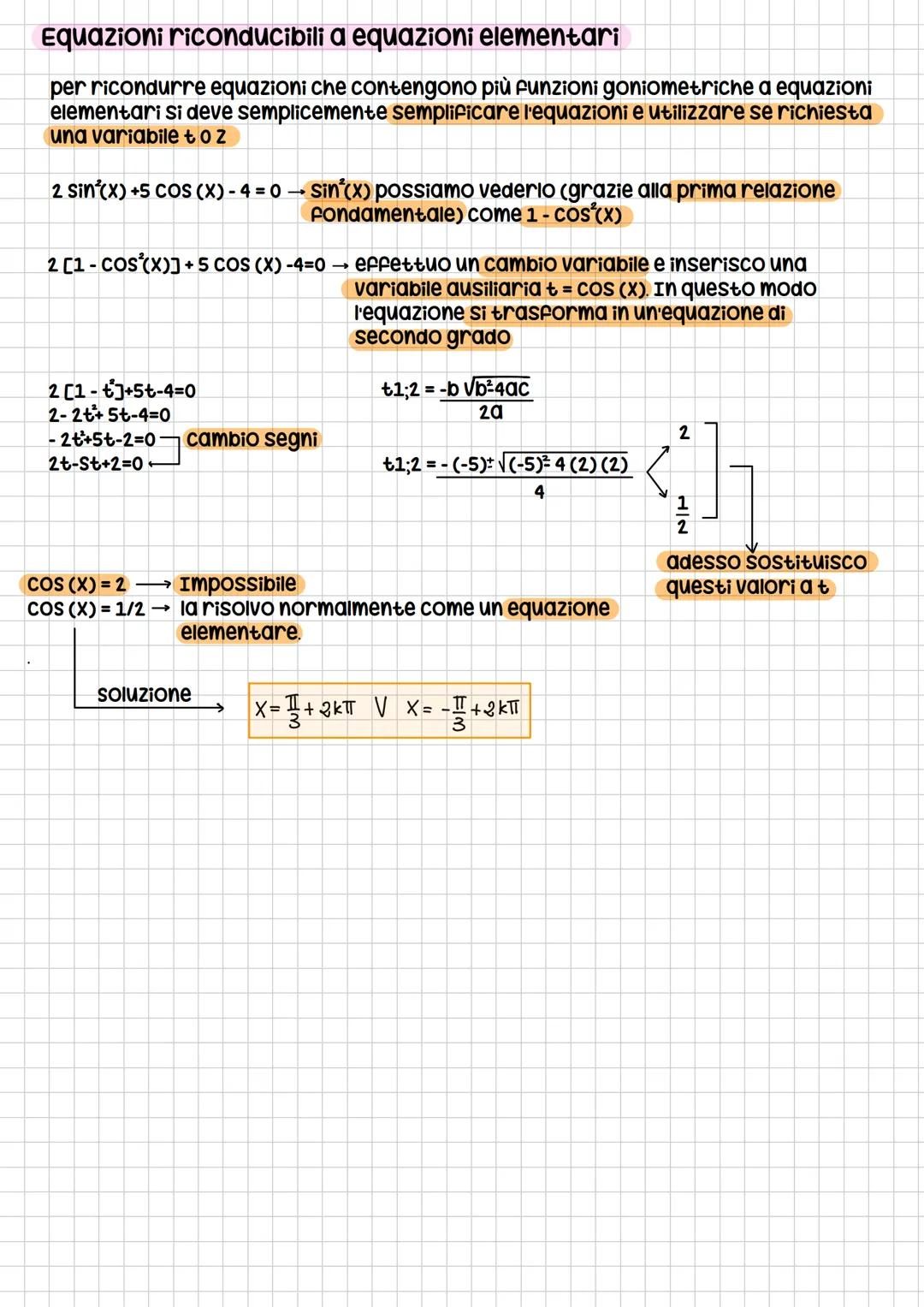
Equazioni Goniometriche Elementari
Quando vedi un'equazione goniometrica elementare, stai guardando una delle tre forme base: sin x = a, cos x = b, o tan x = c. Queste sono i mattoncini fondamentali che devi padroneggiare!
Per risolvere sin x = a, disegni la circonferenza goniometrica e tracci la retta orizzontale y = a. I punti dove si intersecano ti danno le soluzioni. Se a è maggiore di 1 o minore di -1, l'equazione è impossibile perché il seno non può uscire dall'intervallo [-1, 1].
Lo stesso principio vale per cos x = b, ma stavolta tracci una retta verticale x = b. Anche qui, se b esce dall'intervallo [-1, 1], non ci sono soluzioni.
Trucco importante: La tangente è diversa! L'equazione tan x = c ha sempre soluzioni per qualsiasi valore di c, perché la tangente può assumere tutti i valori reali.