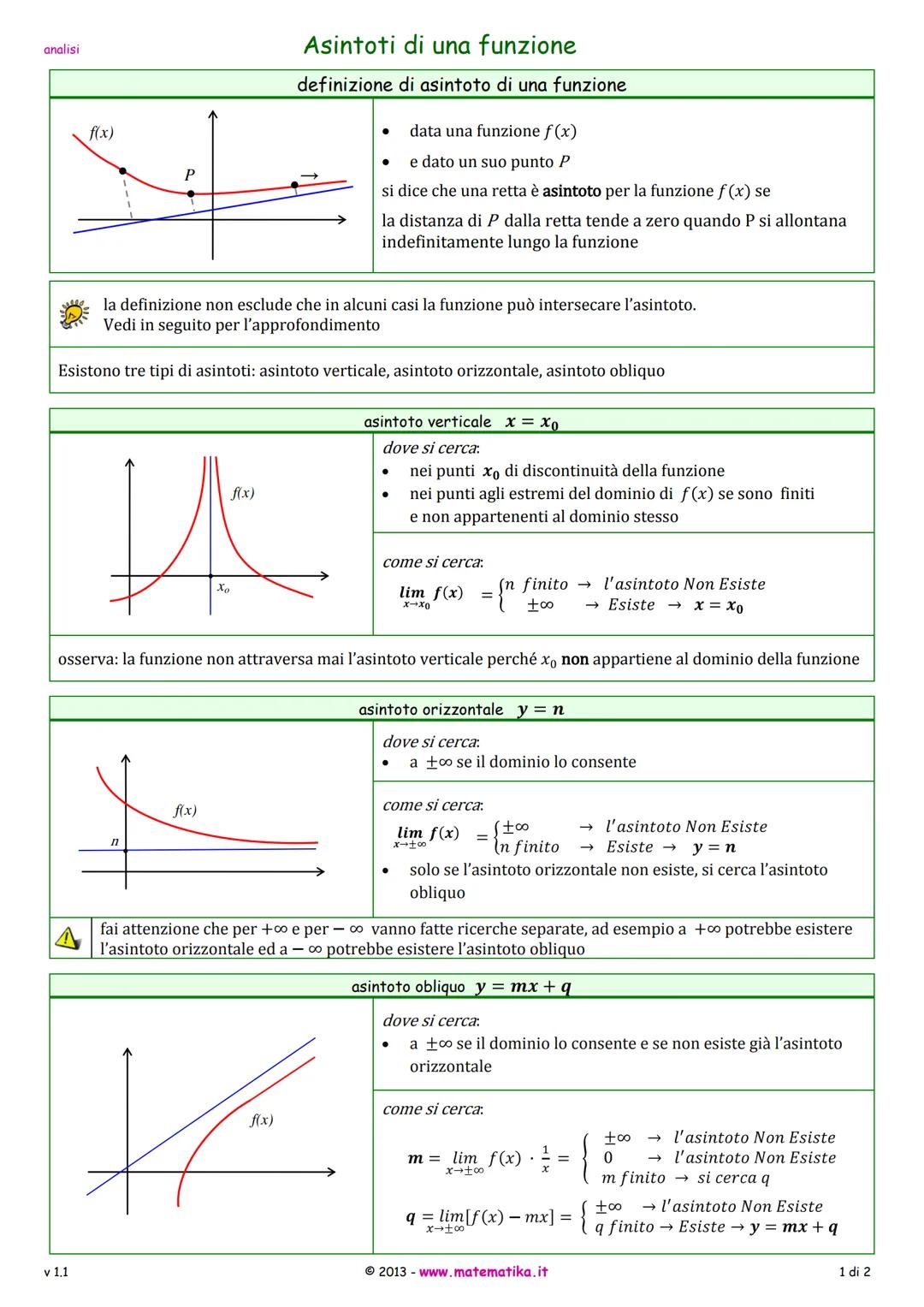
Asintoti obliqui ed esempi pratici
Se non esiste l'asintoto orizzontale, puoi cercare quello obliquo con equazione y = mx + q. Prima calcoli m = limf(x)/x per x→±∞, poi q = limf(x)−mx. Se entrambi danno valori finiti (e m ≠ 0), hai il tuo asintoto obliquo!
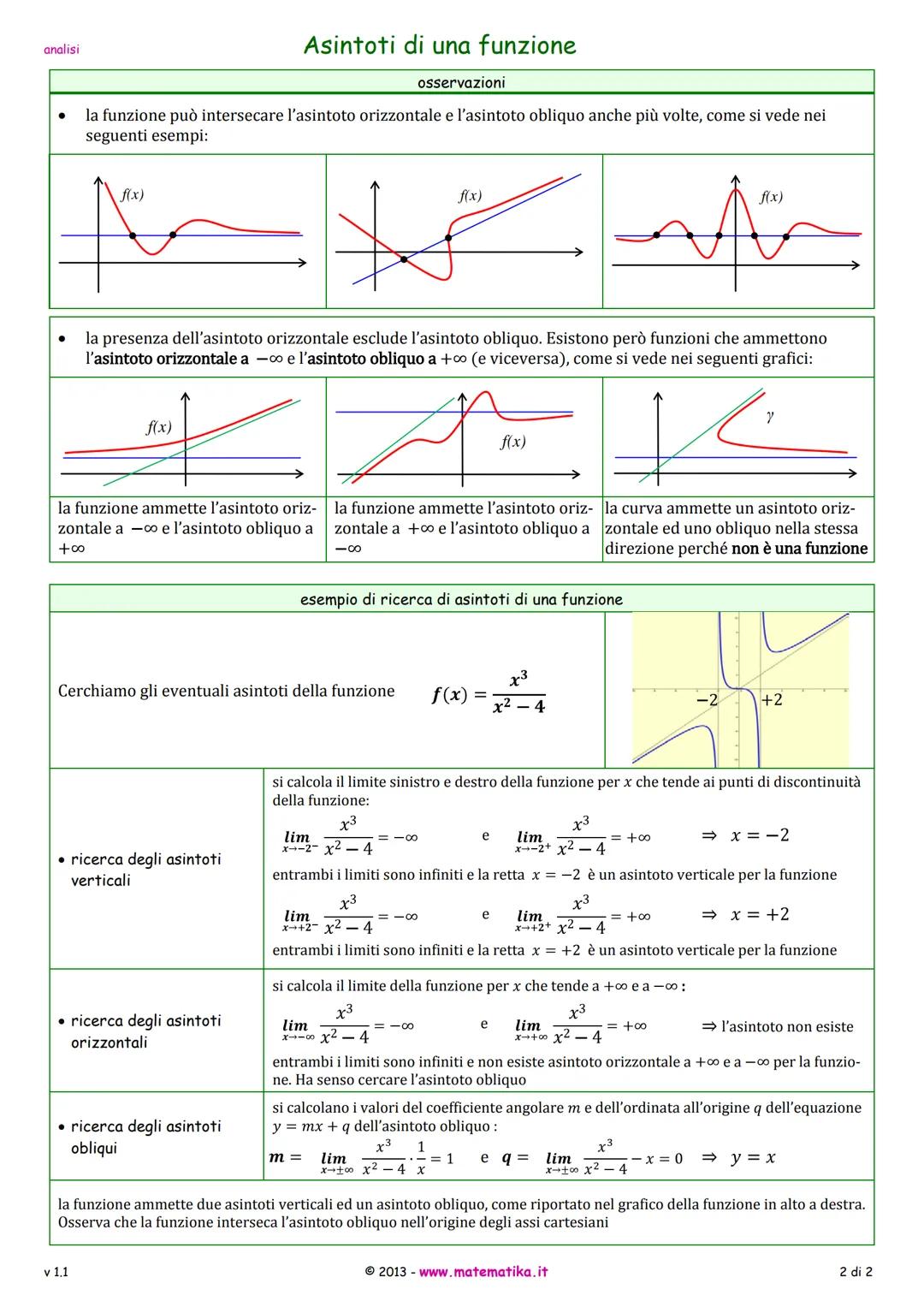
Ecco un esempio concreto con f(x) = x³/x2−4. I punti x = -2 e x = +2 danno limiti infiniti, quindi sono asintoti verticali. Per gli estremi, i limiti danno ±∞, quindi niente asintoto orizzontale.
Per l'asintoto obliquo: m = 1 e q = 0, quindi y = x è l'asintoto obliquo. Interessante notare che questa funzione attraversa il suo asintoto obliquo nell'origine!
Attenzione: Una funzione può avere l'asintoto orizzontale da una parte es.+∞ e quello obliquo dall'altra (-∞). Controlla sempre entrambe le direzioni separatamente!