Matematica

Trasformazioni di Grafici e Figure

Traslazioni

543

•

Aggiornato Mar 31, 2026

•

4 pagine

Funzioni Matematiche e le Loro Caratteristiche

Giorgia Fasola

@giorgiafasola

Le funzioni sono uno degli argomenti più importanti di matematica... Mostra di più

1 / 4

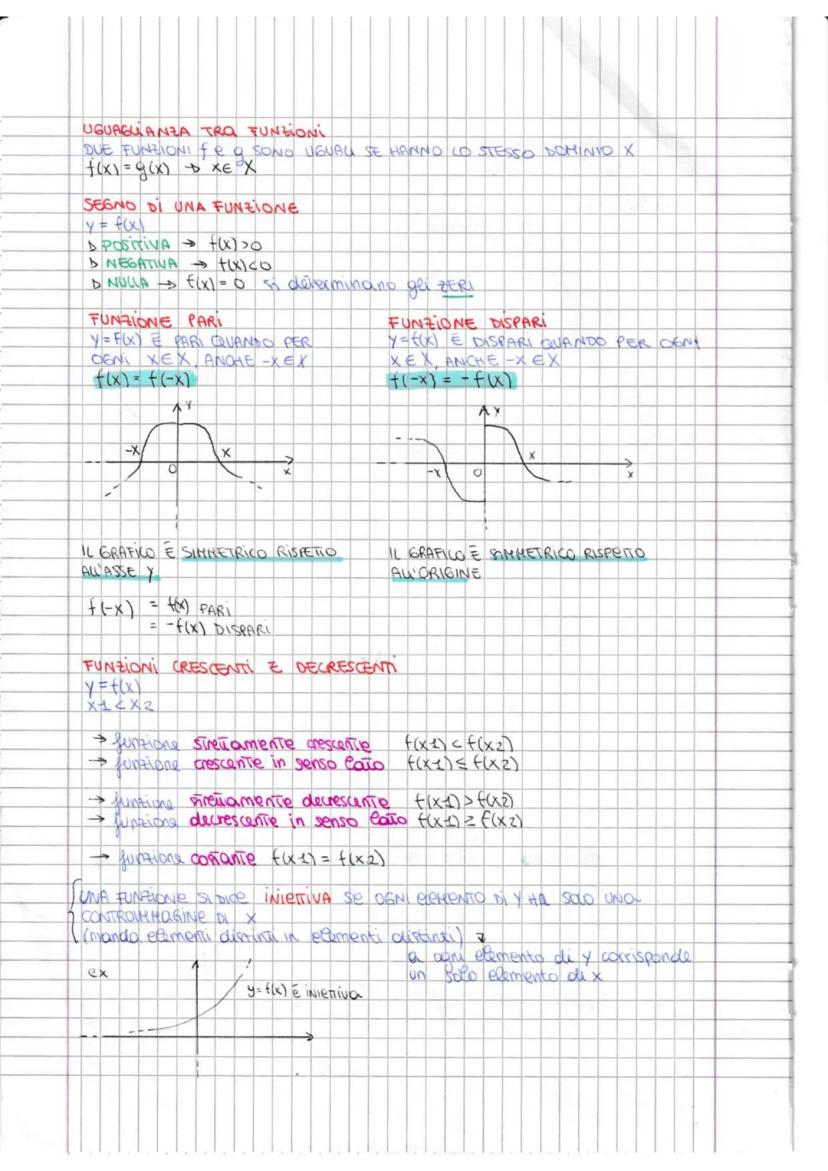
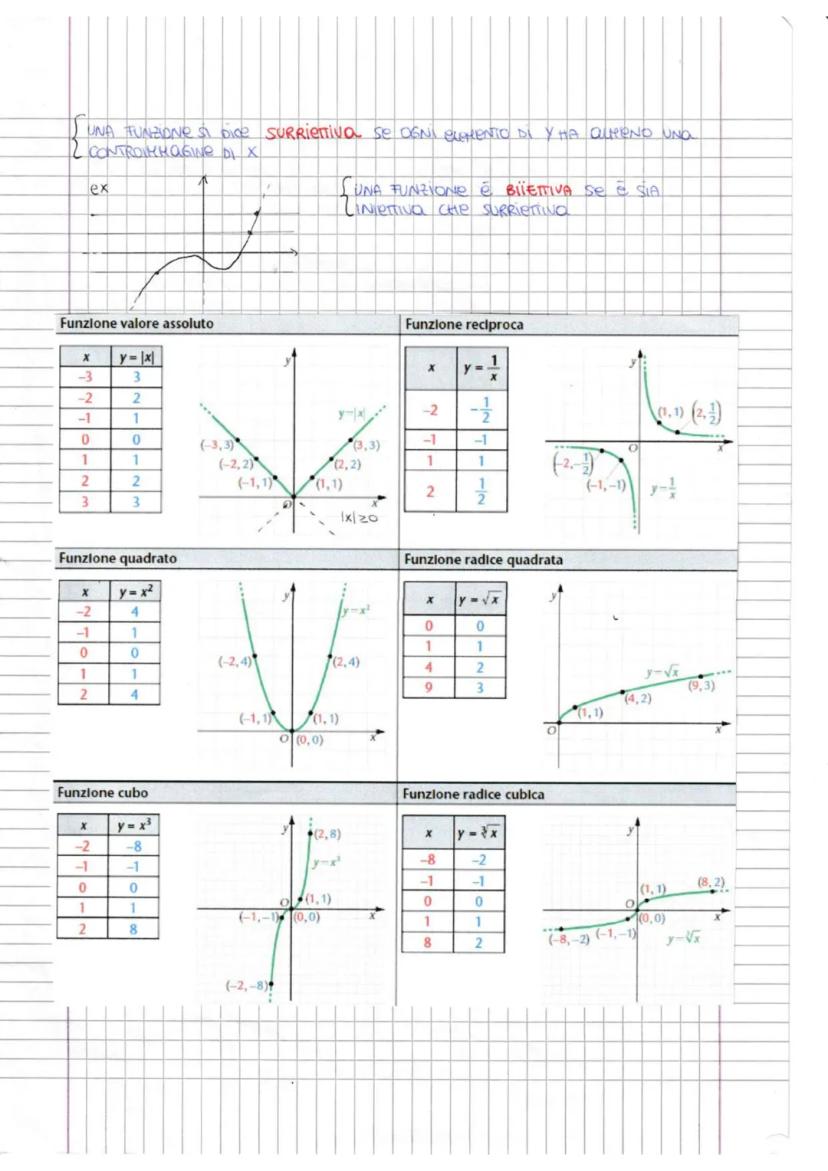
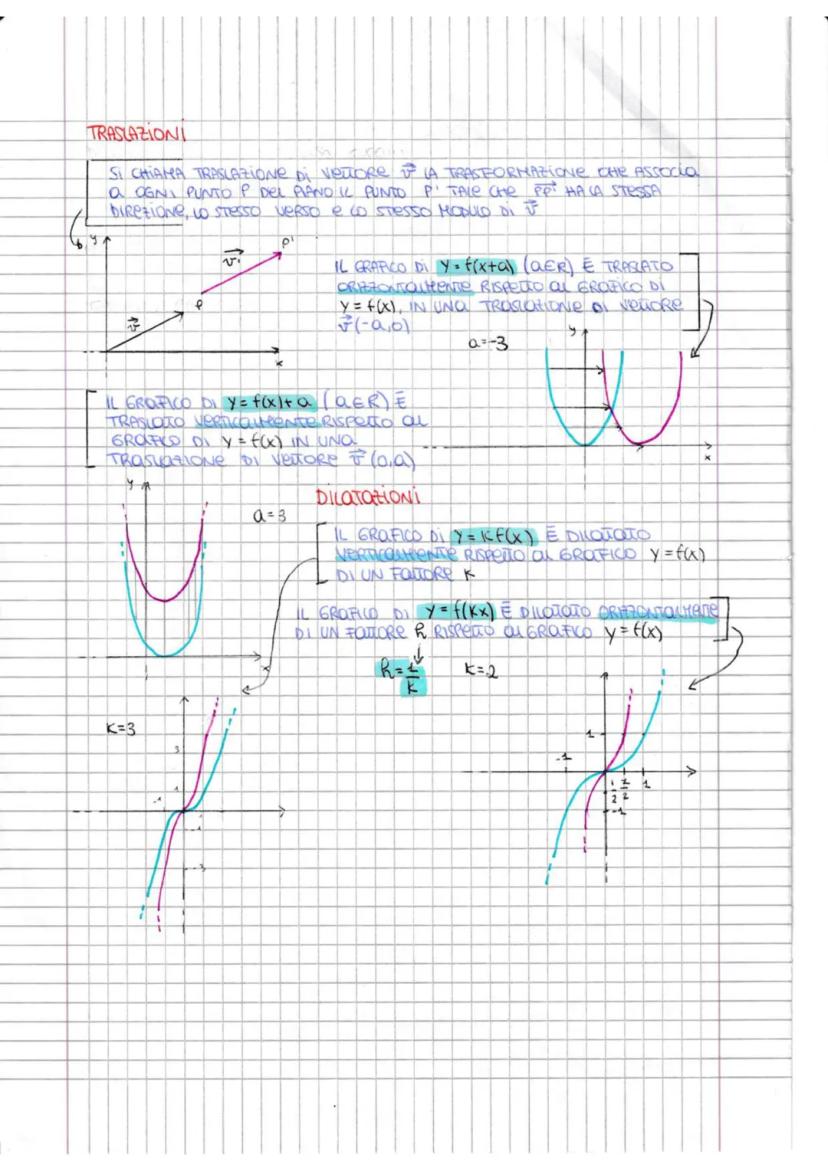
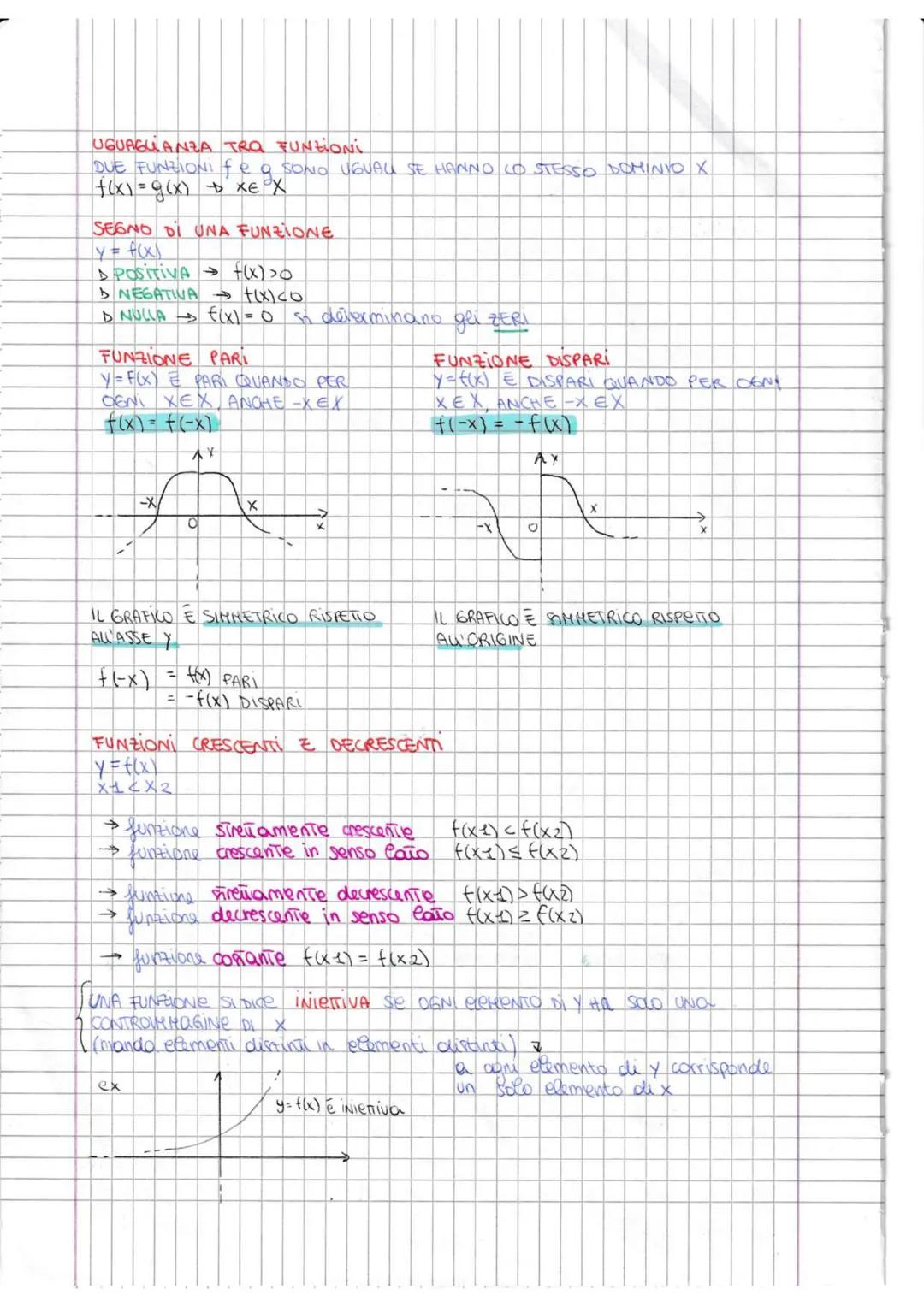
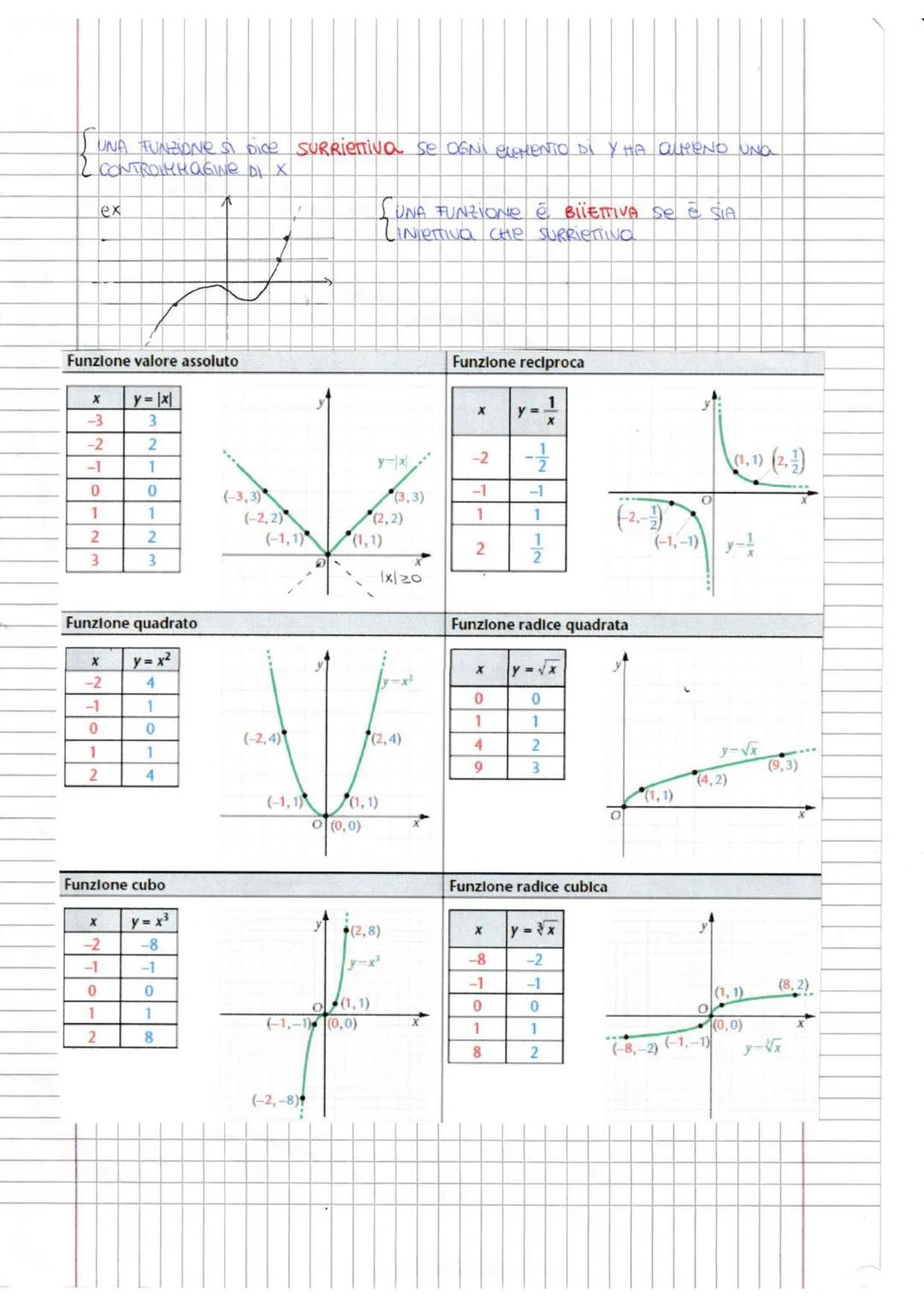
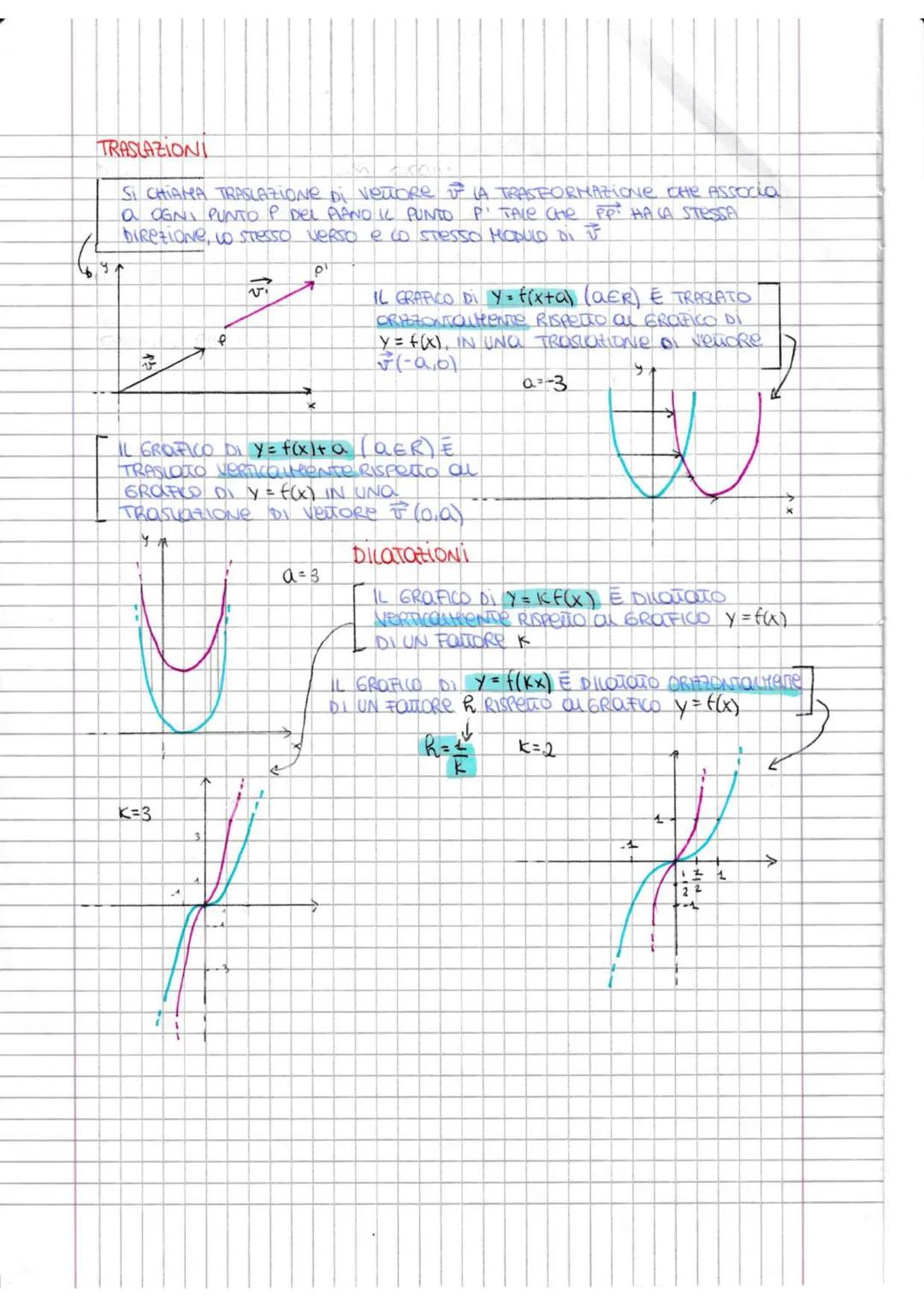
# FUNZIONI

DEFINIZIONE: SIAND X ED Y DUE INSIEMI
SI DICE FUNZIONE DA XAY UNA RELAZIONE CHE ASSOCIA
AD OGNI ELEMENTO DIX UN SOLO ELEMENTO DI

Cos'è una Funzione e Come Classificarla

Immagina una funzione come una macchina: inserisci un numero (x) e ne esce sempre uno solo (y). Più formalmente, una funzione associa ad ogni elemento di un insieme X (chiamato dominio) un solo elemento di un insieme Y (chiamato codominio).

La scritta y = f(x) è l'espressione analitica della funzione. Il dominio sono tutti i valori che x può assumere, mentre l'immagine sono i valori che effettivamente assume y.

Le funzioni si dividono in due grandi famiglie: algebriche $che usano solo operazioni come +, -, ×, ÷, radici e potenze$ e trascendenti (con esponenziali, logaritmi, funzioni trigonometriche). Le algebriche possono essere razionali o irrazionali, intere o frazionarie.

Ricorda: Per trovare il dominio di una funzione algebrica, controlla che i denominatori siano diversi da zero e i radicandi maggiori o uguali a zero!

Le funzioni principali che devi conoscere sono: lineare $y = mx + q$ , quadratica $y = ax² + bx + c$ e di proporzionalità inversa $xy = k$ . Ognuna ha il suo grafico caratteristico e le sue proprietà.

Proprietà e Caratteristiche delle Funzioni

Due funzioni sono uguali quando hanno lo stesso dominio e f(x) = g(x) per ogni valore di x. Per studiare il segno di una funzione, devi capire quando è positiva (f(x) > 0), negativa (f(x) < 0) o nulla $f(x) = 0, cioè trovare gli zeri$ .

Le funzioni pari sono simmetriche rispetto all'asse y e verificano f $-x$ = f(x). Le funzioni dispari sono simmetriche rispetto all'origine e verificano f $-x$ = -f(x). Questi concetti ti aiutano a capire la forma del grafico.

Una funzione è crescente quando al crescere di x cresce anche y, decrescente quando al crescere di x diminuisce y. Se x₁ < x₂ e f(x₁) < f(x₂), la funzione è strettamente crescente in quel tratto.

Trucco: Per riconoscere una funzione iniettiva sul grafico, nessuna retta orizzontale deve toccare la curva in più di un punto!

Una funzione è iniettiva se elementi diversi di x danno sempre elementi diversi di y. È suriettiva se ogni elemento di y ha almeno una controimmagine in x. Se è sia iniettiva che suriettiva, si chiama biettiva.

Grafici delle Funzioni Fondamentali

Conoscere i grafici delle funzioni base ti semplificherà moltissimo lo studio. La funzione valore assoluto y = |x| ha la forma di una "V" con vertice nell'origine, sempre positiva o nulla.

La funzione reciproca y = 1/x è un'iperbole con due rami nei quadranti opposti. Non passa mai per l'origine perché non è definita in x = 0.

La funzione quadrato y = x² è una parabola con vertice nell'origine che apre verso l'alto, sempre positiva tranne nell'origine. La funzione radice quadrata y = √x esiste solo per x ≥ 0 ed è crescente.

Attenzione: La funzione radice quadrata ha dominio [0, +∞), mentre quella reciproca ha dominio ℝ - {0}!

La funzione cubo y = x³ è sempre crescente e passa per l'origine, mentre la funzione radice cubica y = ∛x è l'inversa del cubo e ha dominio su tutti i reali. Memorizza bene questi grafici perché li userai per costruire funzioni più complesse!

Trasformazioni Geometriche dei Grafici

Le traslazioni ti permettono di spostare il grafico di una funzione senza cambiarne la forma. Se hai y = f $x + a$ , il grafico si sposta orizzontalmente di -a unità. Se hai y = f(x) + a, si sposta verticalmente di +a unità.

Attenzione al segno: y = f $x + 3$ sposta il grafico a sinistra di 3 unità, non a destra! Questo perché devi pensare a cosa succede al valore di x per ottenere lo stesso risultato.

Le dilatazioni cambiano le proporzioni del grafico. Con y = kf(x) dilati verticalmente di un fattore k: se k > 1 il grafico si "allunga" verso l'alto, se 0 < k < 1 si "schiaccia".

Formula magica: Per y = f(kx), il fattore di dilatazione orizzontale è R = 1/k. Se k = 2, il grafico si restringe della metà!

Con y = f(kx) dilati orizzontalmente: se k > 1 il grafico si restringe, se 0 < k < 1 si allarga. Queste trasformazioni sono fondamentali per costruire grafici complessi partendo da quelli elementari.

Pensavamo che non l'avreste mai chiesto....

Che cos'è l'assistente AI di Knowunity?

Il nostro assistente AI è costruito specificamente per le esigenze degli studenti. Sulla base dei milioni di contenuti presenti sulla piattaforma, possiamo fornire agli studenti risposte davvero significative e pertinenti. Ma non si tratta solo di risposte, l'assistente è in grado di guidare gli studenti attraverso le loro sfide quotidiane di studio, con piani di studio personalizzati, quiz o contenuti nella chat e una personalizzazione al 100% basata sulle competenze e sugli sviluppi degli studenti.

Dove posso scaricare l'applicazione Knowunity?

È possibile scaricare l'applicazione dal Google Play Store e dall'Apple App Store.

Knowunity è davvero gratuita?

Sì, hai accesso completamente gratuito a tutti i contenuti nell'app e puoi chattare o seguire i Creatori in qualsiasi momento. Sbloccherai nuove funzioni crescendo il tuo numero di follower. Inoltre, offriamo Knowunity Premium, che consente di studiare senza alcun limite!!

Contenuti simili

Funzioni

319

LE FUNZIONI

2122

109

Esponenziali schema riassuntivo

1891

Di più

Contenuti più popolari: Traslazioni

Dominio e traslazioni

Schema dei domini e delle trslazioni

Funzioni Matematiche e le Loro Caratteristiche

Cos'è una Funzione e Come Classificarla

Proprietà e Caratteristiche delle Funzioni

Grafici delle Funzioni Fondamentali

Trasformazioni Geometriche dei Grafici

Pensavamo che non l'avreste mai chiesto....

Che cos'è l'assistente AI di Knowunity?

Dove posso scaricare l'applicazione Knowunity?

Knowunity è davvero gratuita?

Contenuti simili

Funzioni

LE FUNZIONI

Esponenziali schema riassuntivo

Contenuti più popolari: Traslazioni

Dominio e traslazioni

Contenuti più popolari di Matematica

I RADICALI

Monomi

Derivate

Monomi e operazioni tra monomi

Operazioni e prodotti notevoli

Derivate

Funzioni

equazioni di secondo grado procedura e spiegazioni

I Radicali

Contenuti più popolari

Teoria patente b

PATENTE

Riassunto patente B

I promessi sposi

Teoria patente di guida B: Segnali stradali

promessi sposi (capitoli 1-18)

I promessi sposi

SEGNALETICA STRADALE

PATENTE B

Non c'è niente di adatto? Esplorare altre aree tematiche.

Recensioni dei nostri utenti. Ci adorano - e anche tu, vedrai .

4.6/5

4.7/5

Funzioni Matematiche e le Loro Caratteristiche

Iscriviti per mostrare il contenutoÈ gratis!

Cos'è una Funzione e Come Classificarla

Iscriviti per mostrare il contenutoÈ gratis!

Proprietà e Caratteristiche delle Funzioni

Iscriviti per mostrare il contenutoÈ gratis!

Grafici delle Funzioni Fondamentali

Iscriviti per mostrare il contenutoÈ gratis!

Trasformazioni Geometriche dei Grafici

Pensavamo che non l'avreste mai chiesto....

Che cos'è l'assistente AI di Knowunity?

Dove posso scaricare l'applicazione Knowunity?

Knowunity è davvero gratuita?

Contenuti simili

Funzioni

LE FUNZIONI

Esponenziali schema riassuntivo

Piano cartesiano e retta

GRAFICI DELLE FUNZIONI E TRASFORMAZIONI GEOMETRICHE

Funzioni Matematiche

Contenuti simili

Funzioni

LE FUNZIONI

Esponenziali schema riassuntivo

Contenuti più popolari: Traslazioni

Dominio e traslazioni

Contenuti più popolari di Matematica

I RADICALI

Monomi

Derivate

Monomi e operazioni tra monomi

Operazioni e prodotti notevoli

Derivate

Funzioni

equazioni di secondo grado procedura e spiegazioni

I Radicali

Contenuti più popolari

Teoria patente b

PATENTE

Riassunto patente B

I promessi sposi