Angoli Associati: Le Simmetrie che Semplificano
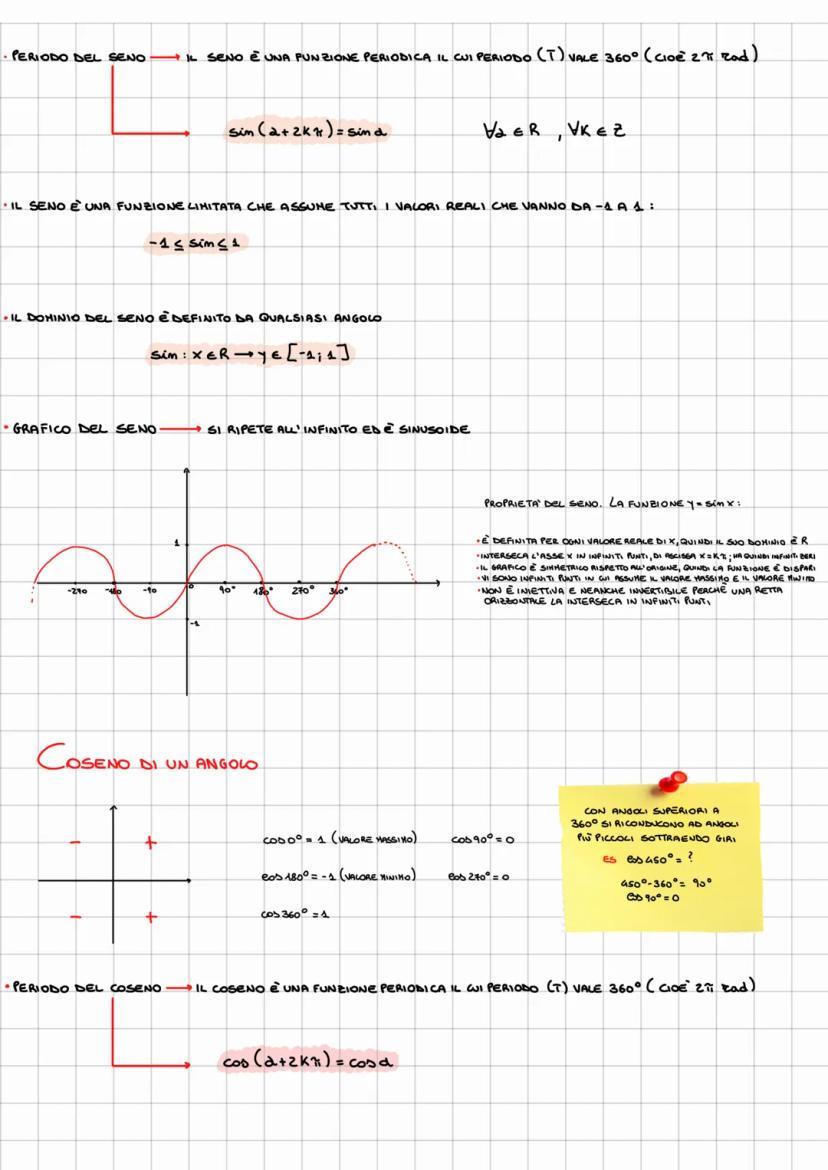
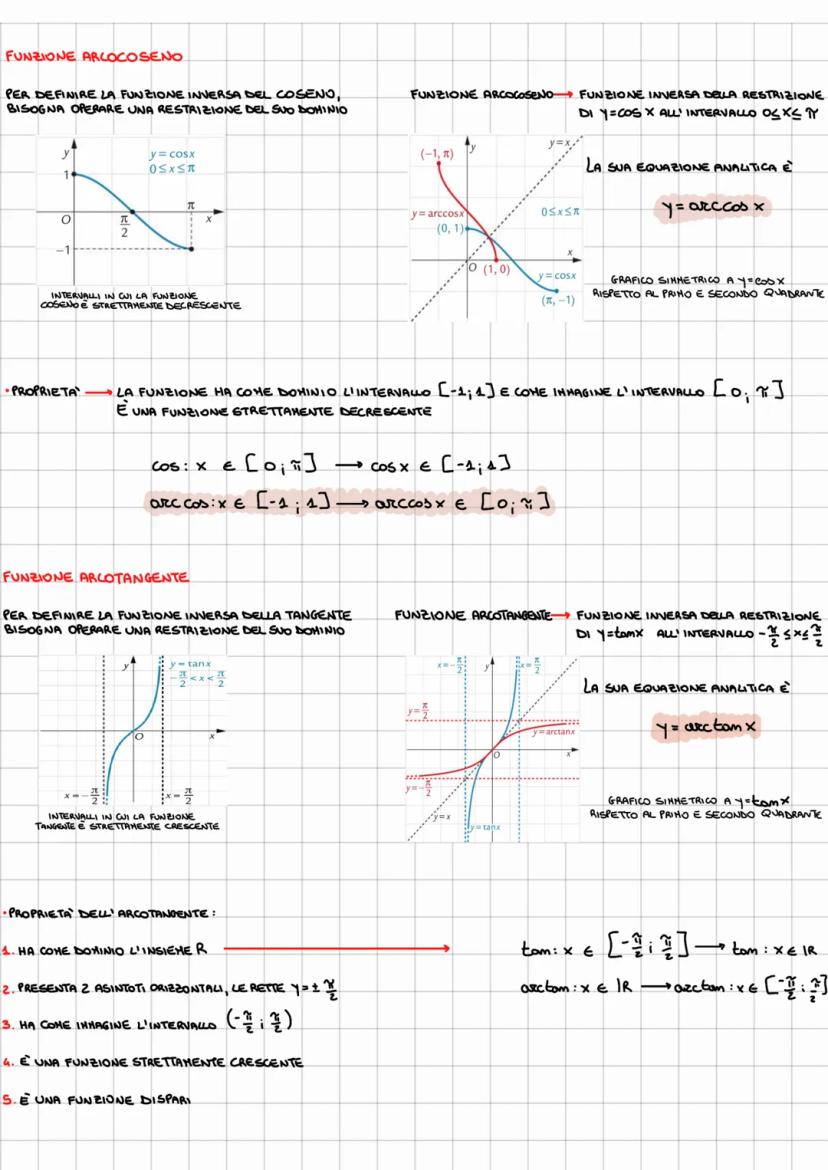
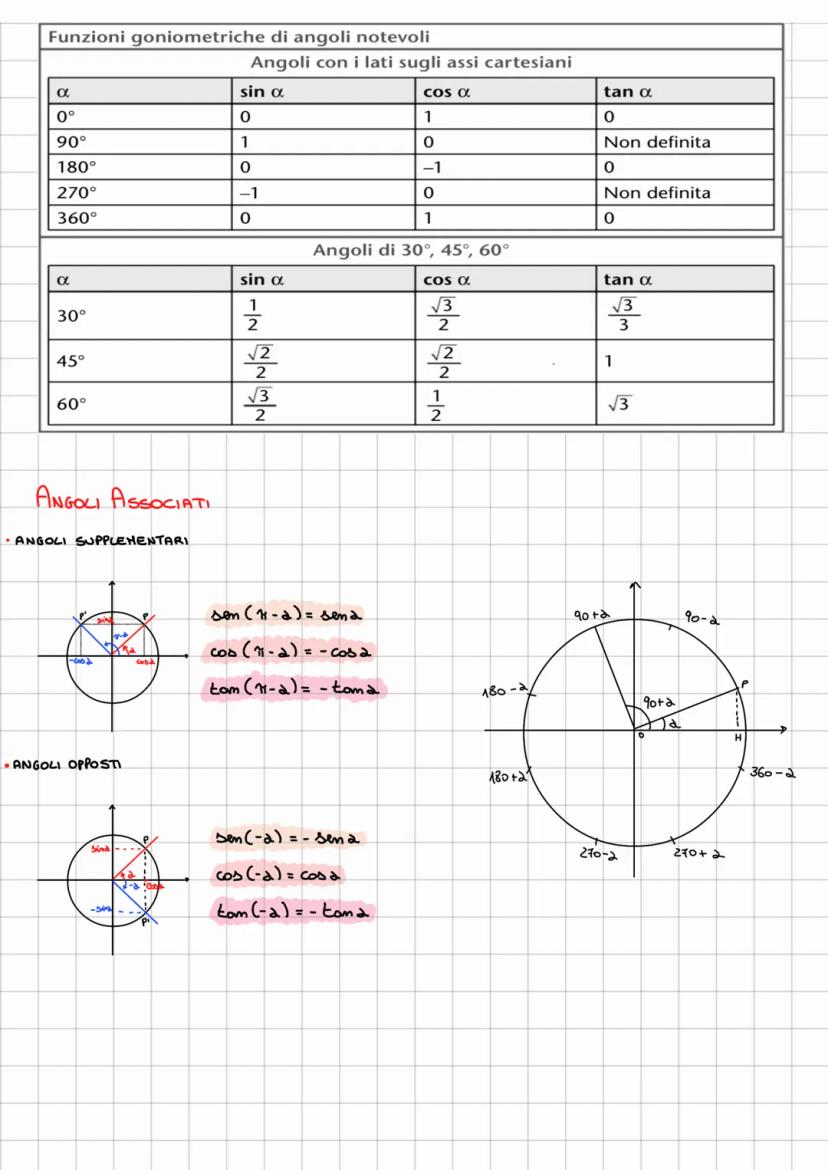
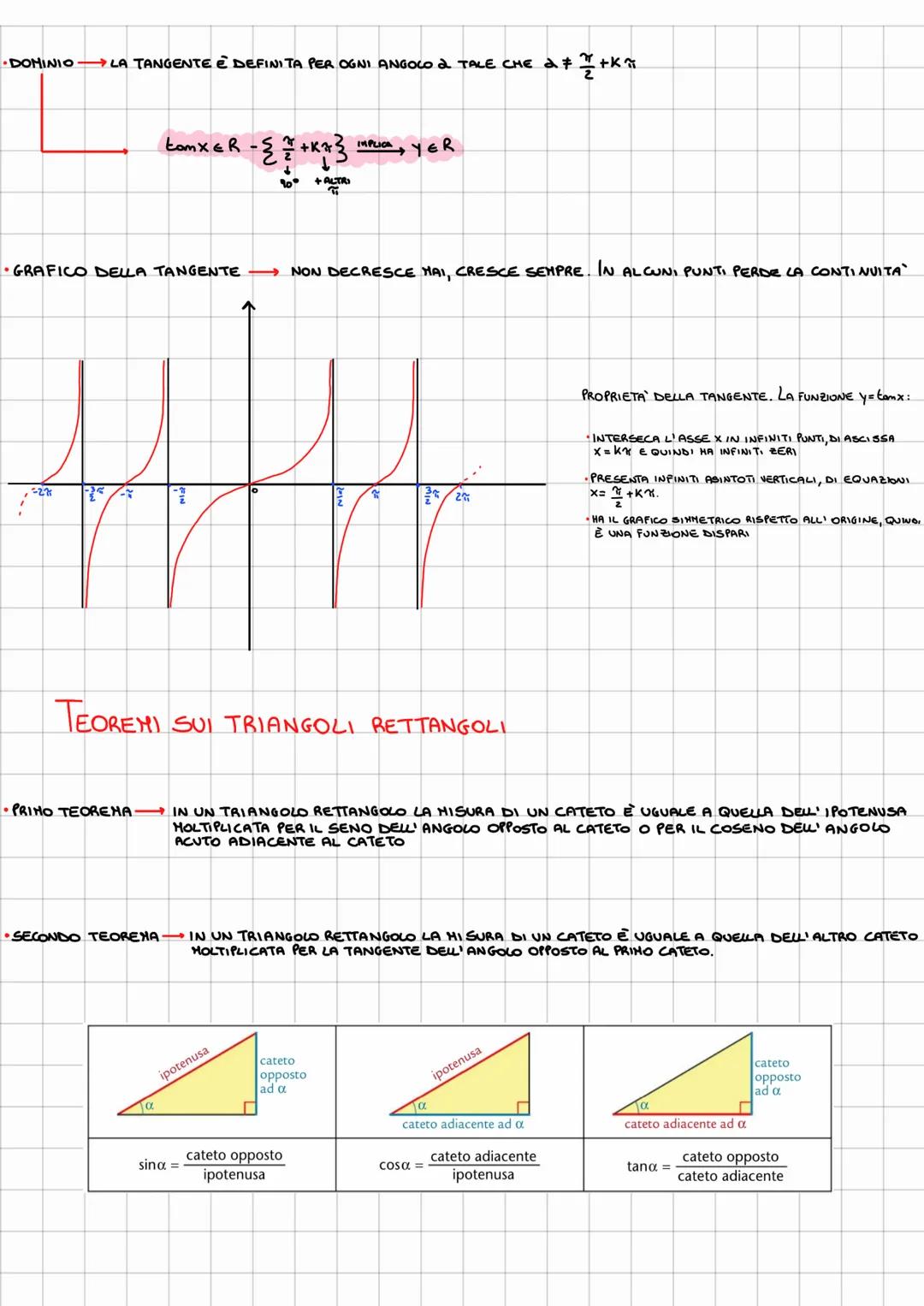
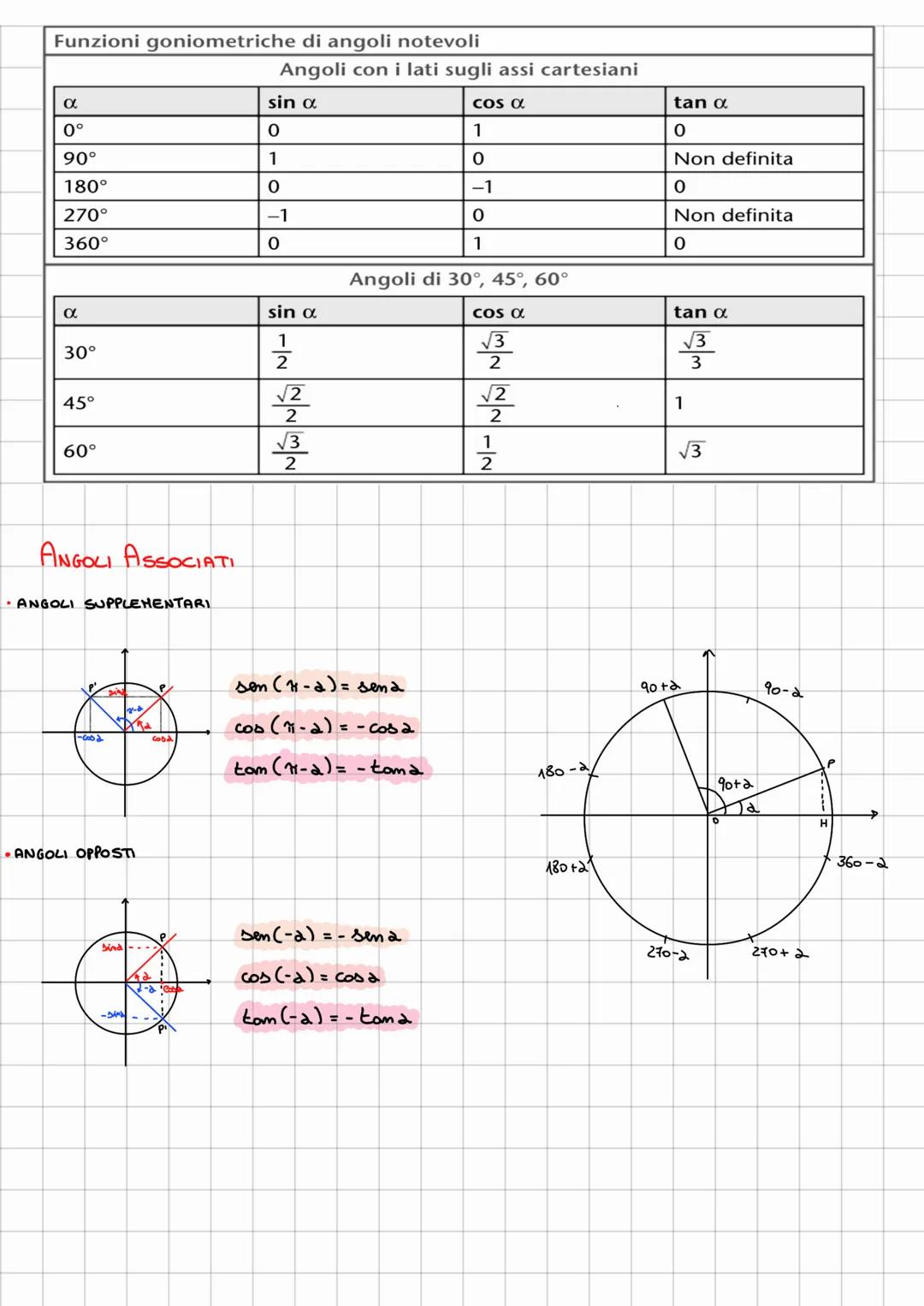
Gli angoli associati sfruttano le simmetrie della circonferenza goniometrica. Per angoli supplementari (π - α): il seno resta uguale, coseno e tangente cambiano segno.
Per angoli opposti (-α): il seno e la tangente cambiano segno, il coseno rimane uguale. Questo riflette il fatto che seno e tangente sono funzioni dispari, il coseno è pari.
La tabella degli angoli notevoli è il tuo migliore amico: memorizza i valori per 0°, 30°, 45°, 60°, 90° e saprai gestire tutti gli altri usando le simmetrie!
💡 Strategia vincente: Invece di memorizzare centinaia di valori, impara bene questi pochi e usa le simmetrie per ricavare tutto il resto!