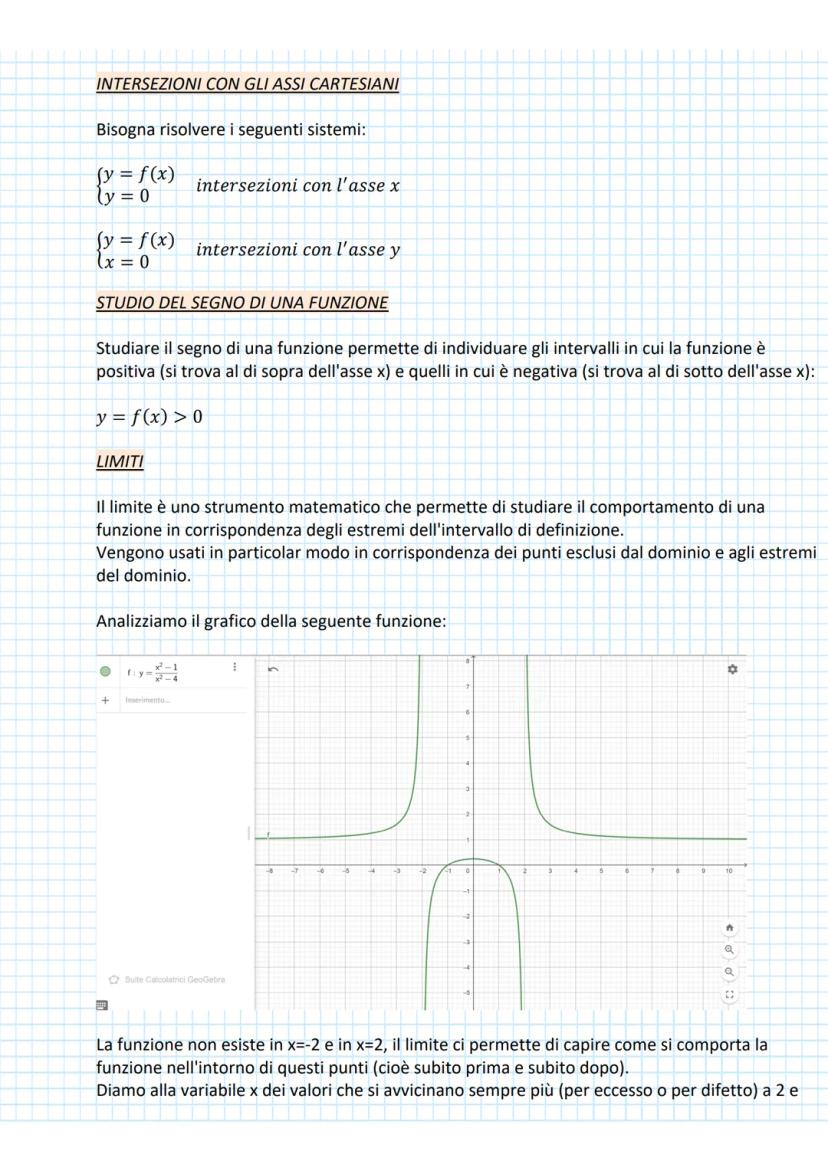
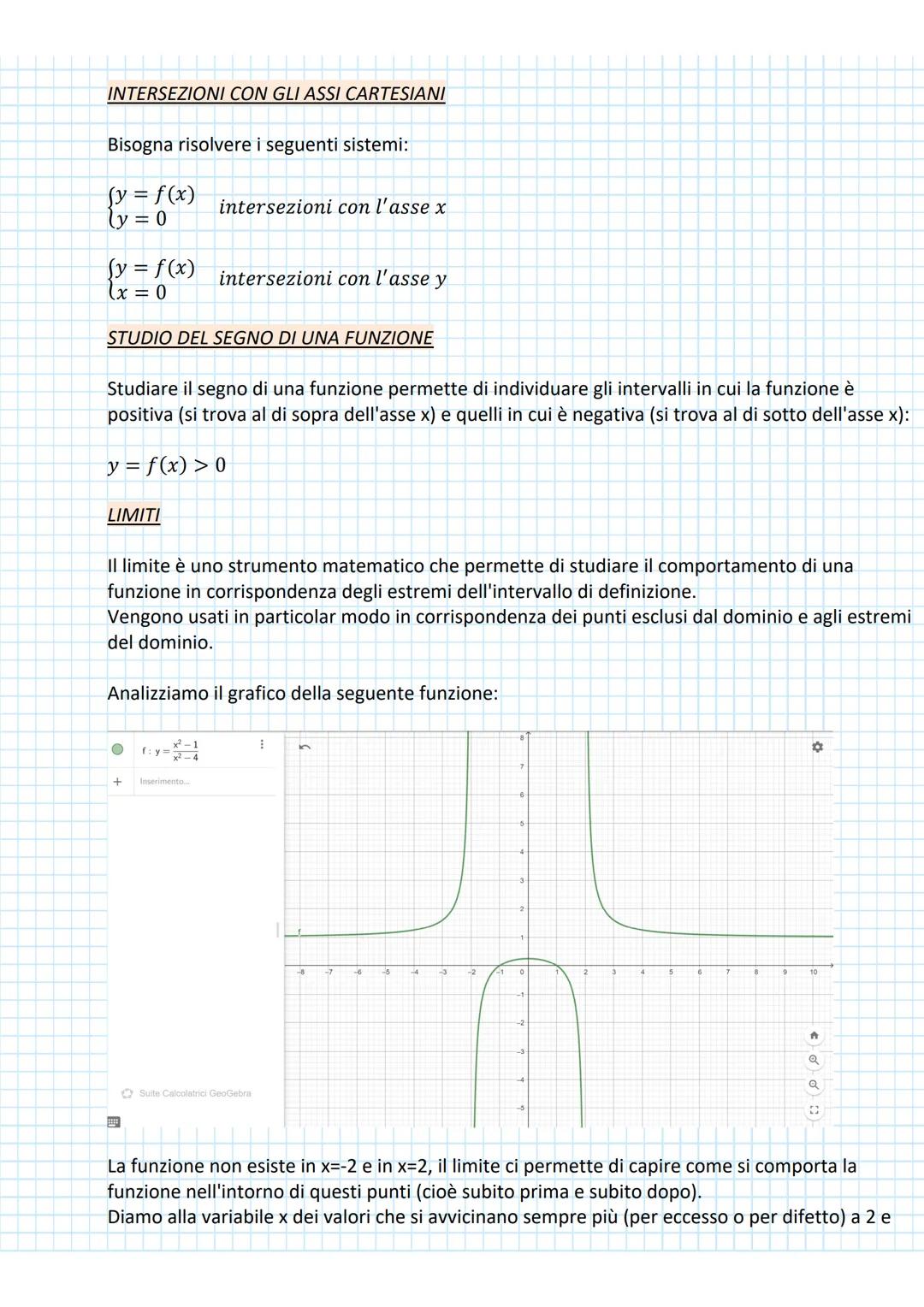
Definizione e Classificazione delle Funzioni
Pensa a una funzione come a una macchina che trasforma numeri: inserisci un valore x (variabile indipendente) e ottieni un unico valore y (variabile dipendente). È come dire che ogni x ha la sua y specifica, senza ambiguità.
Il dominio è l'insieme di tutti i valori x che puoi inserire nella funzione, mentre il codominio contiene tutti i possibili valori y che escono. Quando scrivi y = f(x), stai usando la forma esplicita; quando hai f(x,y) = 0, è la forma implicita.
Le funzioni si dividono in due grandi famiglie: algebriche cheusanosolooperazioni"normali"come+,−,×,÷,potenzeeradici e trascendenti (come logaritmi, esponenziali e funzioni goniometriche). Le algebriche si suddividono poi in razionali intere, razionali fratte e irrazionali.
💡 Tip: Per ricordare la differenza, pensa che "algebrica" significa "operazioni base", mentre "trascendente" va oltre queste operazioni!