La funzione esponenziale

Ogni volta che vedi una funzione esponenziale del tipo y = aˣ, stai guardando uno dei grafici più potenti della matematica. Il comportamento di questa funzione cambia completamente a seconda del valore della base a.

Quando a > 1 $come y = 2ˣ$, il grafico è sempre crescente e passa per il punto (0;1). Più vai verso destra sull'asse x, più la funzione "esplode" verso l'alto. Verso sinistra invece, la curva si avvicina sempre di più all'asse x senza mai toccarlo.

Se 0 < a < 1 $come y = (1/2)ˣ$, succede l'esatto contrario: la funzione è decrescente. Passa sempre per (0;1), ma questa volta cresce verso sinistra e decresce verso destra.

Ricorda: Tutte le funzioni esponenziali passano per il punto (0;1) e non toccano mai l'asse x!

La funzione logaritmica

La funzione logaritmica y = log_a x è l'inversa della funzione esponenziale, e questo cambia tutto. Mentre l'esponenziale non tocca mai l'asse x, il logaritmo non tocca mai l'asse y.

Il comportamento dipende sempre dalla base: se a > 1, la funzione è crescente, se 0 < a < 1 è decrescente. Il grafico passa sempre per il punto (1;0) e ha un asintoto verticale sull'asse y.

La definizione fondamentale è questa: se aˣ = b, allora x = log_a b. Da qui derivano le proprietà essenziali che devi memorizzare: log_a 1 = 0 e log_a a = 1.

Le proprietà dei logaritmi sono i tuoi migliori alleati: log_a(b×c) = log_a b + log_a c, log_a(b/c) = log_a b - log_a c, e log_a(bⁿ) = n×log_a b.

Trucco: I logaritmi trasformano moltiplicazioni in addizioni e potenze in moltiplicazioni!

Equazioni logaritmiche

Risolvere le equazioni logaritmiche è più semplice di quanto sembri se segui sempre gli stessi tre passaggi. Prima di tutto, trova le condizioni di esistenza (l'argomento del logaritmo deve essere positivo).

Poi usa le proprietà dei logaritmi per ridurre tutto alla forma log_a(A$x$) = log_a(B$x$). A questo punto puoi "eliminare" i logaritmi e risolvere semplicemente A$x$ = B$x$.

Per equazioni del tipo log_a x = C, la soluzione è diretta: x = aᶜ. È come "spostare" il logaritmo dall'altra parte trasformandolo in esponenziale.

Nell'esempio log²x - log x - 2 = 0, sostituisci t = log x e risolvi l'equazione di secondo grado t² - t - 2 = 0. Trovi t = 2 e t = -1, quindi x = 10² = 100 e x = 10⁻¹ = 1/10.

Attenzione: Controlla sempre che le soluzioni rispettino le condizioni di esistenza!

Disequazioni logaritmiche

Le disequazioni logaritmiche seguono la stessa logica delle equazioni, ma c'è un dettaglio cruciale che fa la differenza. Dopo aver trovato le condizioni di esistenza e ridotto alla forma log_a(A$x$) ≷ log_a(B$x$), devi ricordare una regola fondamentale.

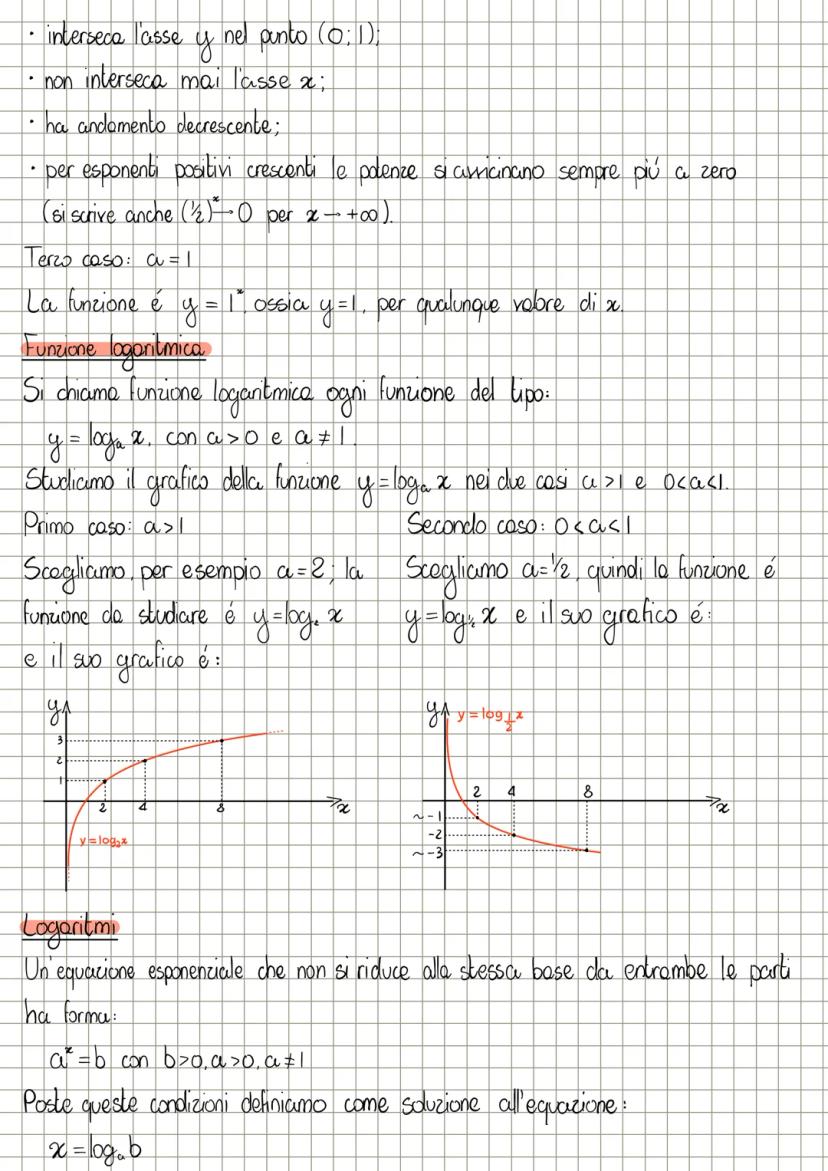
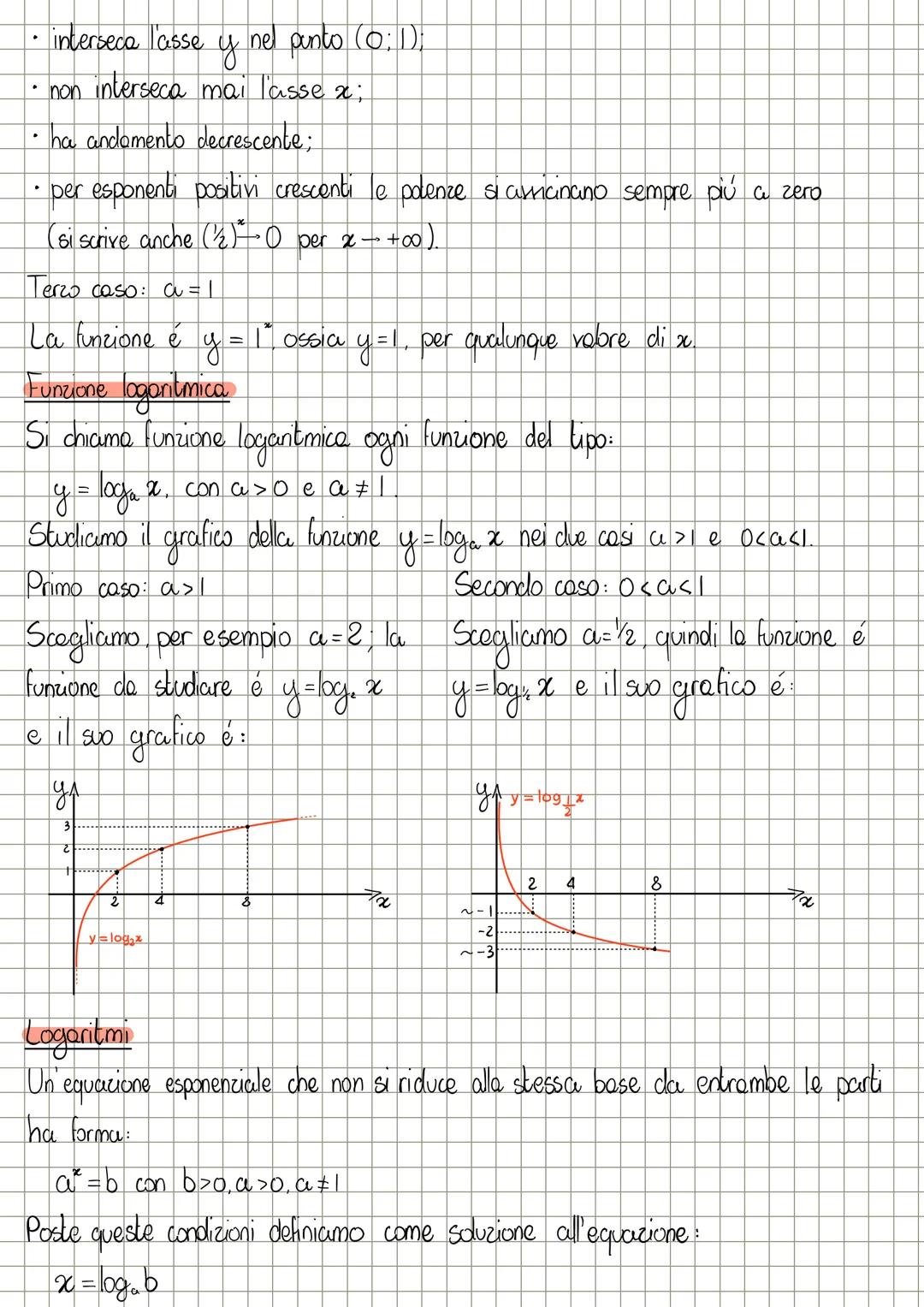
Se a > 1, la funzione logaritmica è crescente, quindi risolvi A$x$ ≷ B$x$ mantenendo il verso della disequazione. Se 0 < a < 1, la funzione è decrescente e devi invertire il verso della disequazione.

Nell'esempio log₁/₃$x-1$ < 2, prima trovi le condizioni: x > 1. Poi riscrivi 2 come log₁/₃$(1/3)²$ e ottieni log₁/₃$x-1$ < log₁/₃$1/9$.

Siccome 0 < 1/3 < 1, la funzione è decrescente, quindi investi: x-1 > 1/9, da cui x > 10/9.

Regola d'oro: Base maggiore di 1 = mantieni il verso; base minore di 1 = inverti il verso!

Condizioni di esistenza e soluzioni finali

Il passaggio finale è sempre quello più delicato: devi combinare la soluzione della disequazione con le condizioni di esistenza. Non puoi mai dimenticare questo step, altrimenti rischi di includere valori che rendono indefinita la funzione originale.

Nell'esempio precedente, avevi trovato x > 10/9 dalla disequazione e x > 1 dalle condizioni di esistenza. Il sistema da risolvere è quindi l'intersezione di questi due vincoli.

Dato che 10/9 ≈ 1,11 > 1, la soluzione finale è semplicemente x > 10/9. Le condizioni di esistenza erano già soddisfatte dalla soluzione della disequazione.

Controllo finale: Verifica sempre che la tua soluzione finale rispetti tutti i vincoli iniziali!