Iscriviti per mostrare il contenutoÈ gratis!
Accesso a tutti i documenti
Migliora i tuoi voti
Unisciti a milioni di studenti
Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.
Materie
Capolavori della Letteratura Italiana
Poesia Italiana Classica
Movimenti Artistici Italiani
Autori del Novecento Italiano
Elementi Grammaticali Fondamentali
Eroi Letterari Cavallereschi
Teatro di Goldoni
Tradizioni Familiari Italiane
Varietà Linguistiche Italiane
Innovazione Scientifica Italiana
Mostra tutti gli argomenti
La Civiltà dell'Antica Roma
Imperatori e Cronisti dell'Antica Roma
L'Unificazione e l'Integrazione Nazionale Italiana dal 1861
Monarchi e Statisti Europei
Civiltà e Culture Classiche
Le Rivoluzioni Industriali e Tecnologiche
L'Unificazione e la Costruzione dello Stato Italiano 1815-1923
Il Rinascimento e l'Illuminismo europeo
L'Era delle Guerre Mondiali e il loro Impatto
I Comuni Medievali Italiani
Mostra tutti gli argomenti
Misure del Moto e della Materia
Grandezze Vettoriali e Misurazioni
Sistemi e Unità di Misura
Operazioni con Numeri Decimali e Notazione Scientifica
Fondamenti e Sistemi Matematici
Limiti di Funzione e Asintoti
Proprietà degli Esponenti e dei Logaritmi
Funzioni e Identità Trigonometriche
Espressioni e Forme Quadratiche
Espressioni Razionali e Radicali
Mostra tutti gli argomenti
Biodiversità e Dinamiche delle Popolazioni
Cicli Ambientali e Trattamento
Astronomia di Base del Sistema Solare
Geografia Politica Mondiale
Sistemi a Celle a Combustibile a Idrogeno
Relazioni Alimentari negli Ecosistemi
Fonti di Energia e Combustibili
Vie di Trasmissione delle Malattie
Inquinanti Chimici Ambientali
Componenti ed Interazioni degli Ecosistemi
Mostra tutti gli argomenti
Le Origini della Filosofia Greca Antica
Sottodiscipline e Approcci Filosofici
La Filosofia del Rinascimento Italiano
Filosofi Occidentali Moderni
Movimenti Filosofici Moderni
La Filosofia Cristiana Medievale
Teorie Pedagogiche Filosofiche
Metodi di Acquisizione della Conoscenza
Filosofie Classiche della Vita
La Metafisica Aristotelica
Mostra tutti gli argomenti
9285
•
3 feb 2026
•
Elisa Zecca
@elisazecca_pxvm













Il nostro assistente AI è costruito specificamente per le esigenze degli studenti. Sulla base dei milioni di contenuti presenti sulla piattaforma, possiamo fornire agli studenti risposte davvero significative e pertinenti. Ma non si tratta solo di risposte, l'assistente è in grado di guidare gli studenti attraverso le loro sfide quotidiane di studio, con piani di studio personalizzati, quiz o contenuti nella chat e una personalizzazione al 100% basata sulle competenze e sugli sviluppi degli studenti.
È possibile scaricare l'applicazione dal Google Play Store e dall'Apple App Store.
Sì, hai accesso completamente gratuito a tutti i contenuti nell'app e puoi chattare o seguire i Creatori in qualsiasi momento. Sbloccherai nuove funzioni crescendo il tuo numero di follower. Inoltre, offriamo Knowunity Premium, che consente di studiare senza alcun limite!!
App Store
Google Play
L'applicazione è molto facile da usare e ben progettata. Finora ho trovato tutto quello che cercavo e ho potuto imparare molto dalle presentazioni! Utilizzerò sicuramente l'app per i compiti in classe! È molto utile anche come fonte di ispirazione.
Stefano S
utente iOS
Questa applicazione è davvero grande! Ci sono tantissimi appunti e aiuti con lo studio [...]. La mia materia problematica, per esempio, è il francese e l'app ha così tante opzioni per aiutarmi. Grazie a questa app ho migliorato il mio francese. La consiglio a tutti.
Samantha Klich
utente Android
Wow, sono davvero stupita. Ho appena provato l'app perché l'ho vista pubblicizzata molte volte e sono rimasta assolutamente sbalordita. Questa app è L'AIUTO che cercate per la scuola e soprattutto offre tantissime cose, come allenamenti e schede, che a me personalmente sono state MOLTO utili.
Anna
utente iOS
È bellissima questa app, la adoro. È utilissima per lo studio e mi aiuta molto, anzi moltissimo, ma soprattutto mi aiutano molto i quiz, per memorizzare anche quello che non sapevo
Anastasia
utente Android
Fantastica per qualsiasi materia avere gli appunti anche di altre persone è molto utile perchè posso confrontarmi e vedere come migliorarmi. con i quiz riesco ad apprendere al meglio.
Francesca
utente Android
moooolto utile,gli appunti sono belli e funzionanti,schoolGPT da dei consigli formidabili!!
Marianna
utente Android
L'applicazione è semplicemente fantastica! Tutto ciò che devo fare è inserire l'argomento nella barra di ricerca e ottengo la risposta molto velocemente. Non devo guardare 10 video di YouTube per capire qualcosa, quindi risparmio tempo. Consigliatissima!
Sudenaz Ocak
utente Android
A scuola andavo malissimo in matematica, ma grazie a questa applicazione ora vado meglio. Vi sono molto grato per aver creato questa app.
Greenlight Bonnie
utente Android
Knowunity è un applicazione fantastica,considerando che ha degli schemi veramente molto carini e sfiziosi e che ci sono dei quiz,oltre al fatto che questa cosa dell intelligenza artificiale "school gpt" è almeno per me molto utile, perché a differenza di Chatgpt ti da le spiegazioni, ti spiega ciò che non è chiaro! Posso studiare più velocemente tramite gli schemi e che posso pubblicare io stessa gli schemi è una funzione utilissima per gli altri studenti. Knowunity è PERFETTA
Aurora
utente Android
L’app funziona benissimo e puoi trovare qualsiasi tipo di informazione. Non ho l’abbonamento ma la parte gratuita è sufficiente per uno studio approfondito.
Martina
utente iOS
I quiz E LE flashcard SONO COSÌ UTILI E ADORO Knowunity IA. È ANCHE LETTERALMENTE COME CHATGPT MA PIÙ INTELLIGENTE!! MI HA AIUTATO ANCHE COI MIEI PROBLEMI DI MASCARA!! E ANCHE CON LE MIE VERE MATERIE! OVVIO 😍😁😲🤑💗✨🎀😮
Chiara
utente IOS
Questa app è una delle migliori, nient’altro da dire.
Andrea
utente iOS
L'applicazione è molto facile da usare e ben progettata. Finora ho trovato tutto quello che cercavo e ho potuto imparare molto dalle presentazioni! Utilizzerò sicuramente l'app per i compiti in classe! È molto utile anche come fonte di ispirazione.
Stefano S
utente iOS
Questa applicazione è davvero grande! Ci sono tantissimi appunti e aiuti con lo studio [...]. La mia materia problematica, per esempio, è il francese e l'app ha così tante opzioni per aiutarmi. Grazie a questa app ho migliorato il mio francese. La consiglio a tutti.
Samantha Klich
utente Android
Wow, sono davvero stupita. Ho appena provato l'app perché l'ho vista pubblicizzata molte volte e sono rimasta assolutamente sbalordita. Questa app è L'AIUTO che cercate per la scuola e soprattutto offre tantissime cose, come allenamenti e schede, che a me personalmente sono state MOLTO utili.
Anna
utente iOS
È bellissima questa app, la adoro. È utilissima per lo studio e mi aiuta molto, anzi moltissimo, ma soprattutto mi aiutano molto i quiz, per memorizzare anche quello che non sapevo
Anastasia
utente Android
Fantastica per qualsiasi materia avere gli appunti anche di altre persone è molto utile perchè posso confrontarmi e vedere come migliorarmi. con i quiz riesco ad apprendere al meglio.
Francesca
utente Android
moooolto utile,gli appunti sono belli e funzionanti,schoolGPT da dei consigli formidabili!!
Marianna
utente Android
L'applicazione è semplicemente fantastica! Tutto ciò che devo fare è inserire l'argomento nella barra di ricerca e ottengo la risposta molto velocemente. Non devo guardare 10 video di YouTube per capire qualcosa, quindi risparmio tempo. Consigliatissima!
Sudenaz Ocak
utente Android
A scuola andavo malissimo in matematica, ma grazie a questa applicazione ora vado meglio. Vi sono molto grato per aver creato questa app.
Greenlight Bonnie
utente Android
Knowunity è un applicazione fantastica,considerando che ha degli schemi veramente molto carini e sfiziosi e che ci sono dei quiz,oltre al fatto che questa cosa dell intelligenza artificiale "school gpt" è almeno per me molto utile, perché a differenza di Chatgpt ti da le spiegazioni, ti spiega ciò che non è chiaro! Posso studiare più velocemente tramite gli schemi e che posso pubblicare io stessa gli schemi è una funzione utilissima per gli altri studenti. Knowunity è PERFETTA
Aurora
utente Android
L’app funziona benissimo e puoi trovare qualsiasi tipo di informazione. Non ho l’abbonamento ma la parte gratuita è sufficiente per uno studio approfondito.
Martina
utente iOS
I quiz E LE flashcard SONO COSÌ UTILI E ADORO Knowunity IA. È ANCHE LETTERALMENTE COME CHATGPT MA PIÙ INTELLIGENTE!! MI HA AIUTATO ANCHE COI MIEI PROBLEMI DI MASCARA!! E ANCHE CON LE MIE VERE MATERIE! OVVIO 😍😁😲🤑💗✨🎀😮
Chiara
utente IOS
Questa app è una delle migliori, nient’altro da dire.
Andrea
utente iOS

Accesso a tutti i documenti
Migliora i tuoi voti
Unisciti a milioni di studenti
Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Accesso a tutti i documenti
Migliora i tuoi voti
Unisciti a milioni di studenti
Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Accesso a tutti i documenti
Migliora i tuoi voti
Unisciti a milioni di studenti
Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Accesso a tutti i documenti
Migliora i tuoi voti
Unisciti a milioni di studenti
Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Accesso a tutti i documenti
Migliora i tuoi voti
Unisciti a milioni di studenti
Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Accesso a tutti i documenti
Migliora i tuoi voti
Unisciti a milioni di studenti
Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Accesso a tutti i documenti
Migliora i tuoi voti
Unisciti a milioni di studenti
Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.
Il nostro assistente AI è costruito specificamente per le esigenze degli studenti. Sulla base dei milioni di contenuti presenti sulla piattaforma, possiamo fornire agli studenti risposte davvero significative e pertinenti. Ma non si tratta solo di risposte, l'assistente è in grado di guidare gli studenti attraverso le loro sfide quotidiane di studio, con piani di studio personalizzati, quiz o contenuti nella chat e una personalizzazione al 100% basata sulle competenze e sugli sviluppi degli studenti.
È possibile scaricare l'applicazione dal Google Play Store e dall'Apple App Store.
Sì, hai accesso completamente gratuito a tutti i contenuti nell'app e puoi chattare o seguire i Creatori in qualsiasi momento. Sbloccherai nuove funzioni crescendo il tuo numero di follower. Inoltre, offriamo Knowunity Premium, che consente di studiare senza alcun limite!!
260
Strumenti Intelligenti NUOVO
Trasforma questi appunti in: ✓ 50+ Domande di Pratica ✓ Flashcard Interattive ✓ Simulazione d'esame completa ✓ Schemi per Saggi
Schema di matematica su tutte le forme indeterminate con esempi risolutivi.
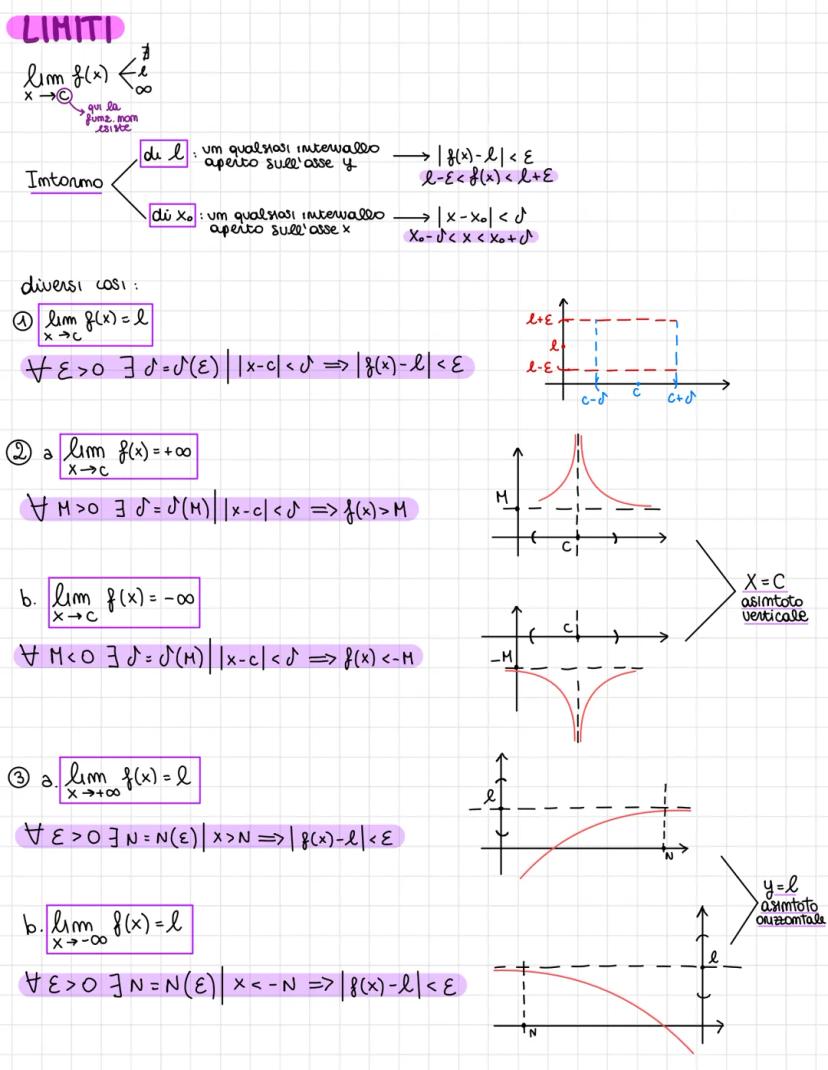
Asintoti
Appunti sui limiti, gli intorni e gli estremi (presi su goodnotes)
riassunto completo
Analisi
limiti notevoli, forme indeterminate
App Store
Google Play
L'applicazione è molto facile da usare e ben progettata. Finora ho trovato tutto quello che cercavo e ho potuto imparare molto dalle presentazioni! Utilizzerò sicuramente l'app per i compiti in classe! È molto utile anche come fonte di ispirazione.
Stefano S
utente iOS
Questa applicazione è davvero grande! Ci sono tantissimi appunti e aiuti con lo studio [...]. La mia materia problematica, per esempio, è il francese e l'app ha così tante opzioni per aiutarmi. Grazie a questa app ho migliorato il mio francese. La consiglio a tutti.
Samantha Klich
utente Android
Wow, sono davvero stupita. Ho appena provato l'app perché l'ho vista pubblicizzata molte volte e sono rimasta assolutamente sbalordita. Questa app è L'AIUTO che cercate per la scuola e soprattutto offre tantissime cose, come allenamenti e schede, che a me personalmente sono state MOLTO utili.
Anna
utente iOS
È bellissima questa app, la adoro. È utilissima per lo studio e mi aiuta molto, anzi moltissimo, ma soprattutto mi aiutano molto i quiz, per memorizzare anche quello che non sapevo
Anastasia
utente Android
Fantastica per qualsiasi materia avere gli appunti anche di altre persone è molto utile perchè posso confrontarmi e vedere come migliorarmi. con i quiz riesco ad apprendere al meglio.
Francesca
utente Android
moooolto utile,gli appunti sono belli e funzionanti,schoolGPT da dei consigli formidabili!!
Marianna
utente Android
L'applicazione è semplicemente fantastica! Tutto ciò che devo fare è inserire l'argomento nella barra di ricerca e ottengo la risposta molto velocemente. Non devo guardare 10 video di YouTube per capire qualcosa, quindi risparmio tempo. Consigliatissima!
Sudenaz Ocak
utente Android
A scuola andavo malissimo in matematica, ma grazie a questa applicazione ora vado meglio. Vi sono molto grato per aver creato questa app.
Greenlight Bonnie
utente Android
Knowunity è un applicazione fantastica,considerando che ha degli schemi veramente molto carini e sfiziosi e che ci sono dei quiz,oltre al fatto che questa cosa dell intelligenza artificiale "school gpt" è almeno per me molto utile, perché a differenza di Chatgpt ti da le spiegazioni, ti spiega ciò che non è chiaro! Posso studiare più velocemente tramite gli schemi e che posso pubblicare io stessa gli schemi è una funzione utilissima per gli altri studenti. Knowunity è PERFETTA
Aurora
utente Android
L’app funziona benissimo e puoi trovare qualsiasi tipo di informazione. Non ho l’abbonamento ma la parte gratuita è sufficiente per uno studio approfondito.
Martina
utente iOS
I quiz E LE flashcard SONO COSÌ UTILI E ADORO Knowunity IA. È ANCHE LETTERALMENTE COME CHATGPT MA PIÙ INTELLIGENTE!! MI HA AIUTATO ANCHE COI MIEI PROBLEMI DI MASCARA!! E ANCHE CON LE MIE VERE MATERIE! OVVIO 😍😁😲🤑💗✨🎀😮
Chiara
utente IOS
Questa app è una delle migliori, nient’altro da dire.
Andrea
utente iOS
L'applicazione è molto facile da usare e ben progettata. Finora ho trovato tutto quello che cercavo e ho potuto imparare molto dalle presentazioni! Utilizzerò sicuramente l'app per i compiti in classe! È molto utile anche come fonte di ispirazione.
Stefano S
utente iOS
Questa applicazione è davvero grande! Ci sono tantissimi appunti e aiuti con lo studio [...]. La mia materia problematica, per esempio, è il francese e l'app ha così tante opzioni per aiutarmi. Grazie a questa app ho migliorato il mio francese. La consiglio a tutti.
Samantha Klich
utente Android
Wow, sono davvero stupita. Ho appena provato l'app perché l'ho vista pubblicizzata molte volte e sono rimasta assolutamente sbalordita. Questa app è L'AIUTO che cercate per la scuola e soprattutto offre tantissime cose, come allenamenti e schede, che a me personalmente sono state MOLTO utili.
Anna
utente iOS
È bellissima questa app, la adoro. È utilissima per lo studio e mi aiuta molto, anzi moltissimo, ma soprattutto mi aiutano molto i quiz, per memorizzare anche quello che non sapevo
Anastasia
utente Android
Fantastica per qualsiasi materia avere gli appunti anche di altre persone è molto utile perchè posso confrontarmi e vedere come migliorarmi. con i quiz riesco ad apprendere al meglio.
Francesca
utente Android
moooolto utile,gli appunti sono belli e funzionanti,schoolGPT da dei consigli formidabili!!
Marianna
utente Android
L'applicazione è semplicemente fantastica! Tutto ciò che devo fare è inserire l'argomento nella barra di ricerca e ottengo la risposta molto velocemente. Non devo guardare 10 video di YouTube per capire qualcosa, quindi risparmio tempo. Consigliatissima!
Sudenaz Ocak
utente Android
A scuola andavo malissimo in matematica, ma grazie a questa applicazione ora vado meglio. Vi sono molto grato per aver creato questa app.
Greenlight Bonnie
utente Android
Knowunity è un applicazione fantastica,considerando che ha degli schemi veramente molto carini e sfiziosi e che ci sono dei quiz,oltre al fatto che questa cosa dell intelligenza artificiale "school gpt" è almeno per me molto utile, perché a differenza di Chatgpt ti da le spiegazioni, ti spiega ciò che non è chiaro! Posso studiare più velocemente tramite gli schemi e che posso pubblicare io stessa gli schemi è una funzione utilissima per gli altri studenti. Knowunity è PERFETTA
Aurora
utente Android
L’app funziona benissimo e puoi trovare qualsiasi tipo di informazione. Non ho l’abbonamento ma la parte gratuita è sufficiente per uno studio approfondito.
Martina
utente iOS
I quiz E LE flashcard SONO COSÌ UTILI E ADORO Knowunity IA. È ANCHE LETTERALMENTE COME CHATGPT MA PIÙ INTELLIGENTE!! MI HA AIUTATO ANCHE COI MIEI PROBLEMI DI MASCARA!! E ANCHE CON LE MIE VERE MATERIE! OVVIO 😍😁😲🤑💗✨🎀😮
Chiara
utente IOS
Questa app è una delle migliori, nient’altro da dire.
Andrea
utente iOS