Valori Notevoli delle Funzioni Trigonometriche
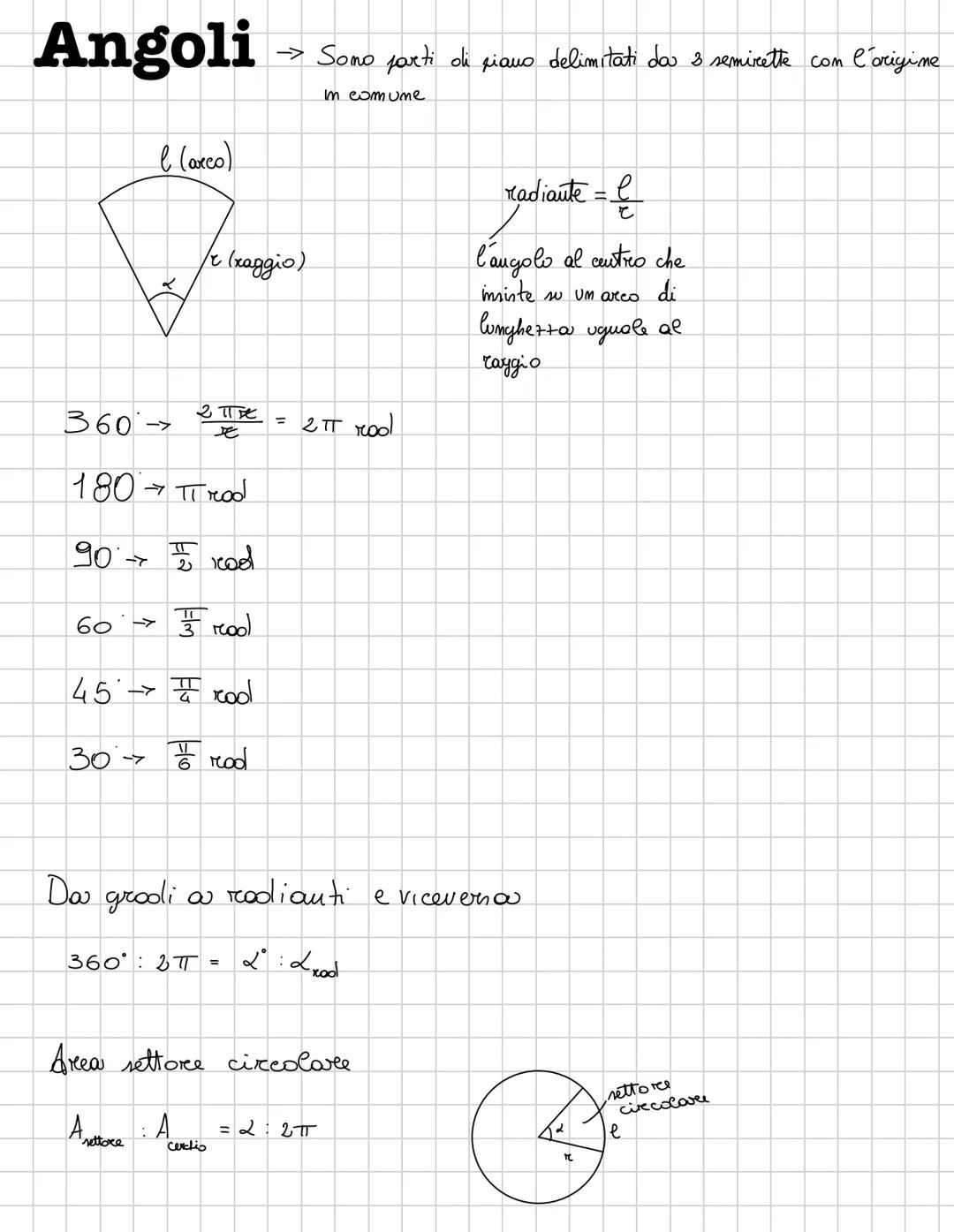
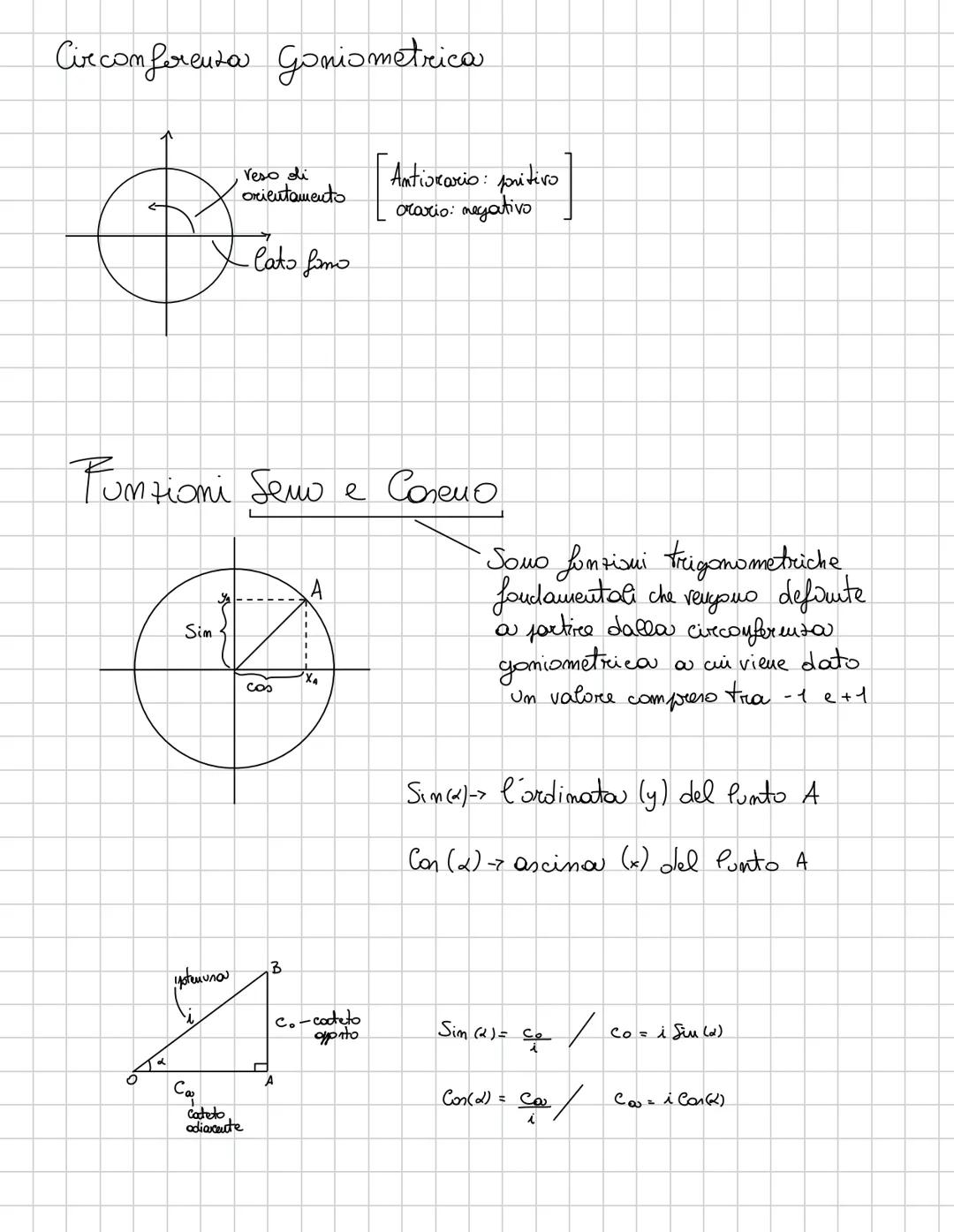
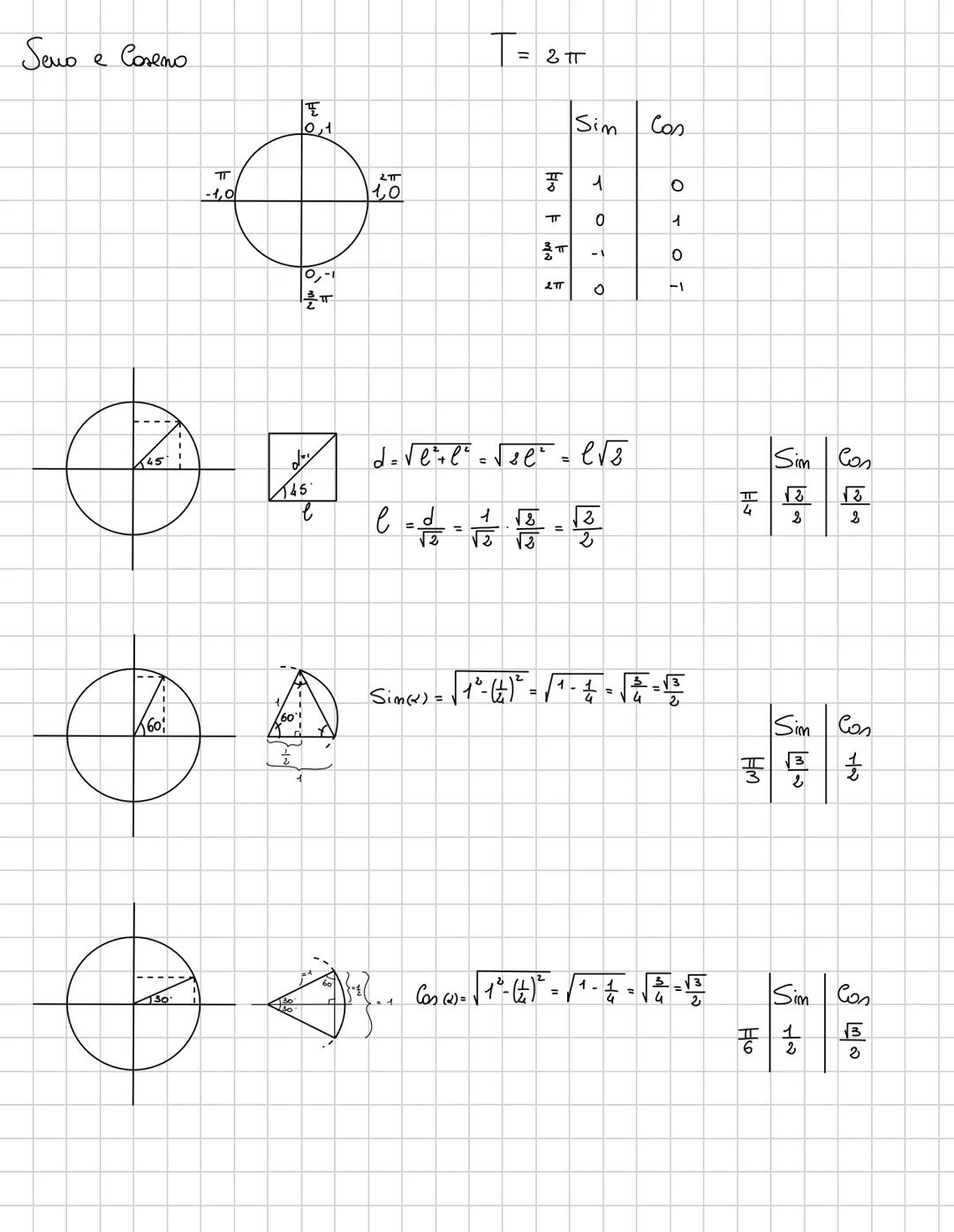
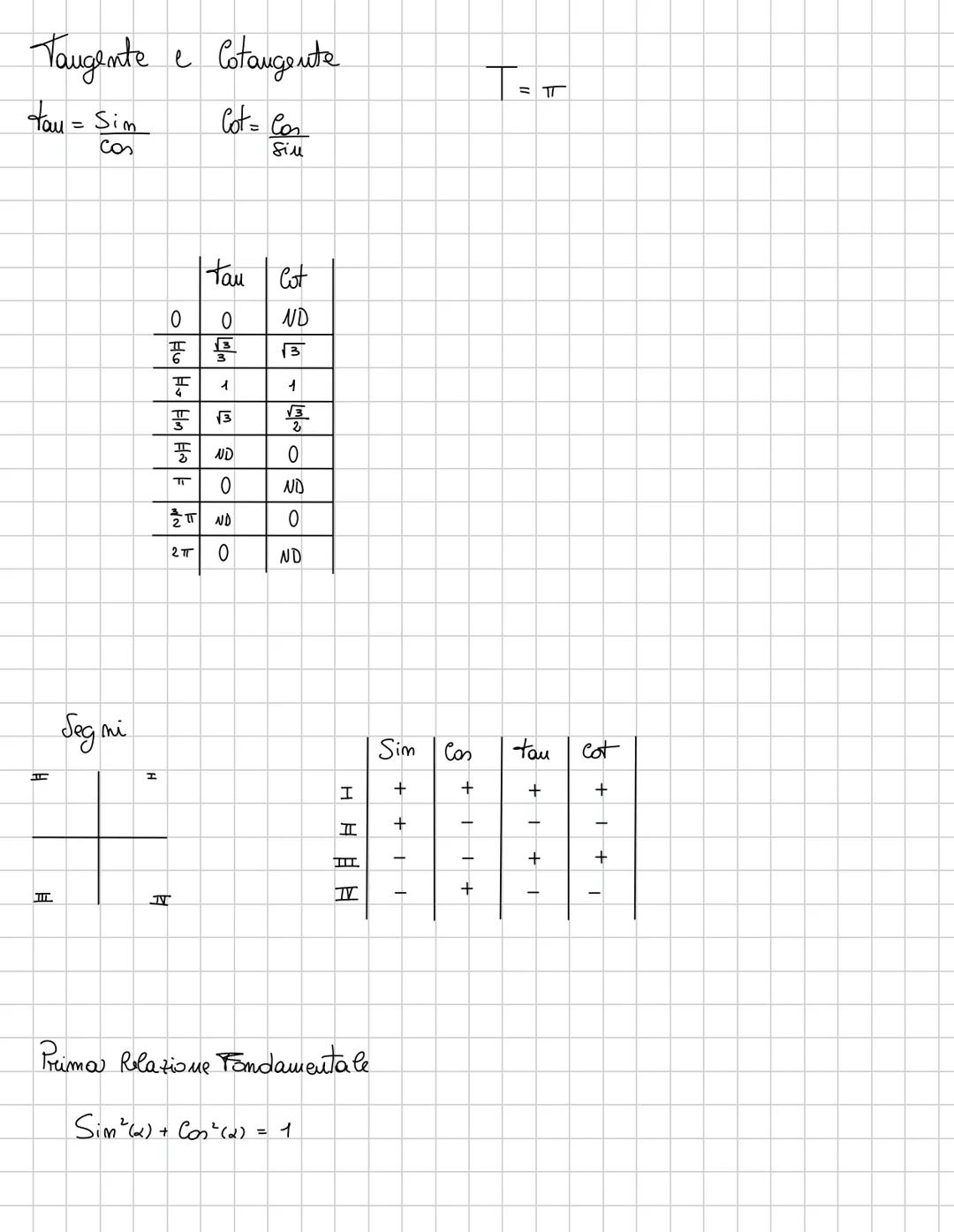
Questi sono i valori che DEVI sapere a memoria per l'esame! Per gli angoli di 30°, 45° e 60° π/6,π/4,π/3radianti, i valori sono standardizzati.
Per 45°: sin(45°) = cos(45°) = √2/2. Per 30°: sin(30°) = 1/2, cos(30°) = √3/2. Per 60°: sin(60°) = √3/2, cos(60°) = 1/2.
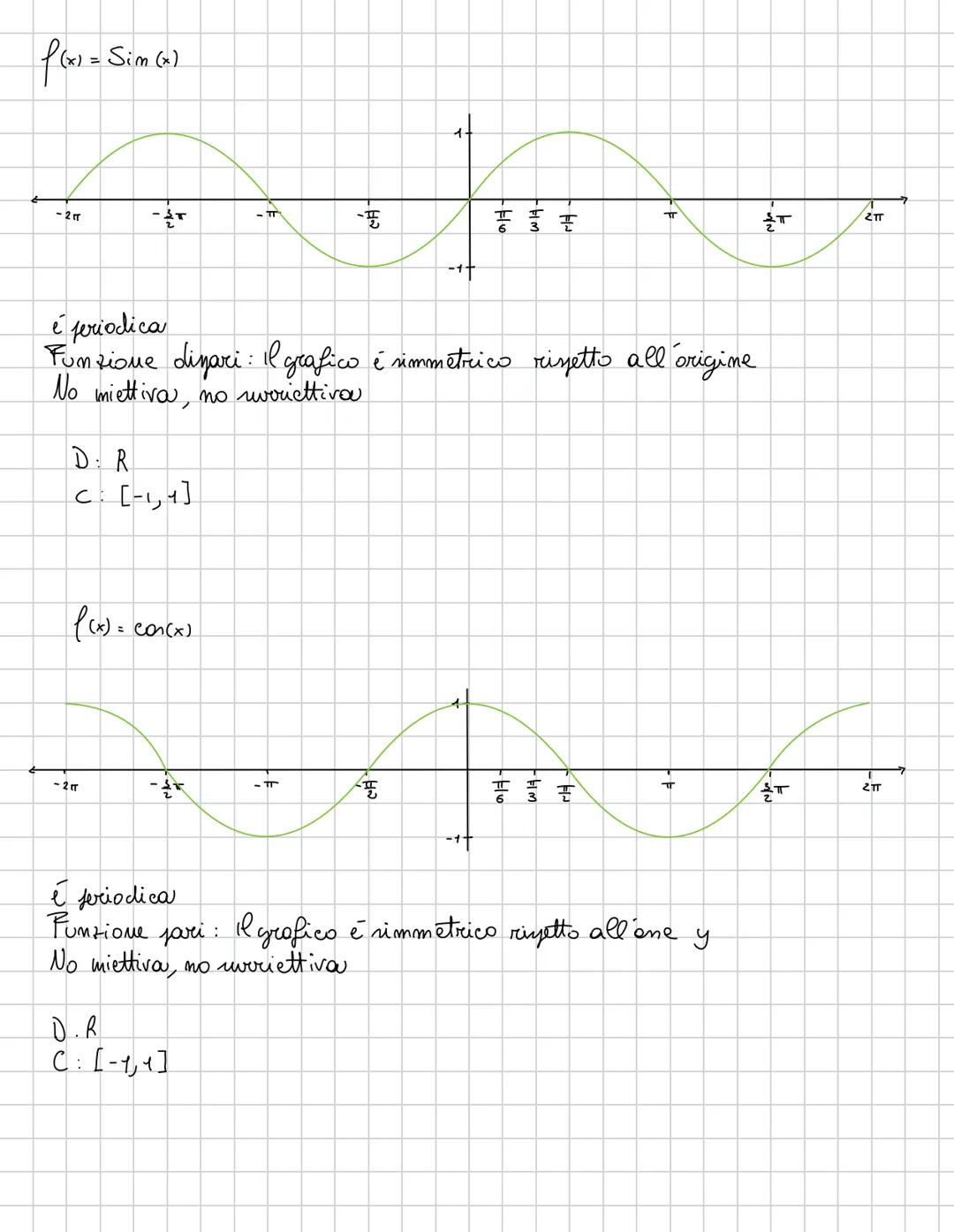
Il periodo di seno e coseno è 2π, il che significa che i valori si ripetono ogni 2π radianti. A 0 e 2π: sin = 0, cos = 1. A π/2: sin = 1, cos = 0. A π: sin = 0, cos = -1. A 3π/2: sin = -1, cos = 0.
Metodo mnemonico: Per ricordare i valori, pensa a √0/2, √1/2, √2/2, √3/2, √4/2 e semplifica!