Matematica

Espressioni e Forme Quadratiche

Equazione di Secondo Grado

Matematica7688Aggiornato 6 ott 20266 pagine

Equazioni di Secondo Grado - Esempi e Definizioni

Segnala

Doriana Tomeo@dorianatomeo_

Aggiungi alle fonti Google

Le equazioni di secondo grado sono fondamentali in matematica e ti accompagneranno per tutto il percorso scolastico. Imparerai a risolverle usando diverse tecniche e a rappresentarle graficamente attraverso le parabole.

Iscriviti per mostrare il contenuto.
È gratis!

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Equazioni di secondo grado: le basi

Un'equazione di secondo grado ha sempre la forma ax² + bx + c = 0 dove a ≠ 0. Qui x è l'incognita, mentre a, b e c sono i coefficienti dell'equazione (c si chiama anche termine noto).

Se tutti i coefficienti sono diversi da zero, l'equazione è completa. Altrimenti è incompleta e diventa più facile da risolvere. Ricorda che ogni equazione di secondo grado ha sempre due soluzioni, chiamate radici.

Le equazioni incomplete si dividono in tre tipi. Le equazioni spurie (ax² + bx = 0) si risolvono raccogliendo x e danno sempre una soluzione nulla e una reale. Le equazioni pure $ax² + c = 0$ danno due soluzioni opposte se -c/a ≥ 0, altrimenti sono impossibili.

Trucco: Nelle equazioni incomplete, riconosci subito il tipo guardando quali termini mancano - ti farà risparmiare tempo prezioso!

Per le equazioni complete, usi la formula del discriminante: Δ = b² - 4ac. Se Δ < 0 non ci sono soluzioni reali, se Δ = 0 hai due soluzioni uguali, se Δ > 0 hai due soluzioni distinte.

Iscriviti per mostrare il contenuto.
È gratis!

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Formula ridotta e relazioni tra radici

Quando il coefficiente b è pari, usa la formula ridotta che semplifica i calcoli. Invece di b usi b/2 nel discriminante: Δ = $b/2$ ² - ac, e la formula diventa x = $-b/2 ± √Δ$ /a.

Le relazioni tra radici e coefficienti sono super utili. La somma delle radici è sempre x₁ + x₂ = -b/a, mentre il prodotto è x₁ × x₂ = c/a. Queste formule ti permettono di trovare le soluzioni senza calcolare il discriminante!

Puoi anche fare il processo inverso: se conosci somma e prodotto delle radici, scrivi l'equazione come x² - (somma)x + (prodotto) = 0. È un metodo velocissimo per costruire equazioni o verificare i risultati.

Attenzione: Quando usi somma e prodotto, controlla sempre che le tue radici siano corrette sostituendole nell'equazione originale.

La scomposizione del trinomio ax² + bx + c dipende dal discriminante. Se Δ ≥ 0 diventa a $x - x₁$$x - x₂$ , se Δ = 0 diventa a $x - x₁$ ², se Δ < 0 il trinomio è irriducibile.

Iscriviti per mostrare il contenuto.
È gratis!

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Scomposizioni e equazioni fratte

Per scomporre un trinomio di secondo grado, prima risolvi l'equazione associata ax² + bx + c = 0. Se trovi le radici x₁ e x₂, puoi scrivere il trinomio come a $x - x₁$$x - x₂$ .

Negli esempi vedi come x² - x - 6 diventa $x - 3$$x + 2$ dopo aver trovato le radici 3 e -2. Questo metodo funziona sempre quando il discriminante è positivo o nullo.

Le equazioni fratte richiedono più attenzione perché devi sempre controllare le condizioni di esistenza (C.E.). Prima elimini i denominatori, risolvi l'equazione risultante, poi verifichi che le soluzioni non annullino i denominatori originali.

Errore comune: Non dimenticare mai di verificare le C.E. alla fine - una soluzione che annulla il denominatore va sempre scartata!

Nel caso di denominatori che si annullano, quella soluzione è non accettabile anche se matematicamente corretta per l'equazione trasformata.

Iscriviti per mostrare il contenuto.
È gratis!

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Equazioni letterali

Le equazioni letterali contengono parametri (lettere diverse da x) e richiedono una discussione dei casi possibili. Devi sempre considerare quando il coefficiente di x² si annulla.

Per un'equazione come ax² + bx + c = 0 con parametro a, se a = 0 l'equazione diventa di primo grado. Se a ≠ 0 mantieni il secondo grado e calcoli discriminante e soluzioni in funzione del parametro.

Nelle equazioni fratte letterali il procedimento è simile, ma devi anche verificare che le soluzioni rispettino le condizioni di esistenza per ogni valore del parametro. La sintesi finale deve indicare chiaramente i valori accettabili.

Strategia vincente: Nelle equazioni letterali, organizza sempre la discussione partendo dai casi che annullano i coefficienti principali.

La discussione completa include tutti i valori del parametro e le corrispondenti soluzioni, specificando sempre quali sono accettabili.

Iscriviti per mostrare il contenuto.
È gratis!

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Rappresentazione grafica: le parabole

La funzione quadratica y = ax² ha come grafico una parabola con vertice nell'origine e asse di simmetria sull'asse y. Il parametro a determina l'apertura: più grande è |a|, più stretta è la parabola.

Se a > 0 la parabola ha la concavità verso l'alto (sorride), se a < 0 ha la concavità verso il basso (è triste). Questo dettaglio ti aiuta subito a capire l'andamento generale della funzione.

Il vertice è il punto più importante della parabola: rappresenta il minimo se a > 0 o il massimo se a < 0. Per y = ax² il vertice è sempre nell'origine (0,0).

Visualizza sempre: Disegnare un rapido schizzo della parabola ti aiuta a capire il comportamento della funzione e a verificare i tuoi calcoli.

Costruisci la tabella dei valori scegliendo punti simmetrici rispetto all'asse y, così sfrutti la simmetria della parabola e riduci i calcoli.

Iscriviti per mostrare il contenuto.
È gratis!

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Parabola completa e intersezioni

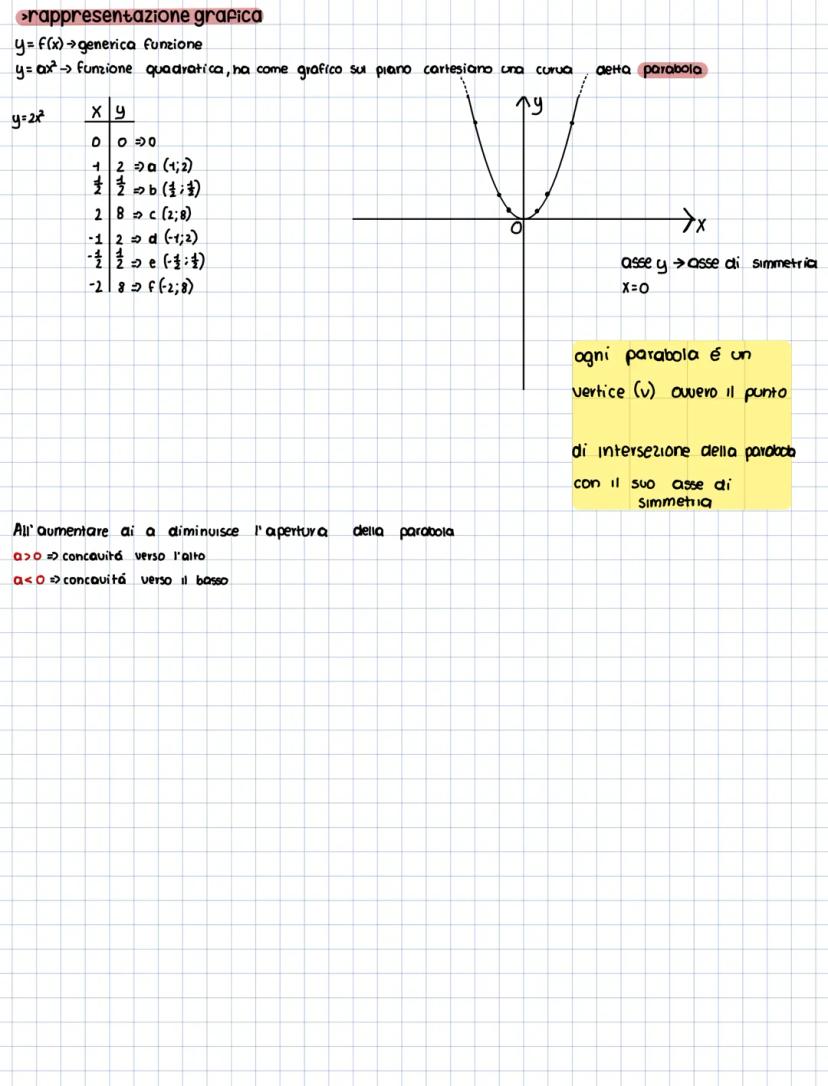
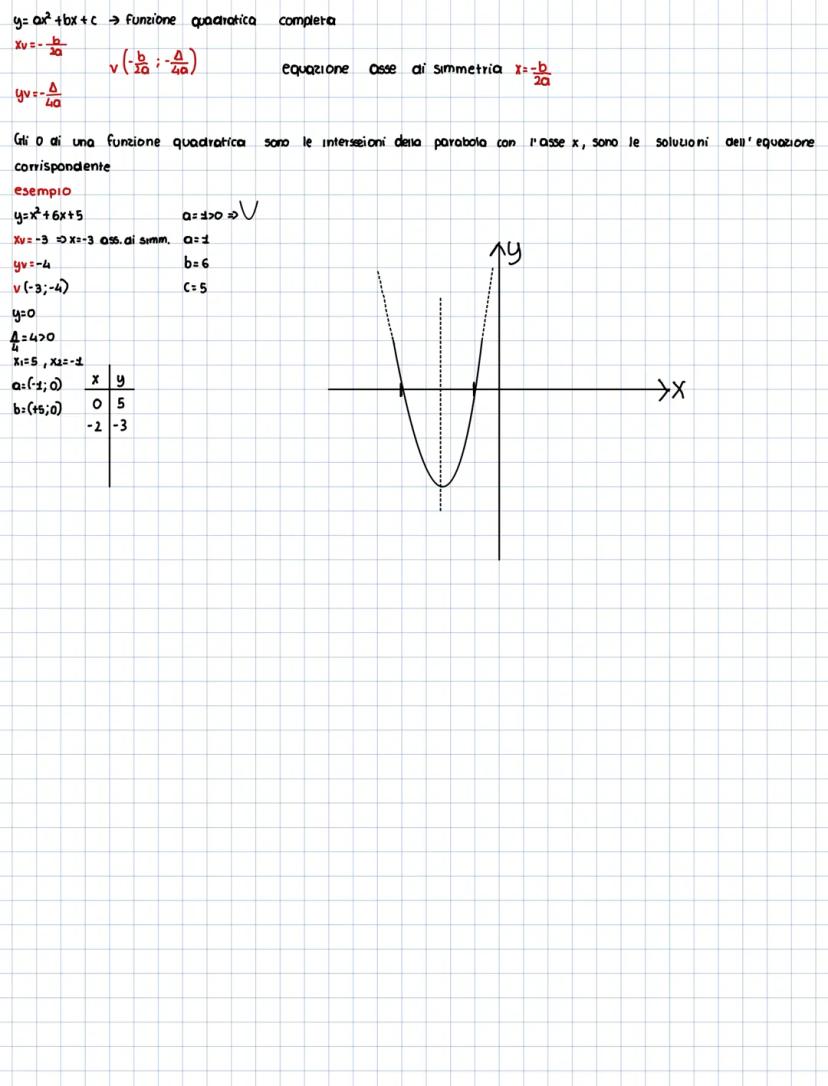
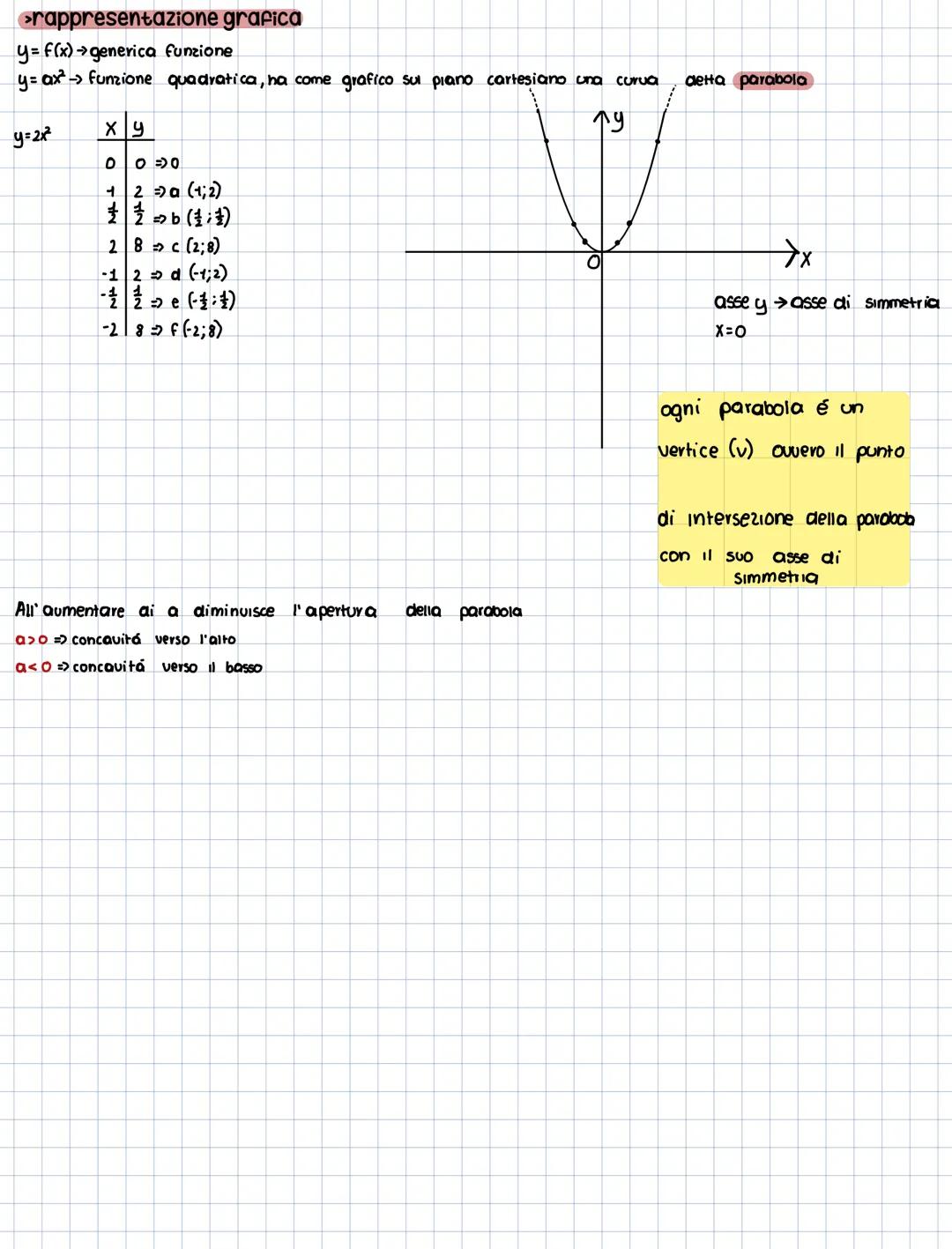
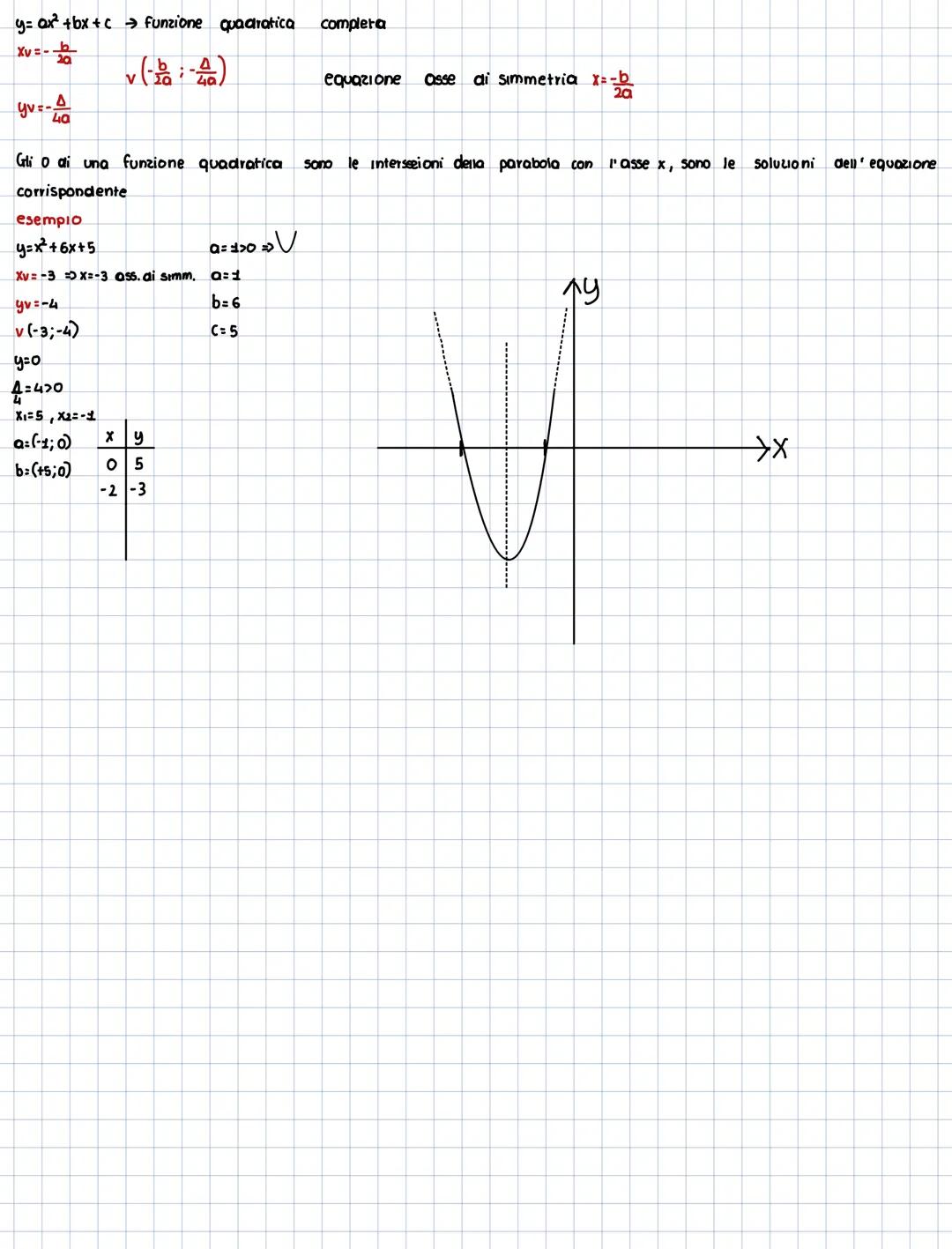
Per la funzione quadratica completa y = ax² + bx + c, il vertice ha coordinate xᵥ = -b/2a e yᵥ = -Δ/4a. L'asse di simmetria è sempre la retta verticale x = -b/2a.

Gli zeri della funzione sono i punti dove la parabola interseca l'asse x, ovvero le soluzioni dell'equazione ax² + bx + c = 0. Se Δ > 0 hai due intersezioni, se Δ = 0 una sola (tangenza), se Δ < 0 nessuna intersezione reale.

Per tracciare la parabola calcola: vertice, eventuali zeri, intersezione con l'asse y (punto (0,c)), e un paio di punti aggiuntivi per maggiore precisione. Sfrutta sempre la simmetria!

Controllo rapido: Se la parabola passa per i punti che hai calcolato e rispetta la simmetria rispetto all'asse, il grafico è corretto.

Nell'esempio con y = x² + 6x + 5, il vertice è in $-3,-4$ e gli zeri sono x = -1 e x = -5, con l'intersezione y in (0,5).

Pensavamo che non l'avreste mai chiesto....

Il nostro assistente AI è costruito specificamente per le esigenze degli studenti. Sulla base dei milioni di contenuti presenti sulla piattaforma, possiamo fornire agli studenti risposte davvero significative e pertinenti. Ma non si tratta solo di risposte, l'assistente è in grado di guidare gli studenti attraverso le loro sfide quotidiane di studio, con piani di studio personalizzati, quiz o contenuti nella chat e una personalizzazione al 100% basata sulle competenze e sugli sviluppi degli studenti.

È possibile scaricare l'applicazione dal Google Play Store e dall'Apple App Store.

Sì, hai accesso completamente gratuito a tutti i contenuti nell'app e puoi chattare o seguire i Creatori in qualsiasi momento. Sbloccherai nuove funzioni crescendo il tuo numero di follower. Inoltre, offriamo Knowunity Premium, che consente di studiare senza alcun limite!!

Equazioni di Secondo Grado - Esempi e Definizioni

Equazioni di secondo grado: le basi

Formula ridotta e relazioni tra radici

Scomposizioni e equazioni fratte

Equazioni letterali

Rappresentazione grafica: le parabole

Parabola completa e intersezioni

Pensavamo che non l'avreste mai chiesto....

Che cos'è l'assistente AI di Knowunity?

Dove posso scaricare l'applicazione Knowunity?

Knowunity è davvero gratuita?

Contenuti simili

Equaziono di II grado

equazioni di secondo grado

Equazioni di secondo grado

equazioni di secondo grado

Equazioni di secondo grado - Matematica

equazioni di secondo grado

Contenuti più popolari: Equazione di Secondo Grado

Equazioni di secondo grado

equazioni di secondo grado

Equazioni di 2° grado

equazioni secondo grado

Equazioni di secondo grado

equazioni e disequazioni

Il moto del proiettile

equazioni di secondo grado

Disequazioni di 2 grado

Contenuti più popolari: Matematica

Prima parte programma matematica test professioni sanitarie

LIMITI - APPUNTI COMPLETI CON TEOREMI

Funzioni

Preparazione Matrmatica TOLC-E

Prodotti notevoli

Formulario mate TOLC PSI

Disequazioni

Goniometria

Formulario di mate

Contenuti più popolari

Teoria patente di guida B: Segnali stradali

Riassunto patente B

Patente

Patente B / A

appunti patente

Patente B

Prima parte programma biologia test professioni sanitarie

KANT

Tutta la patente B

Recensioni dei nostri utenti. Ci adorano - e anche tu, vedrai .