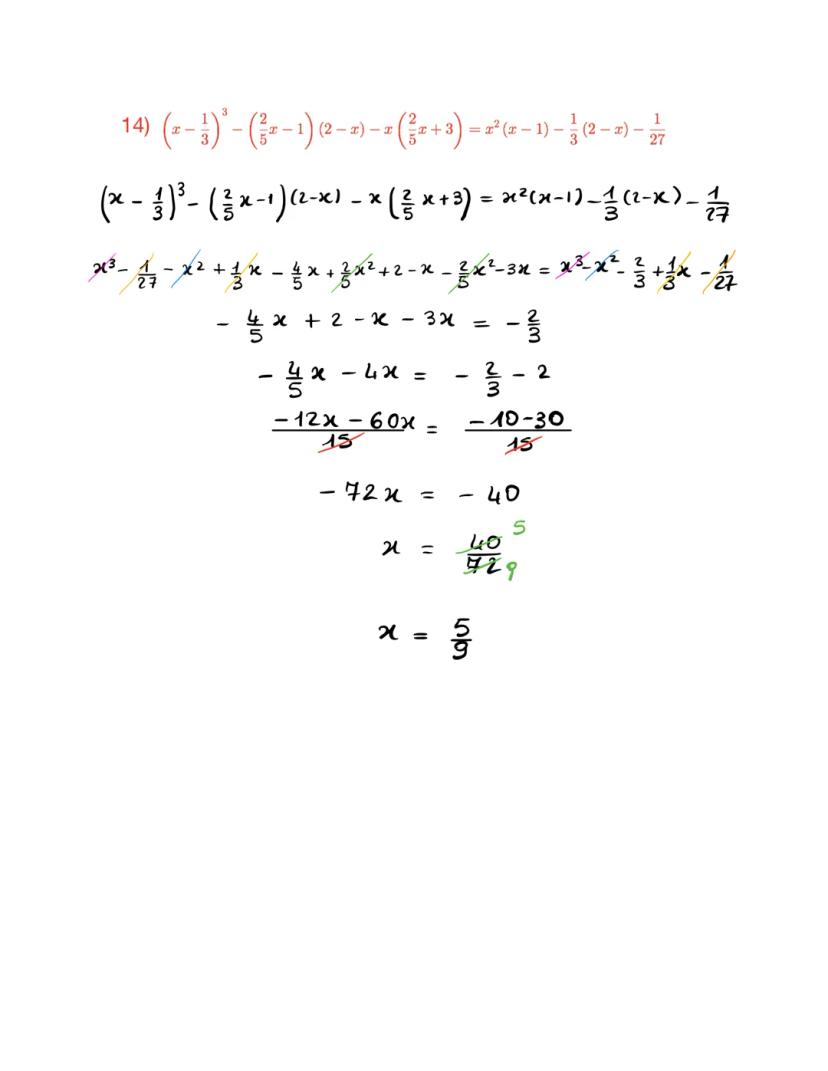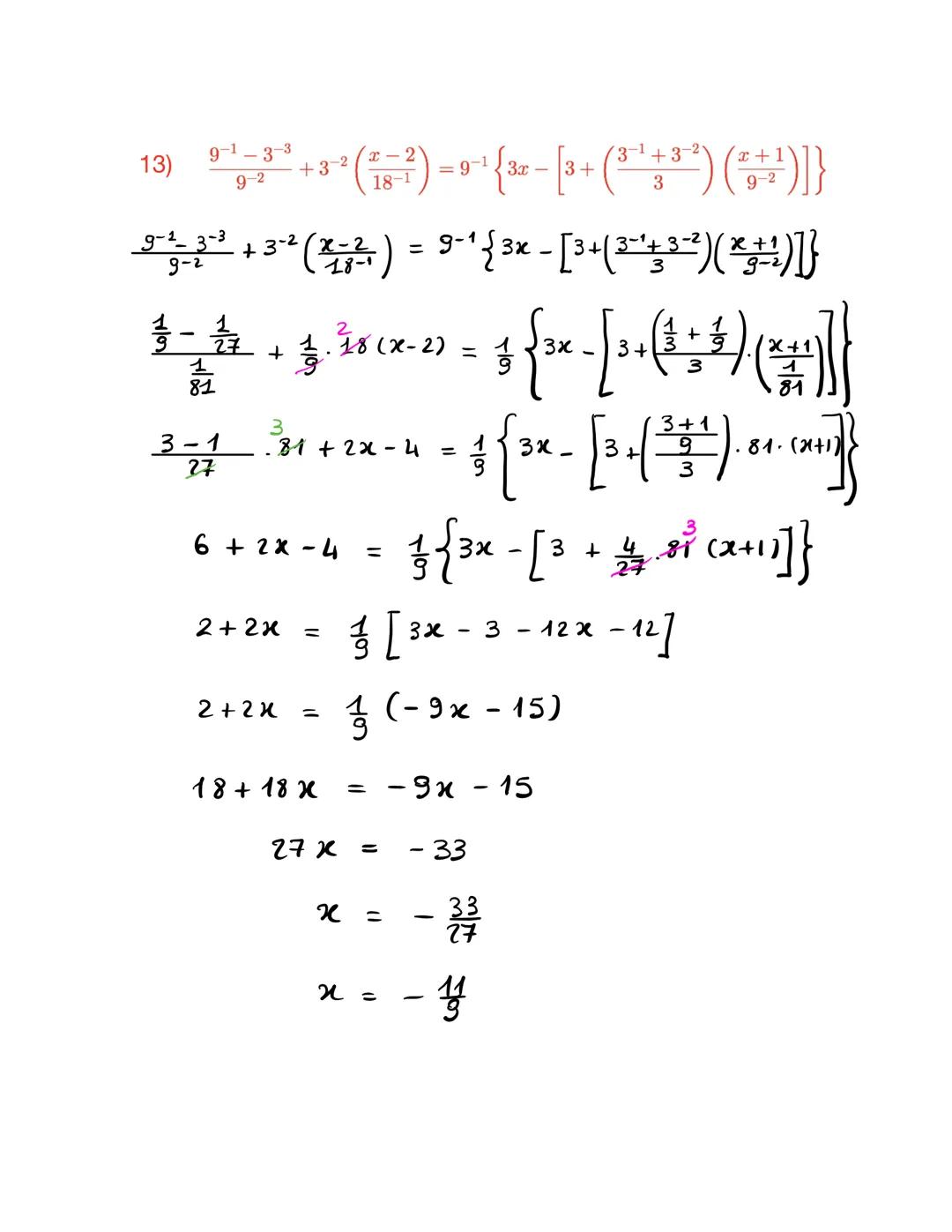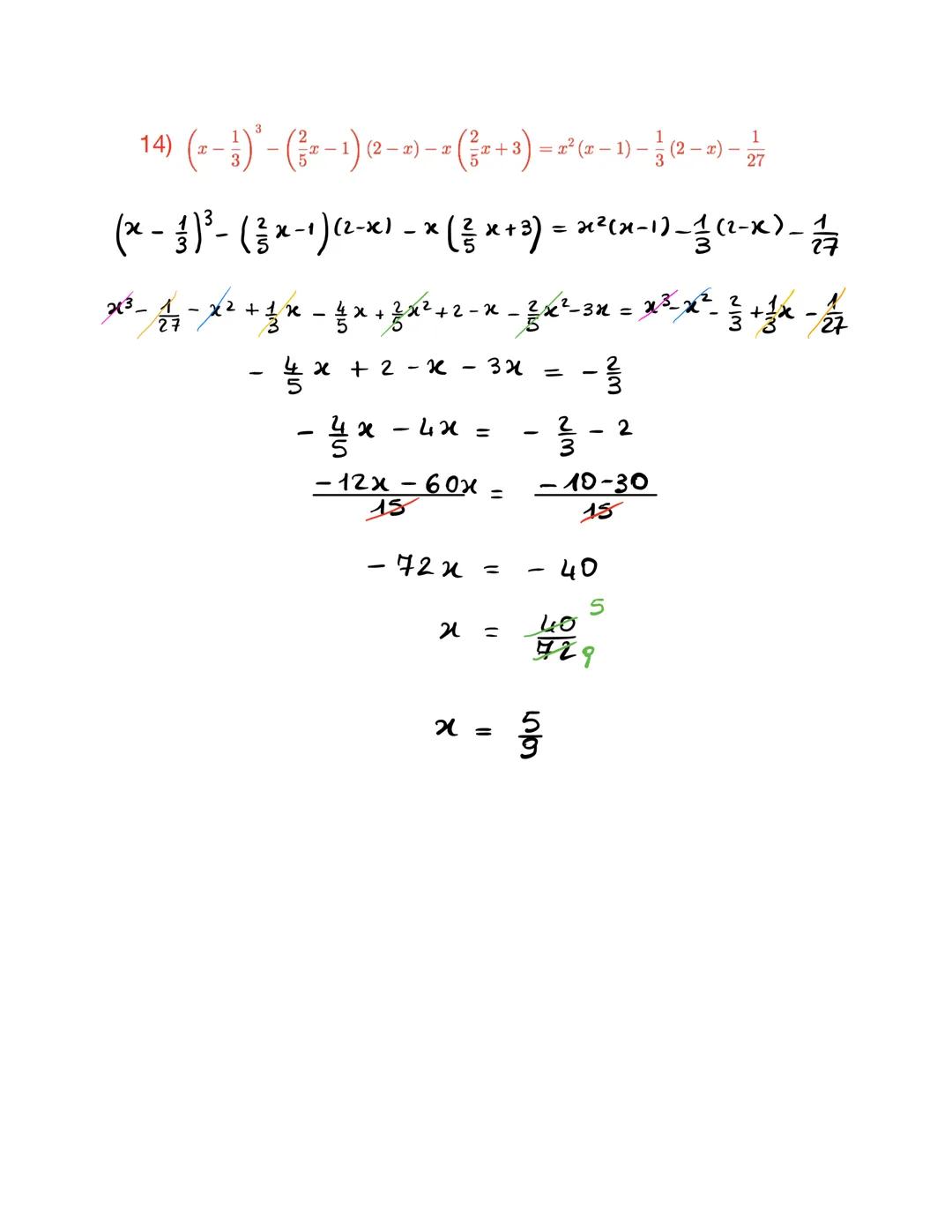Inizia

Matematica

Tecniche di Risoluzione delle Equazioni

Equazione/Disequazione a Più Passaggi

Matematica1886Aggiornato 3 set 202615 pagine

Impara le Equazioni di Primo Grado: Spiegazioni ed Esercizi

Segnala
user profile picture
Nicole@nicole.29
Aggiungi alle fonti Google
Le equazioni di primo grado sono uno strumento fondamentale della matematica che ti permette di trovare il valore incognito di una variabile. Imparerai come risolvere diversi tipi di equazioni, dalle più semplici a quelle con frazioni e parentesi complesse.
Equazioni di primo grado – pagina 1

Iscriviti per mostrare il contenuto.
È gratis!

  • Accesso a tutti i documenti
  • Migliora i tuoi voti
  • Unisciti a milioni di studenti

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Equazioni di Primo Grado - Esempi Base

Risolvere un'equazione significa trovare il valore di x che rende vera l'uguaglianza. Il trucco è spostare tutti i termini con x da una parte e i numeri dall'altra.

Nel primo esempio, dopo aver eliminato le parentesi ottieni 8x−8−2x−6=6x−3−5−17x8x - 8 - 2x - 6 = 6x - 3 - 5 - 17x. Raccogli tutti i termini con x a sinistra: 17x=617x = 6, quindi x=617x = \frac{6}{17}.

Per il secondo esempio, nota come i termini −x2-x^2 si cancellano da entrambi i lati. Questo succede spesso e semplifica molto i calcoli! Alla fine ottieni 8x=−48x = -4, quindi x=−12x = -\frac{1}{2}.

Suggerimento: Controlla sempre il tuo lavoro sostituendo il risultato nell'equazione originale!

Equazioni di primo grado – pagina 2

Iscriviti per mostrare il contenuto.
È gratis!

  • Accesso a tutti i documenti
  • Migliora i tuoi voti
  • Unisciti a milioni di studenti

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Equazioni Impossibili e Indeterminate

Non tutte le equazioni hanno una soluzione normale! Esistono due casi speciali che devi saper riconoscere.

Un'equazione impossibile si presenta quando arrivi a 0x=numero diverso da zero0x = \text{numero diverso da zero}. Nell'esempio 3, ottieni 0x=210x = 21. Dato che zero per qualsiasi numero fa sempre zero, mai 21, l'equazione non ha soluzione.

Un'equazione indeterminata si ha quando arrivi a 0x=00x = 0. Nell'esempio 4, questa situazione indica che qualsiasi valore di x è una soluzione valida - ne hai infinite!

Ricorda: 0x=numero≠00x = \text{numero} ≠ 0 = impossibile; 0x=00x = 0 = infinite soluzioni!

Equazioni di primo grado – pagina 3

Iscriviti per mostrare il contenuto.
È gratis!

  • Accesso a tutti i documenti
  • Migliora i tuoi voti
  • Unisciti a milioni di studenti

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Equazioni con Frazioni

Le equazioni fratte richiedono un passaggio extra: devi eliminare i denominatori moltiplicando tutto per il minimo comune multiplo.

Nell'esempio 5, i denominatori sono 3, 5 e 15. Il mcm è 15, quindi moltiplichi ogni termine per ottenere coefficienti interi. Dopo aver semplificato, arrivi ancora a 0x=−330x = -33 - un'altra equazione impossibile!

Il trucco è lavorare con calma e non saltare passaggi. Prima elimina le frazioni, poi procedi come al solito raccogliendo i termini simili.

Attenzione: Quando hai frazioni, il rischio di errori di calcolo aumenta - vai piano!

Equazioni di primo grado – pagina 4

Iscriviti per mostrare il contenuto.
È gratis!

  • Accesso a tutti i documenti
  • Migliora i tuoi voti
  • Unisciti a milioni di studenti

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Risoluzione Sistematica delle Frazioni

Questi esempi mostrano l'importanza di seguire una procedura ordinata quando lavori con le frazioni. Prima trovi il denominatore comune, poi moltiplichi tutto per eliminarlo.

Nell'esempio 6, il mcm di 2, 5 e 10 è 10. Moltiplichi tutto per 10 e ottieni 5(1+2x)−10x+4(x+2)=3x−55(1+2x) - 10x + 4(x+2) = 3x - 5. Semplificando: x=−18x = -18.

Per l'esempio 7, con denominatori 3, 4 e 6, il mcm è 12. Dopo la semplificazione ottieni 3x=333x = 33, quindi x=11x = 11. Vedi come il metodo funziona sempre allo stesso modo?

Strategia vincente: mcm → moltiplicare → semplificare → risolvere!

Equazioni di primo grado – pagina 5

Iscriviti per mostrare il contenuto.
È gratis!

  • Accesso a tutti i documenti
  • Migliora i tuoi voti
  • Unisciti a milioni di studenti

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Operazioni con le Frazioni - Ripasso Veloce

Prima di affrontare equazioni complesse, devi padroneggiare le operazioni tra frazioni. È la base di tutto!

Con lo stesso denominatore è facile: 52+72=5+72=122=6\frac{5}{2} + \frac{7}{2} = \frac{5+7}{2} = \frac{12}{2} = 6. Sommi solo i numeratori.

Con denominatori diversi devi trovare il mcm. Per esempio, con 52+83+78\frac{5}{2} + \frac{8}{3} + \frac{7}{8}, il mcm di 2, 3, 8 è 24. Ogni frazione diventa: 6024+6424+2124=14524\frac{60}{24} + \frac{64}{24} + \frac{21}{24} = \frac{145}{24}.

Trucco del mestiere: Se hai dubbi sul mcm, moltiplicare tutti i denominatori funziona sempre (anche se non è il modo più elegante)!

Equazioni di primo grado – pagina 6

Iscriviti per mostrare il contenuto.
È gratis!

  • Accesso a tutti i documenti
  • Migliora i tuoi voti
  • Unisciti a milioni di studenti

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Equazioni Complesse con Prodotti Notevoli

Quando incontri espressioni complesse come (4+3x)(4−3x)(4+3x)(4-3x), riconosci i prodotti notevoli! Questo è (a+b)(a−b)=a2−b2=16−9x2(a+b)(a-b) = a^2 - b^2 = 16 - 9x^2.

L'esempio 8 sembra spaventoso, ma seguendo il metodo ottieni alla fine 0x=−30x = -3. Ancora un'equazione impossibile! Non lasciarti intimidire dalla lunghezza - il processo rimane sempre uguale.

La chiave è procedere un passo alla volta: prima risolvi le parentesi interne, poi quelle esterne, infine raccogli i termini simili.

Non farti spaventare: Anche l'equazione più complessa si risolve con pazienza e metodo!

Equazioni di primo grado – pagina 7

Iscriviti per mostrare il contenuto.
È gratis!

  • Accesso a tutti i documenti
  • Migliora i tuoi voti
  • Unisciti a milioni di studenti

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Esempi con Risultati Standard

Questi esempi mostrano equazioni che portano a soluzioni normali. L'esempio 9 ti dà x=0x = 0 - un risultato pulito e semplice!

Nell'esempio 10, dopo aver lavorato con frazioni e denominatori diversi, ottieni x=−28x = -28. Nota come, nonostante la complessità iniziale, il risultato sia un numero intero.

Il prodotto notevole (2x−1)(2x+1)=4x2−1(2x-1)(2x+1) = 4x^2 - 1 semplifica molto i calcoli. Riconoscere questi pattern ti fa risparmiare tempo prezioso!

Osservazione importante: I risultati "belli" (numeri interi o frazioni semplici) spesso indicano che hai calcolato correttamente!

Equazioni di primo grado – pagina 8

Iscriviti per mostrare il contenuto.
È gratis!

  • Accesso a tutti i documenti
  • Migliora i tuoi voti
  • Unisciti a milioni di studenti

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Equazioni con Potenze Negative

Le potenze negative come 2−3=182^{-3} = \frac{1}{8} possono sembrare complicate, ma seguono regole precise. 4−2=1164^{-2} = \frac{1}{16} e (−2)−3=−18(-2)^{-3} = -\frac{1}{8}.

Nell'esempio 11, dopo aver sostituito tutti i valori e semplificato, ottieni x=2x = 2. L'esempio 12 invece porta a x=−54x = -\frac{5}{4}.

Il trucco è convertire subito le potenze negative in frazioni normali. Così eviti confusione nei calcoli successivi.

Regola d'oro: a−n=1ana^{-n} = \frac{1}{a^n} - memorizza questa formula e usala sempre!

Equazioni di primo grado – pagina 9

Iscriviti per mostrare il contenuto.
È gratis!

  • Accesso a tutti i documenti
  • Migliora i tuoi voti
  • Unisciti a milioni di studenti

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Equazioni con Potenze Complesse

Questo esempio mostra come gestire espressioni molto complesse con potenze di 3 e 9. Ricorda che 9=329 = 3^2, quindi 9−1=199^{-1} = \frac{1}{9} e 9−2=1819^{-2} = \frac{1}{81}.

La strategia vincente è semplificare tutto subito: 3−3=1273^{-3} = \frac{1}{27}, 3−1=133^{-1} = \frac{1}{3}, 3−2=193^{-2} = \frac{1}{9}. Poi procedi normalmente.

Dopo tutti i calcoli ottieni x=−119x = -\frac{11}{9}. Anche se il procedimento è lungo, il metodo rimane identico: semplifica, raccogli, risolvi.

Consiglio pratico: Con equazioni così complesse, lavora su carta abbondante e controlla ogni passaggio!

Equazioni di primo grado – pagina 10

Iscriviti per mostrare il contenuto.
È gratis!

  • Accesso a tutti i documenti
  • Migliora i tuoi voti
  • Unisciti a milioni di studenti

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Equazioni con Cubi e Espressioni Articolate

Il cubo di un binomio (x−13)3(x-\frac{1}{3})^3 si sviluppa con la formula a3−3a2b+3ab2−b3a^3 - 3a^2b + 3ab^2 - b^3. È lungo ma fattibile!

In questo esempio finale, molti termini si semplificano durante il calcolo. I termini x3x^3 e x2x^2 si cancellano, lasciando solo termini di primo grado.

Il risultato x=59x = \frac{5}{9} conferma che anche le equazioni più complesse portano spesso a soluzioni relativamente semplici.

Messaggio finale: Non importa quanto sembri complicata un'equazione - con metodo e pazienza, la risolverai sempre!

Pensavamo che non l'avreste mai chiesto....

Il nostro assistente AI è costruito specificamente per le esigenze degli studenti. Sulla base dei milioni di contenuti presenti sulla piattaforma, possiamo fornire agli studenti risposte davvero significative e pertinenti. Ma non si tratta solo di risposte, l'assistente è in grado di guidare gli studenti attraverso le loro sfide quotidiane di studio, con piani di studio personalizzati, quiz o contenuti nella chat e una personalizzazione al 100% basata sulle competenze e sugli sviluppi degli studenti.

È possibile scaricare l'applicazione dal Google Play Store e dall'Apple App Store.

Sì, hai accesso completamente gratuito a tutti i contenuti nell'app e puoi chattare o seguire i Creatori in qualsiasi momento. Sbloccherai nuove funzioni crescendo il tuo numero di follower. Inoltre, offriamo Knowunity Premium, che consente di studiare senza alcun limite!!

Contenuti simili

Fisica

Circuiti elettrici

Circuiti, lavoro, formule, nodi e rami del circuito, Kirchoff, esercizi ed esempi

3ªl7937304
Fisica

La corrente elettrica

La corrente elettrica continua, intensità di corrente generatori di tensione circuiti elettrici leggi di Kirchoff leggi di ohm.

5ªl258832
Matematica

Le equazioni

Le equazioni! appunti

3ªm4527
Matematica

teoria logaritmi

Presentazione semplice e pratica dei logaritmi.

5ªl61315
Matematica

le equazioni

cosa sono, forma normale, soluzioni e radici, grado di un'equazione, equazioni equivalenti, i principi di equivalenza, regole dei principi, passi per risolvere un'equazione di primo grado, tipi di equazioni + mappa riassuntiva

3ªm96820
Matematica

La funzione esponenziale

Appunti, formule ed esercizi

4ªl77812
Vedi altro

Contenuti più popolari: Matematica

Matematica

Prima parte programma matematica test professioni sanitarie

Materiale di matematica per il test di professioni sanitarie

Università4682134
Matematica

Formulario mate TOLC PSI

Formulario di matematica per prepararsi al TOLC PSI CISIA

5ªl6620168
Matematica

Preparazione Matrmatica TOLC-E

Appunti matematica per il tollc-e. Appunti completi

5ªl12.796401
Matematica

Preparazione Tolc I

Il contenuto è un ripasso completo di tutti gli argomenti matematici e fisici su cui le domande del TOLC I si basano.

5ªl5495159
Matematica

Seconda parte programma matematica test professioni sanitarie

Materiale di matematica per test di professioni sanitarie

Università208770
Matematica

Formulario di mate

Spero possa esservi utile

3ªl5912167
Matematica

Tolc - simulazione sezione di logica - ingegneria

Alcuni esercizi silili a quelli che potrebbero capitare nella sezione di logica del tolc di Ingegneria (tolc-i). Quarto/quinto anno liceo / itis.

4ªl286265
Matematica

Prodotti notevoli

I prodotti notevoli

1ªl66.7556917
Matematica

I logaritmi e le equazioni e disequazioni logaritmiche

I logaritmi: definizione, proprietà, esempi, equazioni e disequazioni logaritmiche

3ªl22.970786

Contenuti più popolari

Italiano

Riassunto patente B

Riassunto patente B - appunti presi a lezione

5ªl33.5231088
Altro

Teoria patente b

Tutti gli argomenti per la patente

1ªl24.557772
Altro

appunti patente

appunti esame teoria patente

4ªl73.8241850
Ed. civ.

Teoria patente di guida B: Segnali stradali

Segnali stradali di pericolo, luminosi, di prescrizione, di indicazione, temporanei, complementari, pannelli integrativi, segnaletica orizzontale, segnalazioni agenti del traffico, distanza di visibilità per l‘arresto, minima di sicurezza.

5ªl44.7661814
Altro

Patente B

Schemi

4ªl13.322312
Scienze

Prima parte programma biologia test professioni sanitarie

Materiale di biologia per il test di professioni sanitarie

Università9340204
Altro

Patente

sintesi patente

4ªl79.2545420
Chimica

Programma chimica test professioni sanitarie

Materiale di chimica per test professioni sanitarie

Università7537199
Altro

🚗 Teoria Patente B Completa + Errori Frequenti Quiz 2026

Appunti completi e semplificati per superare l’esame di teoria patente B. Include errori frequenti nei quiz, spiegazioni chiare e schemi riassuntivi.

5ªl5898101

Recensioni dei nostri utenti. Ci adorano - e anche tu, vedrai .

4.6/5App Store
4.7/5Google Play
Stefano Sutente iOS

L'applicazione è molto facile da usare e ben progettata. Finora ho trovato tutto quello che cercavo e ho potuto imparare molto dalle presentazioni! Utilizzerò sicuramente l'app per i compiti in classe! È molto utile anche come fonte di ispirazione.

Samantha Klichutente Android

Questa applicazione è davvero grande! Ci sono tantissimi appunti e aiuti con lo studio [...]. La mia materia problematica, per esempio, è il francese e l'app ha così tante opzioni per aiutarmi. Grazie a questa app ho migliorato il mio francese. La consiglio a tutti.

Annautente iOS

Wow, sono davvero stupita. Ho appena provato l'app perché l'ho vista pubblicizzata molte volte e sono rimasta assolutamente sbalordita. Questa app è L'AIUTO che cercate per la scuola e soprattutto offre tantissime cose, come allenamenti e schede, che a me personalmente sono state MOLTO utili.