Materie

Materie

Di più

Cerca

Knowunity Pro

AI Knowunity

Materie

/

Matematica

/

Aritmetica e algebra

/

Insiemistica e logica

/

Poposizioni semplici e composte con i connettivi e,o,non, enunciati equivalenti,

Come Risolvere Equazioni di Primo e Secondo Grado - Spiegazione Semplice

Vedi

Come Risolvere Equazioni di Primo e Secondo Grado - Spiegazione Semplice
user profile picture

appunti veloci

@appuntiveloci_

·

432 Follower

Segui

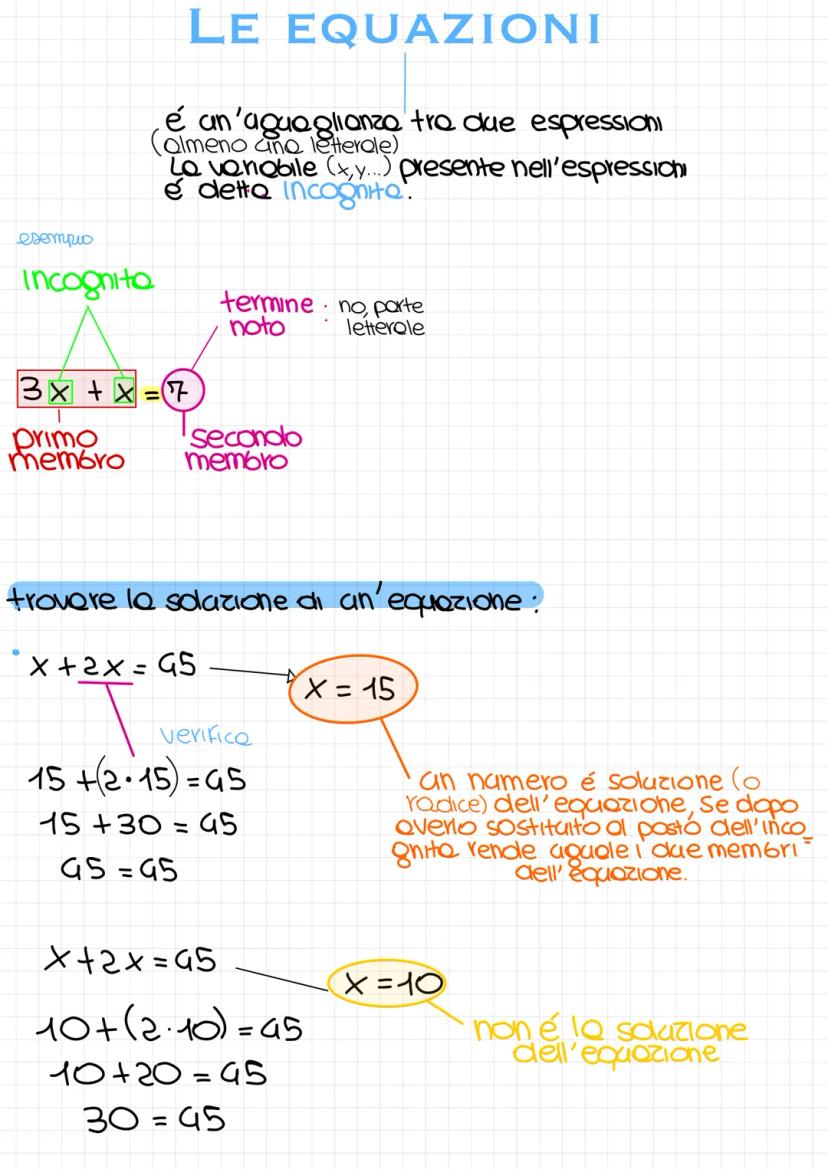
First-degree equations form the foundation of algebraic problem-solving, teaching students how to find unknown values through systematic steps and mathematical reasoning.

• Equations and their solutions are fundamental concepts in algebra, where an equation represents an equality between two expressions containing at least one variable.

• Understanding how to solve first-degree equations involves mastering principles of equivalence, transportation rules, and recognizing different types of solutions.

• The process involves identifying terms, applying mathematical operations systematically, and verifying solutions through substitution.

• Key concepts include equivalent equations, first and second-degree equations, and understanding determinant, indeterminate, and impossible equations.

2/11/2022

40689

<p>Le equazioni rappresentano un'uguaglianza tra due espressioni, con almeno un incognito letterale. L'incognito presente nell'espressione

Vedi

Page 2: Equation Identification and Structure

This page focuses on identifying equations and understanding their structure through practical examples and exercises.

Example: The equation x² = 25 has two solutions: x = +5 and x = -5

Definition: Solving an equation means determining all its possible solutions.

Highlight: The page includes exercises for identifying equations and breaking them down into their components (first member, second member, and unknown).

<p>Le equazioni rappresentano un'uguaglianza tra due espressioni, con almeno un incognito letterale. L'incognito presente nell'espressione

Vedi

Page 3: Principles of Equivalence

This page explains the fundamental principles that govern equivalent equations and how to maintain equation equality.

Definition: Two equations are equivalent when they have exactly the same solutions.

Highlight: First Principle: Adding or subtracting the same expression to both sides of an equation results in an equivalent equation.

Example: 6x + 1 = 2x + 9 is equivalent to 6x + 1 + 3 = 2x + 9 + 3

<p>Le equazioni rappresentano un'uguaglianza tra due espressioni, con almeno un incognito letterale. L'incognito presente nell'espressione

Vedi

Page 4: Rules for Solving Equations

This page outlines the essential rules used in solving equations, including transportation and cancellation rules.

Vocabulary: Transportation Rule (Regola del trasporto) - Terms can be moved from one side to another by changing their sign.

Example: In 3x = 12, the solution is found by dividing both sides by 3, giving x = 4

Highlight: The cancellation rule allows like terms to be combined on the same side of the equation.

<p>Le equazioni rappresentano un'uguaglianza tra due espressioni, con almeno un incognito letterale. L'incognito presente nell'espressione

Vedi

Page 5: Understanding Equation Degrees

This page explains the concept of equation degrees and their classification.

Definition: The degree of an equation is determined by the highest power of the unknown variable.

Example: 5x² + 2 = 7x is a second-degree equation because the highest power of x is 2.

Highlight: First-degree equations have a maximum power of 1 for the unknown variable.

<p>Le equazioni rappresentano un'uguaglianza tra due espressioni, con almeno un incognito letterale. L'incognito presente nell'espressione

Vedi

Page 6: Types of Solutions in First-Degree Equations

This page discusses the three possible types of solutions for first-degree equations.

Definition:

  • Determined equation: Has exactly one solution
  • Indeterminate equation: Has infinitely many solutions
  • Impossible equation: Has no solutions

Example: For ax = b:

  • If a ≠ 0, x = b/a (determined)
  • If a = 0 and b = 0 (indeterminate)
  • If a = 0 and b ≠ 0 (impossible)
<p>Le equazioni rappresentano un'uguaglianza tra due espressioni, con almeno un incognito letterale. L'incognito presente nell'espressione

Vedi

Page 7: Solving Complex Equations

This page demonstrates solving more complex equations through step-by-step examples.

Example: 12x - 3 + 14 = -8x + 5 - 6x is solved by:

  1. Combining like terms
  2. Isolating variables
  3. Solving for x

Highlight: The importance of systematic problem-solving and verification of solutions.

<p>Le equazioni rappresentano un'uguaglianza tra due espressioni, con almeno un incognito letterale. L'incognito presente nell'espressione

Vedi

Page 8: Equivalent Equations

This page concludes with a deeper understanding of equivalent equations.

Definition: Equivalent equations are those that have exactly the same solutions.

Example: 3x = 6 is equivalent to x = 2, as both equations have the same solution.

Highlight: Understanding equivalent equations is crucial for solving complex mathematical problems.

<p>Le equazioni rappresentano un'uguaglianza tra due espressioni, con almeno un incognito letterale. L'incognito presente nell'espressione

Vedi

Page 1: Introduction to Equations

This page introduces the fundamental concept of equations and their components. An equation is defined as an equality between two expressions, with at least one containing a variable (called the unknown).

Definition: An equation is an equality between two expressions where at least one contains a variable.

Vocabulary: The unknown (incognita) is the variable (x, y...) present in the expressions.

Example: In the equation 3x + x = 7, we have:

  • First member: 3x + x
  • Second member: 7
  • Unknown: x

Highlight: A number is a solution (or root) of an equation if, when substituted for the unknown, it makes both sides of the equation equal.

Contenuti simili

Know gli insiemi in matematica thumbnail

245

3689

1ªl

gli insiemi in matematica

appunti di matematica sugli insiemi e sottoinsiemi. i tre modi per rappresentarli, i segni da utilizzare per ogni tipologia e spiegazioni chiare e facili con disegni raffigurativi.

Know Numeri naturali e razionali thumbnail

735

11294

1ªl

Numeri naturali e razionali

Numeri naturali: proprietà operazioni in N, proprietà potenze in N, MCD e mcm. Numeri razionali, numeri decimali, proporzioni e relative proprietà, percentuali.

Know EQUAZIONI thumbnail

5

78

1ªl

EQUAZIONI

regole generali sulle equazioni (di primo grado)

Know Appunti sulle equazioni di primo grado e i principi di equivalenza thumbnail

435

12023

3ªm/1ªl

Appunti sulle equazioni di primo grado e i principi di equivalenza

Appunti completi di teoria con esempi chiari e definizioni

Know equazioni thumbnail

41

934

1ªl/2ªl

equazioni

appunti su equazioni di primo grado

Know i numeri naturali (R), interi (NcZ), razionali (Q) thumbnail

94

2657

1ªm/1ªl

i numeri naturali (R), interi (NcZ), razionali (Q)

i numeri dei gruppi R, N, Z, Q ——>operazioni tra frazioni

Non c'è niente di adatto? Esplorare altre aree tematiche.

Knowunity è l'app per l'istruzione numero 1 in cinque paesi europei

Knowunity è stata inserita in un articolo di Apple ed è costantemente in cima alle classifiche degli app store nella categoria istruzione in Germania, Italia, Polonia, Svizzera e Regno Unito. Unisciti a Knowunity oggi stesso e aiuta milioni di studenti in tutto il mondo.

Ranked #1 Education App

Scarica

Google Play

Scarica

App Store

Knowunity è l'app per l'istruzione numero 1 in cinque paesi europei

4.9+

Valutazione media dell'app

15 M

Studenti che usano Knowunity

#1

Nelle classifiche delle app per l'istruzione in 12 Paesi

950 K+

Studenti che hanno caricato appunti

Non siete ancora sicuri? Guarda cosa dicono gli altri studenti...

Utente iOS

Adoro questa applicazione [...] consiglio Knowunity a tutti!!! Sono passato da un 5 a una 8 con questa app

Stefano S, utente iOS

L'applicazione è molto semplice e ben progettata. Finora ho sempre trovato quello che stavo cercando

Susanna, utente iOS

Adoro questa app ❤️, la uso praticamente sempre quando studio.

Iscriviti per mostrare il contenuto. È gratis!

Accesso a tutti i documenti

Migliora i tuoi voti

Unisciti a milioni di studenti

Iscrivendosi si accettano i Termini di servizio e la Informativa sulla privacy.

Materie

/

Matematica

/

Aritmetica e algebra

/

Insiemistica e logica

/

Poposizioni semplici e composte con i connettivi e,o,non, enunciati equivalenti,

Come Risolvere Equazioni di Primo e Secondo Grado - Spiegazione Semplice

user profile picture

appunti veloci

@appuntiveloci_

·

432 Follower

Segui

First-degree equations form the foundation of algebraic problem-solving, teaching students how to find unknown values through systematic steps and mathematical reasoning.

• Equations and their solutions are fundamental concepts in algebra, where an equation represents an equality between two expressions containing at least one variable.

• Understanding how to solve first-degree equations involves mastering principles of equivalence, transportation rules, and recognizing different types of solutions.

• The process involves identifying terms, applying mathematical operations systematically, and verifying solutions through substitution.

• Key concepts include equivalent equations, first and second-degree equations, and understanding determinant, indeterminate, and impossible equations.

2/11/2022

40689

 

3ªm/1ªl

 

Matematica

2296

<p>Le equazioni rappresentano un'uguaglianza tra due espressioni, con almeno un incognito letterale. L'incognito presente nell'espressione

Page 2: Equation Identification and Structure

This page focuses on identifying equations and understanding their structure through practical examples and exercises.

Example: The equation x² = 25 has two solutions: x = +5 and x = -5

Definition: Solving an equation means determining all its possible solutions.

Highlight: The page includes exercises for identifying equations and breaking them down into their components (first member, second member, and unknown).

<p>Le equazioni rappresentano un'uguaglianza tra due espressioni, con almeno un incognito letterale. L'incognito presente nell'espressione

Page 3: Principles of Equivalence

This page explains the fundamental principles that govern equivalent equations and how to maintain equation equality.

Definition: Two equations are equivalent when they have exactly the same solutions.

Highlight: First Principle: Adding or subtracting the same expression to both sides of an equation results in an equivalent equation.

Example: 6x + 1 = 2x + 9 is equivalent to 6x + 1 + 3 = 2x + 9 + 3

<p>Le equazioni rappresentano un'uguaglianza tra due espressioni, con almeno un incognito letterale. L'incognito presente nell'espressione

Page 4: Rules for Solving Equations

This page outlines the essential rules used in solving equations, including transportation and cancellation rules.

Vocabulary: Transportation Rule (Regola del trasporto) - Terms can be moved from one side to another by changing their sign.

Example: In 3x = 12, the solution is found by dividing both sides by 3, giving x = 4

Highlight: The cancellation rule allows like terms to be combined on the same side of the equation.

<p>Le equazioni rappresentano un'uguaglianza tra due espressioni, con almeno un incognito letterale. L'incognito presente nell'espressione

Page 5: Understanding Equation Degrees

This page explains the concept of equation degrees and their classification.

Definition: The degree of an equation is determined by the highest power of the unknown variable.

Example: 5x² + 2 = 7x is a second-degree equation because the highest power of x is 2.

Highlight: First-degree equations have a maximum power of 1 for the unknown variable.

<p>Le equazioni rappresentano un'uguaglianza tra due espressioni, con almeno un incognito letterale. L'incognito presente nell'espressione

Page 6: Types of Solutions in First-Degree Equations

This page discusses the three possible types of solutions for first-degree equations.

Definition:

  • Determined equation: Has exactly one solution
  • Indeterminate equation: Has infinitely many solutions
  • Impossible equation: Has no solutions

Example: For ax = b:

  • If a ≠ 0, x = b/a (determined)
  • If a = 0 and b = 0 (indeterminate)
  • If a = 0 and b ≠ 0 (impossible)
<p>Le equazioni rappresentano un'uguaglianza tra due espressioni, con almeno un incognito letterale. L'incognito presente nell'espressione

Page 7: Solving Complex Equations

This page demonstrates solving more complex equations through step-by-step examples.

Example: 12x - 3 + 14 = -8x + 5 - 6x is solved by:

  1. Combining like terms
  2. Isolating variables
  3. Solving for x

Highlight: The importance of systematic problem-solving and verification of solutions.

<p>Le equazioni rappresentano un'uguaglianza tra due espressioni, con almeno un incognito letterale. L'incognito presente nell'espressione

Page 8: Equivalent Equations

This page concludes with a deeper understanding of equivalent equations.

Definition: Equivalent equations are those that have exactly the same solutions.

Example: 3x = 6 is equivalent to x = 2, as both equations have the same solution.

Highlight: Understanding equivalent equations is crucial for solving complex mathematical problems.

<p>Le equazioni rappresentano un'uguaglianza tra due espressioni, con almeno un incognito letterale. L'incognito presente nell'espressione

Page 1: Introduction to Equations

This page introduces the fundamental concept of equations and their components. An equation is defined as an equality between two expressions, with at least one containing a variable (called the unknown).

Definition: An equation is an equality between two expressions where at least one contains a variable.

Vocabulary: The unknown (incognita) is the variable (x, y...) present in the expressions.

Example: In the equation 3x + x = 7, we have:

  • First member: 3x + x
  • Second member: 7
  • Unknown: x

Highlight: A number is a solution (or root) of an equation if, when substituted for the unknown, it makes both sides of the equation equal.

Contenuti simili

Matematica - gli insiemi in matematica

appunti di matematica sugli insiemi e sottoinsiemi. i tre modi per rappresentarli, i segni da utilizzare per ogni tipologia e spiegazioni chiare e facili con disegni raffigurativi.

245

3689

5

Know gli insiemi in matematica thumbnail

Matematica - Numeri naturali e razionali

Numeri naturali: proprietà operazioni in N, proprietà potenze in N, MCD e mcm. Numeri razionali, numeri decimali, proporzioni e relative proprietà, percentuali.

735

11294

23

Know Numeri naturali e razionali thumbnail

Matematica - EQUAZIONI

regole generali sulle equazioni (di primo grado)

5

78

0

Know EQUAZIONI thumbnail

Matematica - Appunti sulle equazioni di primo grado e i principi di equivalenza

Appunti completi di teoria con esempi chiari e definizioni

435

12023

2

Know Appunti sulle equazioni di primo grado e i principi di equivalenza thumbnail

Matematica - equazioni

appunti su equazioni di primo grado

41

934

1

Know equazioni thumbnail

Matematica - i numeri naturali (R), interi (NcZ), razionali (Q)

i numeri dei gruppi R, N, Z, Q ——>operazioni tra frazioni

94

2657

0

Know i numeri naturali (R), interi (NcZ), razionali (Q) thumbnail

Non c'è niente di adatto? Esplorare altre aree tematiche.

Knowunity è l'app per l'istruzione numero 1 in cinque paesi europei

Knowunity è stata inserita in un articolo di Apple ed è costantemente in cima alle classifiche degli app store nella categoria istruzione in Germania, Italia, Polonia, Svizzera e Regno Unito. Unisciti a Knowunity oggi stesso e aiuta milioni di studenti in tutto il mondo.

Ranked #1 Education App

Scarica

Google Play

Scarica

App Store

Knowunity è l'app per l'istruzione numero 1 in cinque paesi europei

4.9+

Valutazione media dell'app

15 M

Studenti che usano Knowunity

#1

Nelle classifiche delle app per l'istruzione in 12 Paesi

950 K+

Studenti che hanno caricato appunti

Non siete ancora sicuri? Guarda cosa dicono gli altri studenti...

Utente iOS

Adoro questa applicazione [...] consiglio Knowunity a tutti!!! Sono passato da un 5 a una 8 con questa app

Stefano S, utente iOS

L'applicazione è molto semplice e ben progettata. Finora ho sempre trovato quello che stavo cercando

Susanna, utente iOS

Adoro questa app ❤️, la uso praticamente sempre quando studio.