Piano Cartesiano e Punti

Il piano cartesiano è il tuo sistema di riferimento principale, formato dall'asse x (orizzontale) e dall'asse y (verticale) che si incontrano nell'origine O. I quattro quadranti si numerano in senso antiorario, partendo dal primo in alto a destra.

Tra due punti puoi calcolare facilmente la distanza usando il teorema di Pitagora: d = √$(xb - xa)² + (yb - ya)²$. Immagina un triangolo rettangolo dove la distanza è l'ipotenusa.

Il punto medio M si trova esattamente "a metà strada" tra due punti: xm = $xa + xb$/2 e ym = $ya + yb$/2. Per il baricentro di un triangolo, sommi le tre coordinate e dividi per 3.

Ricorda: Le funzioni creano corrispondenze tra valori x e y. Per trovare intersezioni tra due funzioni, imposta un sistema e risolvi!

La Retta

Le rette hanno due forme principali: implicita $ax + by + c = 0$ e esplicita $y = mx + q$. La forma esplicita è più pratica perché mostra subito le caratteristiche principali.

Il coefficiente angolare m indica la pendenza della retta. Se m > 0 la retta sale, se m < 0 scende, se m = 0 è orizzontale. Due rette sono parallele se hanno stesso m, perpendicolari se m₁ = -1/m₂.

Il termine noto q ti dice dove la retta interseca l'asse y. Esistono rette particolari: quelle parallele all'asse x hanno m = 0, quelle parallele all'asse y non seguono la forma y = mx + q.

Trucco: Per disegnare una retta velocemente, trova due punti sostituendo valori semplici di x nell'equazione!

Formule delle Rette e Circonferenza

Per una retta passante per due punti esiste una sola soluzione, mentre per un punto passano infinite rette (fascio). La distanza punto-retta usa la formula: d = |ax₀ + by₀ + c|/√$a² + b²$.

La circonferenza è l'insieme di punti equidistanti da un centro fisso. L'equazione generale è x² + y² + ax + by + c = 0. Il centro ha coordinate C$-a/2, -b/2$ e il raggio è r = √$α² + β² - c$.

Puoi anche scrivere l'equazione come $x - α$² + $y - β$² = r². Esistono circonferenze particolari: centro nell'origine $a = b = 0$, passante per l'origine $c = 0$, o centrate sugli assi.

Importante: Una circonferenza esiste solo se r ≥ 0. Controlla sempre questo requisito!

Rette e Circonferenze

Una retta rispetto a una circonferenza può essere esterna $distanza centro-retta > raggio$, tangente $distanza = raggio$, o secante (distanza < raggio).

Per trovare le intersezioni, risolvi il sistema tra le due equazioni. Ottieni un'equazione di secondo grado dove il discriminante Δ ti dice tutto: Δ > 0 significa secante, Δ = 0 tangente, Δ < 0 esterna.

Le ascisse dei punti di intersezione sono x₁ e x₂. Per la retta tangente puoi usare le derivate con l'equazione y - y₀ = m$x - x₀$, trovando m attraverso la derivata.

Strategia: Il discriminante è il tuo migliore amico per capire subito la posizione relativa di retta e circonferenza!

La Parabola

La parabola è il luogo geometrico dove ogni punto è equidistante da un fuoco fisso e da una retta detta direttrice. L'equazione è y = ax² + bx + c con a ≠ 0.

Il vertice ha coordinate $-b/2a, -Δ/4a$ e rappresenta il punto minimo o massimo. Il fuoco si trova a $-b/2a, (1-Δ)/4a$. L'asse di simmetria passa per il vertice ed è verticale.

Il coefficiente a determina tutto: il segno indica se la concavità è verso l'alto (a > 0) o il basso (a < 0), mentre il valore assoluto determina quanto è stretta. Esistono anche parabole con asse orizzontale: x = ay² + by + c.

Attenzione: Le parabole non sono funzioni nel senso stretto perché possono associare a una x più valori di y!

Retta-Parabola e Ellisse

Il rapporto retta-parabola segue le stesse regole: Δ < 0 esterna, Δ = 0 tangente, Δ > 0 secante. Una retta parallela all'asse ha sempre una sola intersezione.

L'ellisse è definita dalla somma costante delle distanze da due fuochi fissi. L'equazione con centro nell'origine è x²/a² + y²/b² = 1. Se a² > b² è allungata orizzontalmente.

I fuochi si trovano a $±√(a² - b²), 0$ se orizzontale, i vertici sono a (±a, 0) e (0, ±b). L'eccentricità e = √$a² - b²$/a misura quanto è schiacciata: e = 0 dà una circonferenza, valori vicini a 1 la schiacciano di più.

Curiosità: L'ellisse è una circonferenza "schiacciata" - quando l'eccentricità è zero, i due fuochi coincidono!

Ellisse e Iperbole

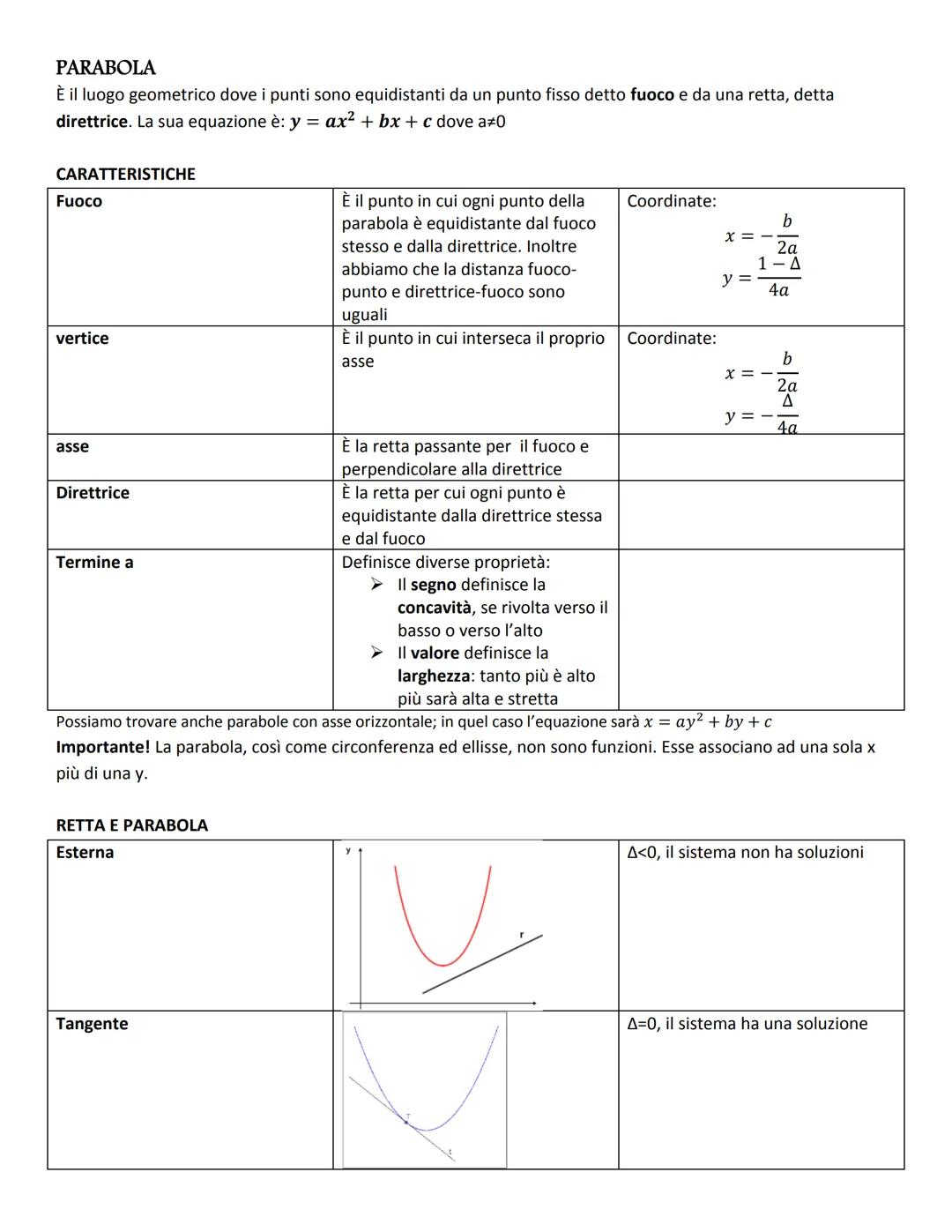
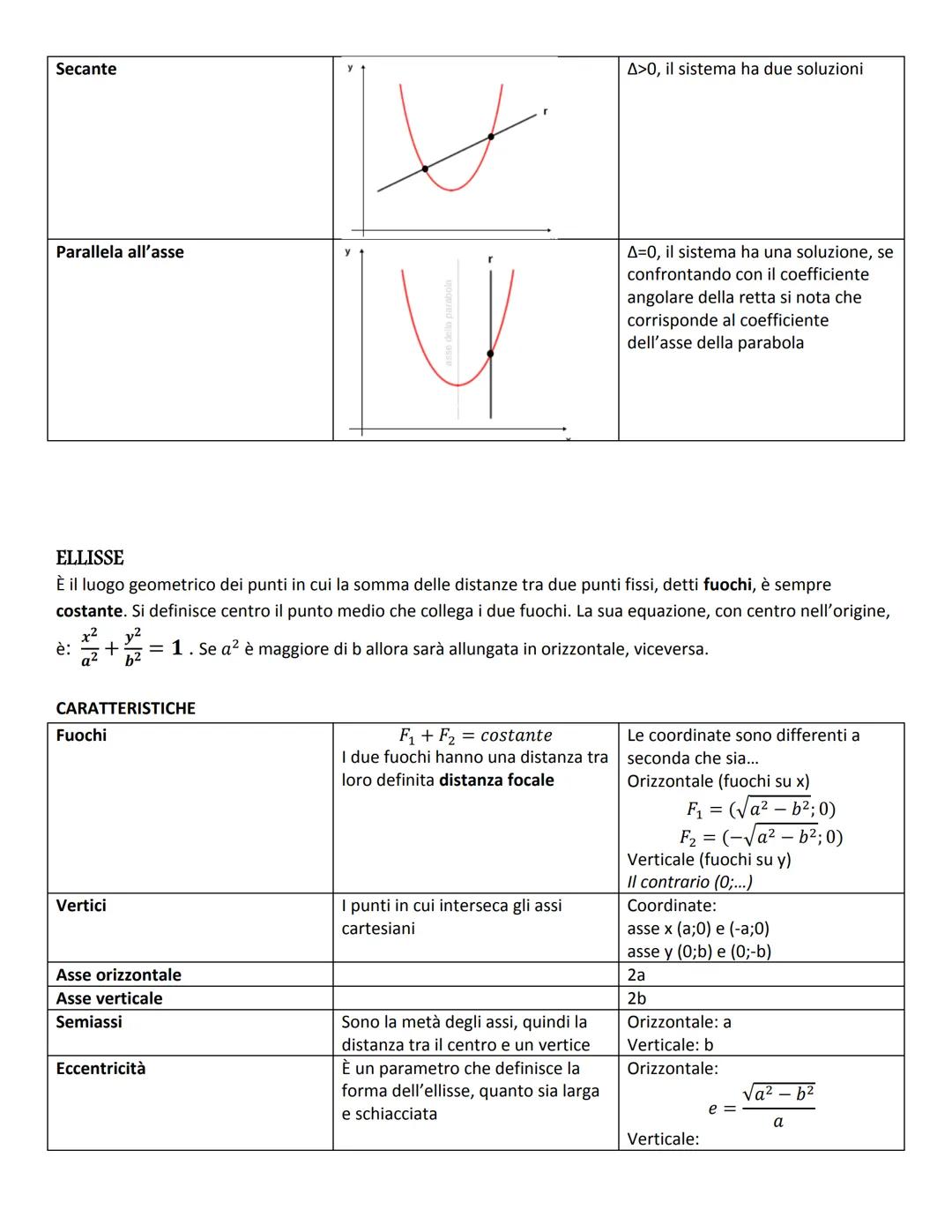
L'ellisse con le rette segue il pattern classico: Δ < 0 esterna, Δ = 0 tangente, Δ > 0 secante.

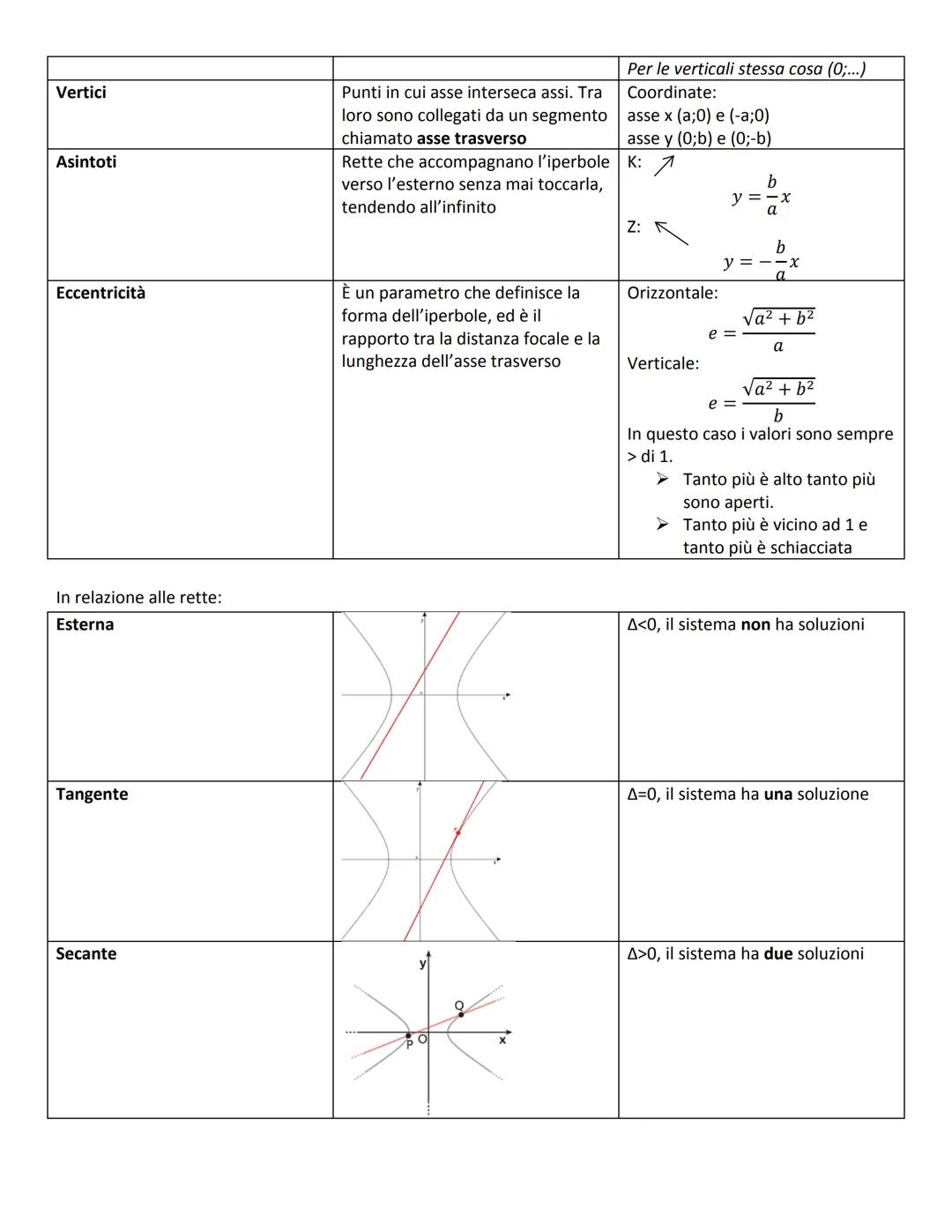
L'iperbole si basa sulla differenza costante delle distanze da due fuochi. Ha due equazioni: x²/a² - y²/b² = 1 (orizzontale) e x²/a² - y²/b² = -1 (verticale).

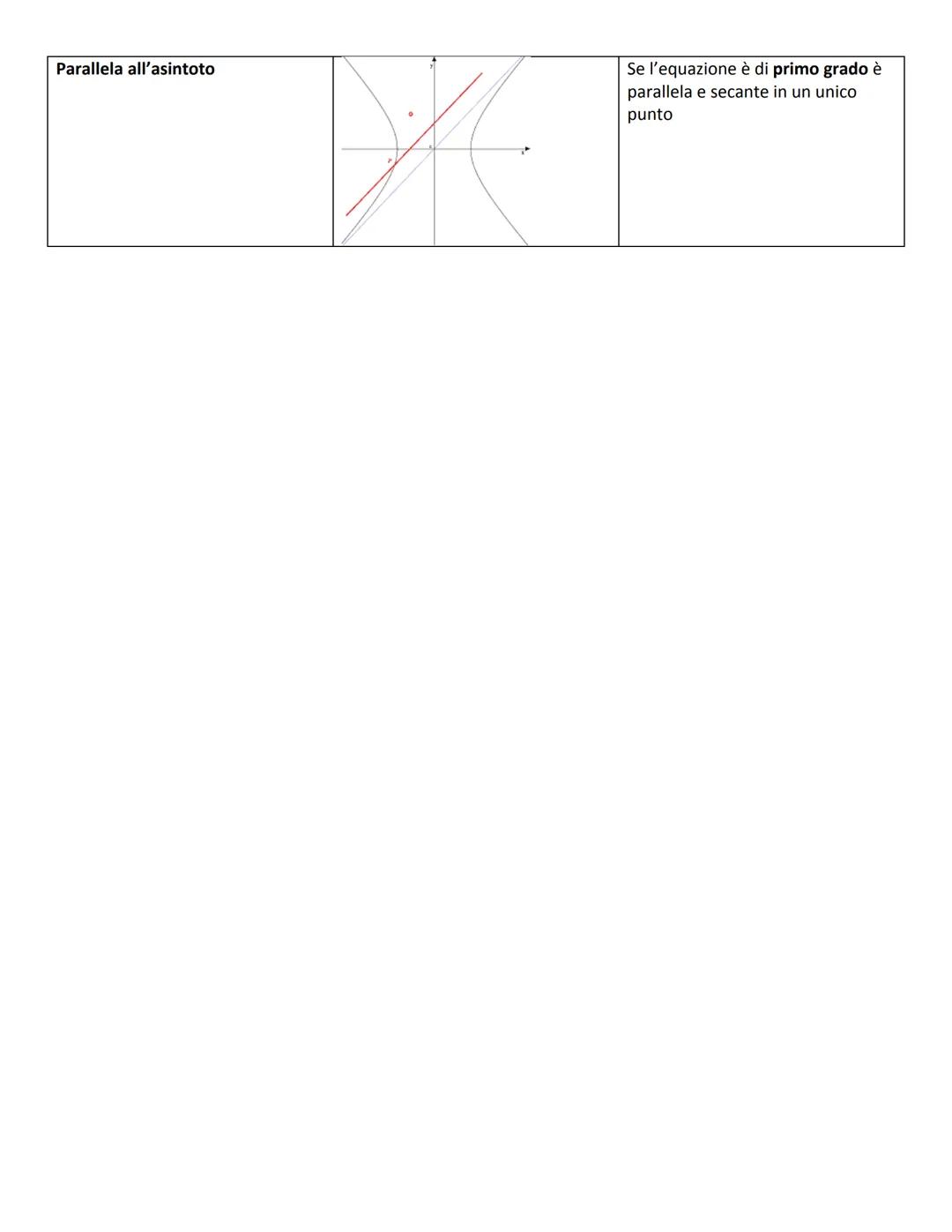
I fuochi sono a $±√(a² + b²), 0$, i vertici a (±a, 0). Gli asintoti sono le rette y = ±$b/a$x che guidano i rami verso l'infinito senza mai toccarli.

L'eccentricità e = √$a² + b²$/a è sempre > 1. Più è alta, più i rami sono aperti; più si avvicina a 1, più l'iperbole è schiacciata.

Visualizza: Gli asintoti sono come binari invisibili che guidano l'iperbole verso l'infinito!

Iperbole e Rette

L'iperbole con le rette mantiene le stesse relazioni: Δ < 0 esterna, Δ = 0 tangente, Δ > 0 secante.

Caso particolare: una retta parallela all'asintoto è sempre secante in un unico punto, creando un'intersezione speciale.

I vertici collegati formano l'asse trasverso, mentre gli asintoti y = ±$b/a$x accompagnano i rami verso l'esterno. L'eccentricità determina l'apertura: valori alti = rami molto aperti, valori vicini a 1 = iperbole schiacciata.

Pro tip: Disegna sempre prima gli asintoti - ti aiutano a capire la forma generale dell'iperbole!

Studio di Funzioni - Introduzione

Lo studio di funzioni segue un percorso metodico in 9 passi che ti porta dal dominio al grafico finale. È come seguire una ricetta: ogni passaggio prepara quello successivo.

Si parte dal dominio (dove esiste la funzione), si controlla se è pari o dispari, si trovano le intersezioni con gli assi, si studia il segno per capire dove la funzione è positiva o negativa.

Gli asintoti sono fondamentali: verticali (limiti che tendono a ±∞), orizzontali (comportamento all'infinito), obliqui (quando non esistono quelli orizzontali).

Metodo: Segui sempre l'ordine dei passaggi - ognuno ti dà informazioni utili per i successivi!

Studio di Funzioni - Derivate e Grafico

La derivata prima ti dice dove la funzione cresce o decresce. Studiando il segno di y' ≥ 0 trovi i punti di massimo e minimo locali.

La derivata seconda rivela la concavità e i flessi. I punti di non derivabilità si classificano in: flesso (limiti infiniti stesso segno), cuspide (limiti infiniti segni opposti), punto angoloso (limiti diversi).

Il teorema di L'Hôpital risolve le forme indeterminate 0/0: deriva numeratore e denominatore separatamente invece di usare i limiti notevoli.

Infine disegni il grafico unendo tutte le informazioni raccolte: dominio, segno, asintoti, crescenza, concavità.

Trucco finale: Il teorema di L'Hôpital ti salva tempo prezioso negli esercizi con forme indeterminate!