La Rivoluzione di Parmenide

Parmenide cambia tutto rispetto ai filosofi che l'hanno preceduto. Mentre i filosofi ionici e pitagorici partivano dall'osservazione del mondo, lui dice che la ragione deve basarsi solo su se stessa, senza fidarsi dell'esperienza dei sensi.

La sua filosofia si basa su un contrasto fondamentale: da una parte c'è l'aletheia (verità), che è stabile e perfetta, dall'altra la doxa (opinione), che cambia continuamente. Per Parmenide esistono due vie: la via della verità che dice "l'essere è e non può non essere", e la via dell'errore che dice "il non essere non è".

Il punto chiave è questo: non si può pensare né esprimere il non essere. Quando i tuoi sensi ti fanno vedere che le cose cambiano o scompaiono, in realtà ti stanno ingannando perché stanno mescolando essere e non essere.

💡 Ricorda: Per Parmenide la ragione è più affidabile dei sensi - quello che vedi non è sempre quello che è veramente!

L'Essere Necessario e le Sue Caratteristiche

Parmenide ci dice di abbandonare i sensi e concentrarci sull'essere necessario, cioè qualcosa che non potrebbe essere diverso da com'è. Nasce così l'ontologia, la ricerca filosofica dell'essere.

Usando la dimostrazione per assurdo, Parmenide dimostra cinque caratteristiche fondamentali dell'essere: è ingenerato (non è mai nato), imperituro (non può morire), unico (non ce ne sono altri), indivisibile (non si può spezzare) e immobile (non cambia mai).

La logica è sempre la stessa: se l'essere avesse caratteristiche opposte, dovremmo ammettere l'esistenza del non essere, che è impossibile. Per esempio, se l'essere potesse finire, da quel momento in poi sarebbe "non essere" - ma questo è assurdo.

💡 Attenzione: L'essere che descrive Parmenide è completamente diverso dal mondo che sperimentiamo ogni giorno!

Il Tentativo di Conciliazione: Luce e Tenebre

Parmenide si rende conto che la sua teoria crea un problema: come spiegare il mondo che vediamo? Prova allora a conciliare ragione e sensi introducendo due principi opposti: luce e tenebra.

Questi principi dovrebbero spiegare come dall'unità dell'essere possa nascere la molteplicità che osserviamo. Entrambi fanno parte dell'essere superiore, ma la loro opposizione genera il mondo delle apparenze.

Tuttavia, questa soluzione rimane problematica. È difficile capire come l'assoluta unità dell'essere possa contenere al suo interno il dualismo di luce e tenebra. Inoltre, anche ammettendo questo dualismo, resta misterioso come da esso nasca la varietà di cose mutevoli che vediamo (inclusi noi stessi).

💡 Problema irrisolto: Parmenide non riesce a spiegare completamente come dall'uno nasca il molteplice!

Zenone: Il Difensore Geniale

Zenone, discepolo di Parmenide, diventa il suo più abile difensore quando la dottrina del maestro viene criticata. Gli oppositori sostengono che è ovvio che esistano molte cose in movimento, ma Zenone risponde con un'arma formidabile: i paradossi.

Il suo metodo è brillante: prende le opinioni basate sull'esperienza come ipotesi di partenza, poi usa la ragione per dimostrare che portano a conclusioni assurde. Quindi conclude che queste opinioni sono false.

I risultati sono chiamati paradossi (dal greco "contro l'opinione comune") proprio perché vanno contro quello che sembra evidente a tutti. La sua strategia è: ipotesi → ragionamento → conclusione assurda → quindi l'ipotesi è falsa.

💡 Geniale: Zenone usa la logica per dimostrare che quello che sembra ovvio è in realtà impossibile!

I Paradossi Contro Molteplicità e Movimento

Zenone costruisce due tipi di argomenti: contro il molteplice e contro il movimento. Nel primo caso, dimostra che se esistessero N cose, nello spazio tra loro dovrebbe esserci qualcosa che le separa (perché il nulla non può esistere). Ma allora le cose sarebbero N+1, poi N+2, e così via all'infinito - assurdo!

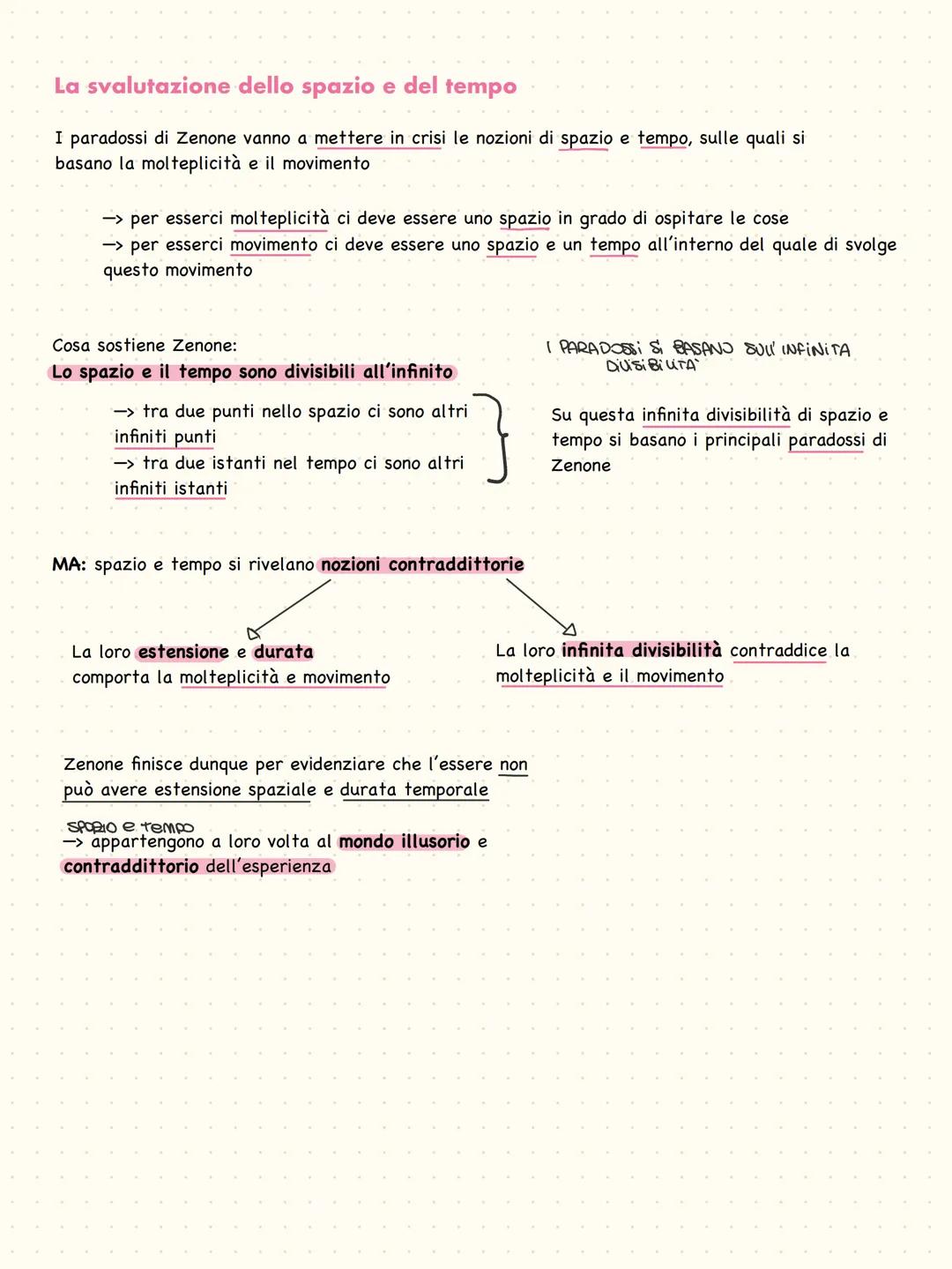
Per il movimento, crea il famoso paradosso dello stadio (o dicotomia). Un corridore che vuole attraversare uno stadio deve prima arrivare a metà, poi a metà della metà rimasta, poi a metà di quella, e così via. Deve percorrere infiniti tratti - quindi non arriverà mai!

Lo stesso principio vale per Achille e la tartaruga: mentre Achille recupera la distanza che lo separa dalla tartaruga, lei ne percorre un'altra piccola. E mentre lui copre quella, lei ne percorre un'altra ancora più piccola, all'infinito.

💡 Mente=esplosa: Questi paradossi hanno fatto impazzire matematici e filosofi per secoli!

La Freccia e l'Illusione del Movimento

Il paradosso della freccia è forse il più affascinante. Zenone dice: in ogni singolo istante, una freccia in volo occupa uno spazio pari alla sua lunghezza, quindi è immobile in quell'istante. Se è immobile in ogni istante, quando si muove?

La sua conclusione è rivoluzionaria: il movimento che osserviamo è un'illusione, come i fotogrammi di un film che creano l'impressione del movimento attraverso una successione di immagini fisse.

Tutti questi paradossi hanno lo stesso obiettivo: dimostrare che le nostre esperienze quotidiane di molteplicità e movimento sono contraddittorie e quindi false. La ragione ci mostra che solo l'essere unico e immobile di Parmenide è reale.

💡 Rivoluzionario: Zenone anticipa di secoli problemi che torneranno nella fisica moderna!

La Critica di Spazio e Tempo

I paradossi di Zenone mettono in crisi i concetti di spazio e tempo, fondamentali per spiegare molteplicità e movimento. Senza spazio non ci sarebbe posto per più cose, senza tempo non ci sarebbe movimento.

Il punto cruciale è l'infinita divisibilità: tra due punti nello spazio ci sono infiniti altri punti, tra due istanti nel tempo ci sono infiniti altri istanti. Su questa proprietà si basano tutti i suoi paradossi principali.

Ma qui nasce la contraddizione: da un lato spazio e tempo permettono molteplicità e movimento, dall'altro la loro infinita divisibilità rende impossibili proprio molteplicità e movimento. Spazio e tempo si rivelano nozioni contraddittorie.

La conclusione di Zenone è radicale: l'essere non può avere né estensione spaziale né durata temporale. Spazio e tempo appartengono al mondo illusorio dell'esperienza, non alla realtà autentica colta dalla ragione.

💡 Conseguenza estrema: Se Zenone ha ragione, tutto quello che sperimentiamo è pura illusione!