Understanding Disequazioni Irrazionali

Disequazioni irrazionali, or irrational inequalities, are a crucial topic in advanced algebra. This page introduces the fundamental concepts and methods for solving these types of inequalities, focusing on those involving square roots.

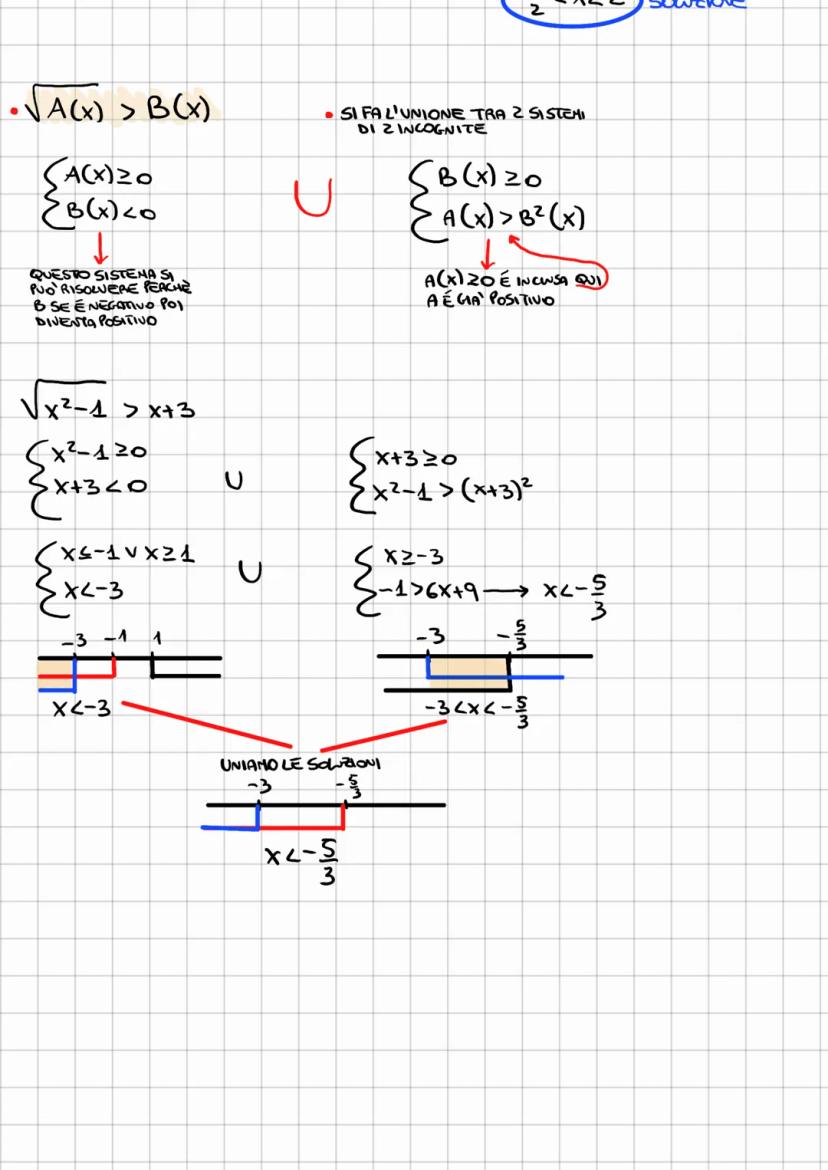
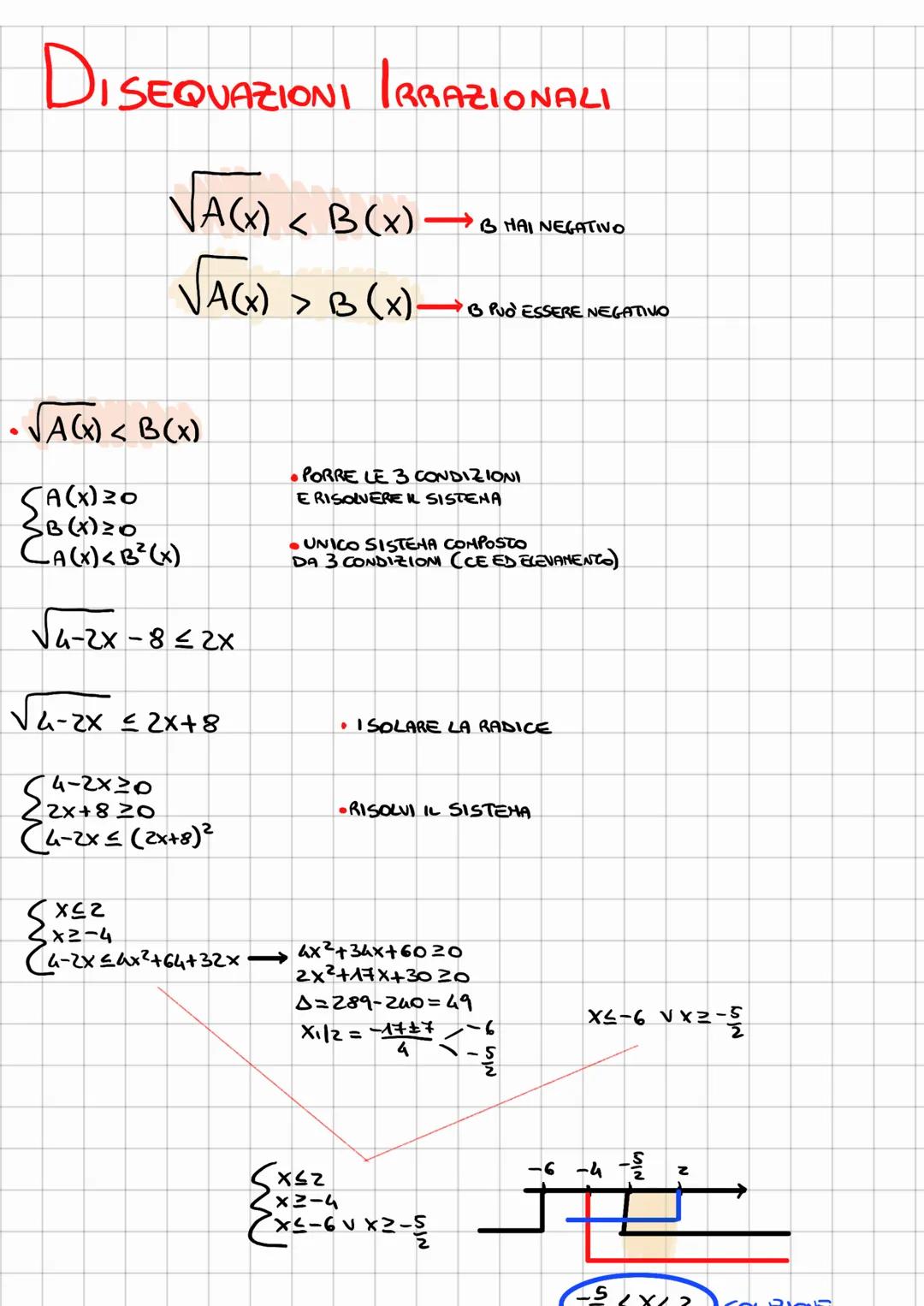
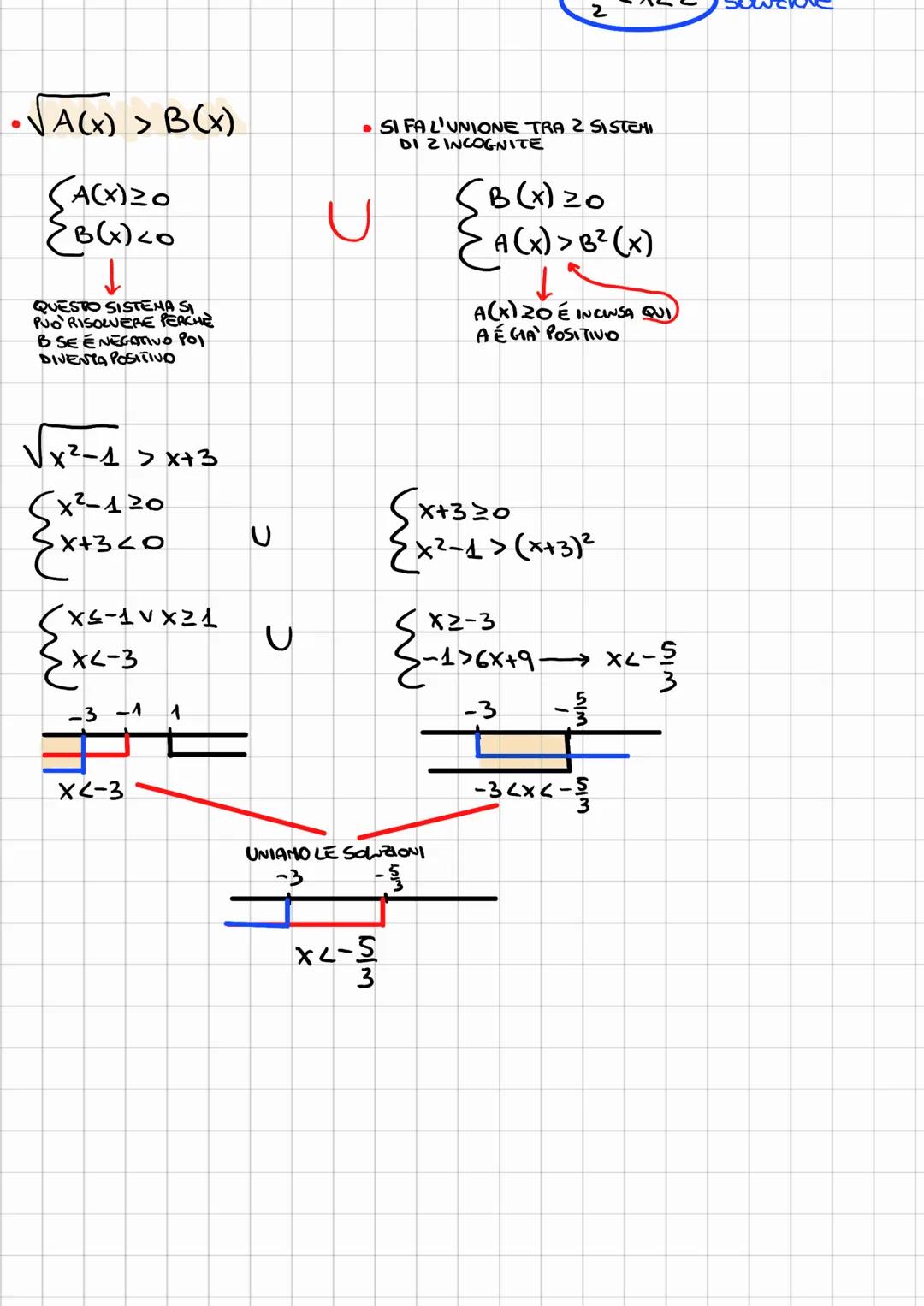
Definition: Disequazioni irrazionali are inequalities that contain radical expressions, typically square roots.

The general form of a simple irrational inequality is √A(x) < B(x) or √A(x) > B(x), where A(x) and B(x) are functions of x.

When solving these inequalities, it's essential to consider the following conditions:

1. The expression under the square root must be non-negative.
2. The inequality must be valid.
3. The solution must satisfy both the original inequality and the domain restrictions.

Example: For the inequality √4-2x-8 ≤ 2x, we must ensure that 4-2x ≥ 0 and solve the squared inequality (4-2x) ≤ (2x+8)².

The solution process typically involves:

1. Isolating the radical on one side of the inequality.
2. Squaring both sides (which may change the direction of the inequality).
3. Solving the resulting quadratic inequality.
4. Checking the domain restrictions and combining the results.

Highlight: It's crucial to remember that squaring both sides of an inequality can introduce extraneous solutions, so always check your answers against the original inequality.

Advanced Techniques for Disequazioni Irrazionali

This page delves deeper into solving more complex disequazioni irrazionali, particularly those involving negative terms on the right side of the inequality.

When dealing with √A(x) > B(x) where B(x) can be negative, we need to consider two separate cases:

1. When B(x) is non-negative
2. When B(x) is negative

Example: For the inequality √x²-1 > x+3, we must solve two systems:

1. {x²-1 ≥ 0, x+3 ≥ 0, x²-1 > (x+3)²}
2. {x²-1 ≥ 0, x+3 < 0}

This approach leads to solving multiple systems of inequalities and then combining the results.

Highlight: The solution to a complex irrational inequality often involves the union of multiple intervals on the real number line.

For inequalities of the form √A(x) < B(x) where B(x) can be negative, we typically solve the system:

{A(x) ≥ 0, B(x) ≥ 0, A(x) < B²(x)}

Vocabulary: The term "dominio" (domain) is crucial in disequazioni irrazionali, as it defines the valid input values for the radical expressions.

These techniques form the basis for solving a wide range of disequazioni irrazionali esercizi, from simple to complex cases.